
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опыт 1.3. Равноускоренное движение
Цель работы: выявление зависимости скорости от времени при равноускоренном движении, ускорения от времени, координаты от времени для равноускоренного движения без начальной скорости. Оборудование: 1. Дорожка с воздушной подушкой. 2. Компрессор. 3. Оптические датчики. 4. Тележка. 5. Компьютер.
Рис. 8. Демонстрация опыта
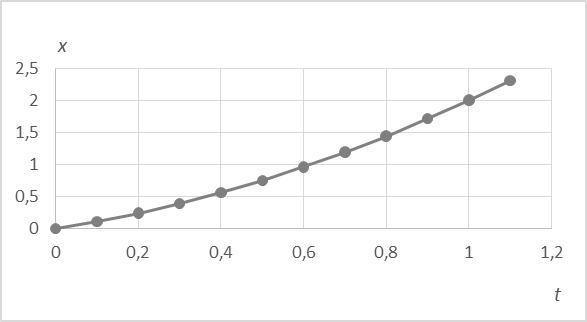
Ход работы На дорожке имеется ножка с микрометрическим винтом, который позволяет устанавливать и точно отсчитывать угол наклона дорожки. Создаем угол наклона 10–2 rad. Теперь мы сможем наблюдать движение тележки по наклонной дорожке, с углом наклона10–2 rad. Это означает что ускорение, которое мы должны получить будет составлять a = g·sinα ≈ 0,01g. Проверим. 1. Теперь на экране наблюдаем зависимость координаты от времени для равноускоренного движения без начальной скорости (параболическая зависимость).
Рис. 9. Зависимость координаты от времени при равноускоренном движении
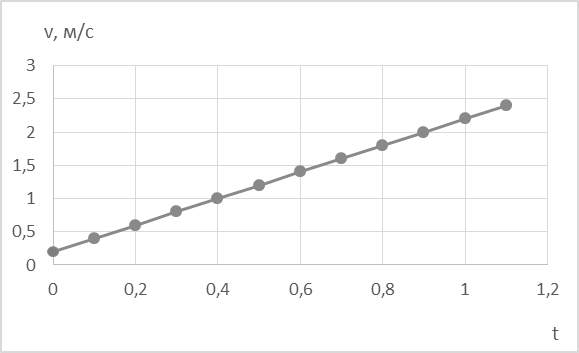
Среднее значение ускорения, вычисленное из этой кривой, составляет 0,096 м/с2, что соответствует тому значению, которое мы ожидали получить. 2. Зависимость скорости от времени при равноускоренном движении. Видно, что зависимость линейная с малым значением начальной скорости, причем среднее ускорение, вычисленное из угла наклона этой кривой, составляет 0,096 м/с2, как и в первом случае.
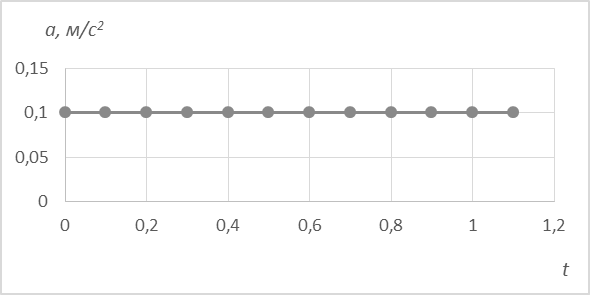
Рис. 10. Зависимость скорости от времени при равноускоренном движении 3. Зависимость ускорения от времени. Ошибки измерения ускорения несколько больше, чем у скорости, поэтому точки относительно среднего ускорения имеют небольшой разброс. Но среднее значение ускорения постоянно, и среднее арифметическое ускорения составляет 0,1 м/с2, что согласуется с теоретическим значением 0,098, полученным нами из наклона дорожки в пределах ошибок.
Рис. 11. Зависимость ускорения от времени при равноускоренном движении
Вывод: продемонстрировано равноускоренное движение, выявлены все требуемые зависимости.
Опыт 1.4 Падение тел Цель работы: рассмотреть независимость времени падения тел от величины горизонтальных составляющих и начальной скорости. Оборудование: 1. Стальные шары. 2. Горка. 3. Электромагнит.
Рис.12. Демонстрация опыта
Ход работы 1. Один шар скатывается с горки, приобретает некоторую скорость в горизонтальном направлении 2. Шар начинает падение одновременно со вторым шаром, покоившимся в точке на линии, проведенной вдоль начальной скорости первого шара. Одновременность начала падения шаров обеспечивается тем, что первый шар в конце горки размыкает контакт в цепи питания электромагнита, удерживающего второй шар. 3. Далее шары, двигаясь по разным траекториям – по параболе и по прямой, но с одинаковым ускорением свободного падения g и одинаковой нулевой начальной скоростью в вертикальном направлении, оказываются одновременно в одном месте, то есть сталкиваются. Вывод: рассмотрели падение тел и узнали о независимости времени падения тел от величины горизонтальных составляющих и начальной скорости.
Опыт 1.5. Сложение движений Цель работы: изучить сложение движений на примере вращающегося диска с наблюдателями. Оборудование: 1. Вращающийся диск. 2. Мел.
Рис. 13. Демонстрация опыта
Ход работы Траектория тела зависит от того, в какой системе отсчета сидит наблюдатель. 1. Пусть будут два наблюдателя: один сидит на диске, а второй на неподвижной раме. 2. Если мы будем двигать кусок мела по диаметру, пока диск неподвижен, то траектория куска мела при его равномерном движении получается в виде прямой линии. 3. Но если наш диск будет вращаться, то траектория для неподвижного наблюдателя по-прежнему будет являться прямой линией, а для движущегося наблюдателя это будет уже совершенно другая линия – спираль Архимеда. Для неподвижного наблюдателя мел по-прежнему двигался по прямой линии, а для наблюдателя, сидящего на диске, мел совершил замысловатую кривую. Она получается в результате сложения двух движений: равномерного движения по радиусу вращающегося диска и равномерного вращения вокруг оси диска Вывод: рассмотрели сложение движений на примере вращающегося диска с двумя наблюдателями. Узнали о спирали Архимеда, которая получается в результате сложения двух движений.
Недостаточно кинематически характеризировать движениеточки формой траектории, путем S и радиус-вектором
Пусть материальная точка движется по криволинейной траектории. Вектор перемещения
Известно, что:
Для нахождения пути, пройденного телом за промежуток времени Δt, надо найти интеграл:
Скорость механического движения в большинстве случаев не остается постоянной, а меняется со временем либо по величине, либо по направлению, либо по величине и направлению одновременно. Приращение скорости
среднее ускорение
Используя предыдущие рассуждения, получим мгновенное ускорение:
Ускорение – физическая величина, характеризующая быстроту изменения скорости. Ускорение – вектор, равный производной от вектора скорости по времени и совпадающий по направлению с вектором изменения скорости dv за малый интервал времени dt. Легко показать, что
Зная кинематические уравнения движения, можно по аналогии получить:
а для модулей векторов скорости и ускорения:
Криволинейное движение В общем случае криволинейного неравномерного движения скорость изменяется как по величине, так и по направлению. Полное ускорение, которым обладает движущаяся точка, определяет оба вида изменения скорости. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости направлен всегда по касательной к траектории. Найдем вектор изменения скорости:
где Δv характеризует изменение скорости и по величине и направлению. Разложим Δv на две составляющие:
Относительное движение Системы отсчета можно связать как с неподвижными телами отсчета, так и с движущимися. Движение тела в подвижной системе – относительное движение. Движение тела в неподвижной системе – абсолютное движение. Движение тела относительно неподвижной системы отсчета, которым бы оно обладало, будучи жестко связанным одной из точек подвижной системы отсчета, называется переносным движением.
Преобразования ГАЛИЛЕЯ
Зная, что
Уравнения (27) и (28) в векторной записи в общем случае:
Из уравнения (30) следует, что ускорение одного и того же тела в каждый момент времени одинаково во всех системах отсчета, движущихся относительно друг друга равномерно и прямолинейно. Системы отсчета, движущиеся относительно неподвижной равномерно и прямолинейно, называются инерциальными. Следовательно, инерциальные системы отсчета образуют замкнутую систему. В некоторых задачах за инерциальные могут быть приняты системы, связанные с Землей или телами, движущимися, движущимися относительно Земли равномерно и прямолинейно. Равенство (7) выражает механический принцип относительности.
Уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой. Введение сил инерции дает возможность описывать движение тел в любых системах отсчета. Силы инерции не являются силами воздействия (упругие, гравитационные, трения), они обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления. Силы инерции – фиктивные силы.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 799; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.96.135 (0.021 с.) |



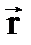 , надо указать быстроту перемещения.
, надо указать быстроту перемещения.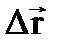 представляет приращение радиус-вектора
представляет приращение радиус-вектора 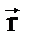 за время Δt:
за время Δt: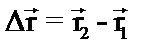 . (9)
. (9)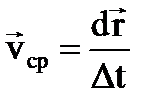 , (10)
где
, (10)
где 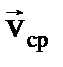 – средняя скорость движения.
Вектор
– средняя скорость движения.
Вектор 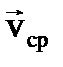 совпадает по направлению с
совпадает по направлению с 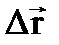 .
Мгновенная скорость, т.е. скорость в данный момент времени:
.
Мгновенная скорость, т.е. скорость в данный момент времени:
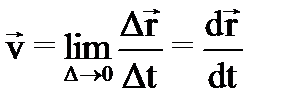 . (11)
. (11)
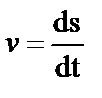 . (12)
. (12)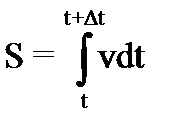 . (13)
. (13)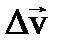 :
: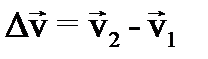 , (14)
, (14)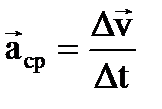 . (15)
. (15)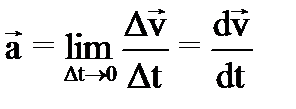 . (16)
. (16)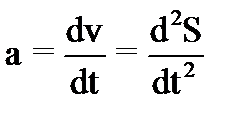 . (17)
. (17)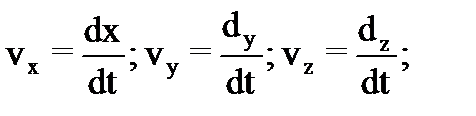 (18)
(18)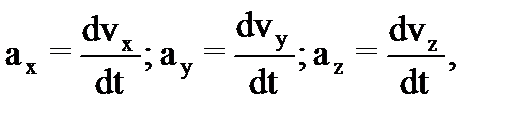 (19)
(19)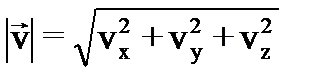 , (20)
, (20)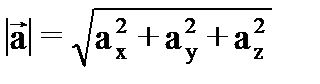 . (21)
. (21)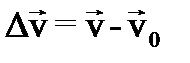 , (22)
, (22)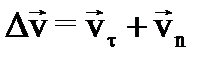 (23)
Учитывая, что
(23)
Учитывая, что
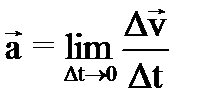 ,
имеем
,
имеем
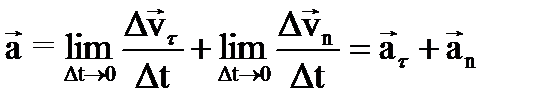 .
.
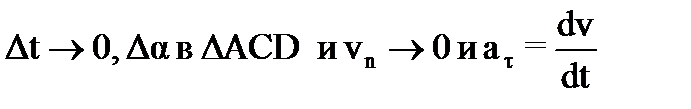 ;
2) при
;
2) при 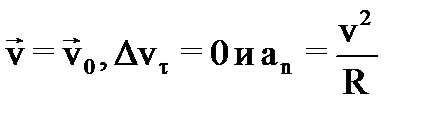 ;
3) модуль полного ускорения определяется как
;
3) модуль полного ускорения определяется как
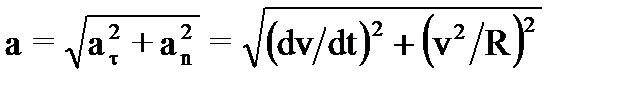 . (24)
Так как векторы ускорений
. (24)
Так как векторы ускорений 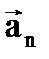 и
и 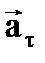 взаимно перпендикулярны, то:
взаимно перпендикулярны, то:
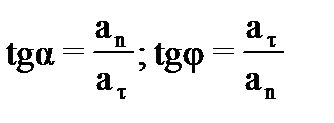 . (25)
Угол j определяет направление полного ускорения.
. (25)
Угол j определяет направление полного ускорения.
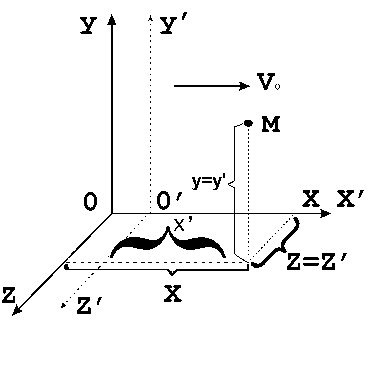 Рис. 17. Относительность движения
Рис. 17. Относительность движения
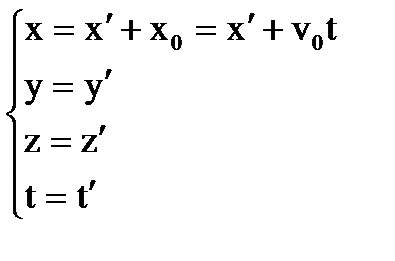 (26)
(26)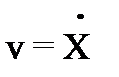 и
и 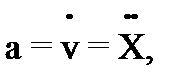 имеем:
имеем: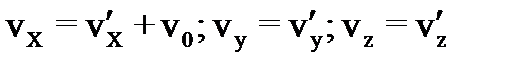 , (27)
, (27)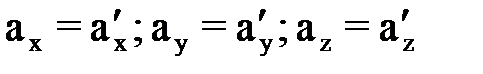 . (28)
. (28)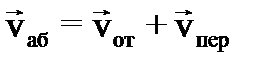 , (29)
, (29)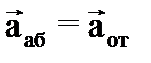 . (30)
. (30)


