
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление. Распределение давления в покоящихся жидкостях и газахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В обычных условиях жидкости не оказывают сопротивления изменению формы, но сохраняют свой объем. Газы не сохраняют ни формы, ни объема.
Для изменения объема жидкости или газа требуются внешние силы, при этом в жидкости и газе возникают упругие силы. Эти упругие свойства характеризуются величиной – давлением. Давление по определению равно:
Давление – скаляр, так как его величина не зависит от ориентации площадки, к которой отнесено давление. Давление в газах определяется аналогично. Единицы давления: СИ: Н/м2 (Па – Паскаль). Внесистемные единицы: 1 мм рт.ст. = 133 Па. 1 атм (физич.) = 1,01·105 Па = 1,033 ат (техн.).
Закон Паскаля используется в гидравлических прессах. Определим давление внутри весомой жидкости.
P0S + ρhSg – PS = 0.
P = P0 + ρgh (171) – гидростатическое уравнение Pr = ρgh называется гидростатическим давлением, создаваемым весом столба жидкости высотой h. Следствия:
Барометрическая формула:
Давление убывает с высотой по показательной функции, обращаясь в ноль только на бесконечно большой высоте.
2. Плавание тел. Закон Архимеда
Опыт 8.1. Ведерко Архимеда Цель работы: проверить справедливость закона Архимеда при помощи ведерка Оборудование: 1. Ведерко Архимеда. 2. Весы. 3. Вода.
Рис. 129. Установка для опыта Ход работы Справедливость закона Архимеда может быть легко показана при помощи так называемого ведерка Архимеда. 1. На уравновешенных весах находится ведерко Архимеда, которое представляет собой два цилиндра, плотно пригнанных друг к другу. 2. Подвесим эти цилиндры друг за другом на весах, не погружая их в жидкость. 3. Затем заполним стакан жидкостью. Равновесие весов за счет появления выталкивающей силы нарушается, то есть погружаемый в воду цилиндр, объем которого равен внутреннему объему верхнего цилиндра, теряет в весе. 4. Теперь заполним той же водой верхний цилиндр. Мы видим, что равновесие весов восстанавливается. Таким образом, тело, погруженное в жидкость, теряет в своем весе ровно столько, сколько весит жидкость в объеме, равном объему этого тела. Это закон Архимеда.
Вывод: с помощью ведерка Архимеда, проверили справедливость закона Архимеда. Тело, погруженное в жидкость, теряет в своем весе ровно столько, сколько весит жидкость в объеме, равном объему этого тела.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.93 (0.01 с.) |

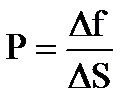 .
.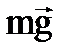
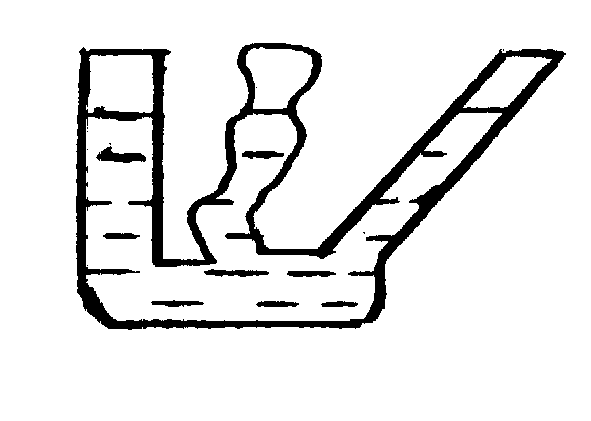 Рис. 127
Рис. 127
 Рис. 128
Рис. 128
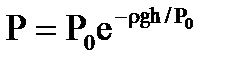 (172)
(172)



