
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальний вигляд платіжної матриціСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Скінченна парна гра з нульовою сумою називається також матричною грою, оскільки їй у відповідність можна поставити матрицю. З вигляду платіжної матриці можна зробити висновок, які стратегії є свідомо невигідними. Це ті стратегії, для яких кожен з елементів відповідного рядка матриці менший або дорівнює відповідним елементам іншого будь-якого рядка. Справді, кожен елемент матриці — це виграш гравця А, і якщо для якої-небудь стратегії (рядка) всі виграші менші від виграшів іншої стратегії, зрозуміло, що перша стратегія менш вигідна, ніж друга. Така операція відбраковування явно невигідних стратегій називається мажоруванням. Якщо задачу зведено до матричної форми, то можна порушувати питання про пошук оптимальних стратегій. Насамперед, введемо поняття верхньої та нижньої ціни гри. Нижньою ціною гри називається елемент матриці, для якого виконується умова:
Нижня ціна гри показує, що хоч би яку стратегію застосовував гравець В, гравець А гарантує собі виграш, не менший за а. Верхньою ціною гри називається елемент, що задовольняє умову:
Верхня ціна гри гарантує для гравця В, що гравець А не отримає виграш, більший за β. Точка (елемент) матриці, для якої виконується умова
називається сідловою точкою. У цій точці найбільший з мінімальних виграшів гравця А точно дорівнює найменшому з максимальних програшів гравця В, тобто мінімум у якому-небудь рядку матриці збігається з максимумом у будь-якому стовпці. Сідлова точка є розв’язком матричної гри, в якій мінімаксним стратегіям притаманна стійкість [4]. Під час аналізу платіжної матриці можливі два випадки оцінювання вибору [31]: Випадок 1. Платіжна матриця має сідлову точку. Оскільки ми прийняли умову максимальної розумності гравців, то саме ці рядок та стовпець і являють собою оптимальні стратегії гравців. За умови використання одним із гравців оптимальної стратегії іншому гравцю невигідно відступати від своєї оптимальної стратегії, тобто стратегії, що відповідають сідловій точці, є найбільш вигідними для обох гравців. Метод вибору стратегій на основі сідлової точки називається «принципом мінімаксу», який інтерпретується так: чини так, аби за найгіршої для тебе поведінки супротивника отримати максимальний виграш.
Випадок 2. Платіжна матриця не має сідлової точки. Це, звичайно, поширеніший випадок. У цій ситуації теорія пропонує керуватися так званими мішаними стратегіями, тобто тими стратегіями, в яких випадковим чином чергуються особисті стратегії. Цей метод широко використовується на інтуїтивному рівні. Наприклад, продавець, не знаючи, який з товарів матиме попит, прагне по можливості урізноманітнити асортимент; оптимальний портфель цінних паперів складають з паперів різних видів. Точний метод знаходження оптимальної мішаної стратегії зводиться до задачі лінійного програмування і, хоча й не є дуже складним, досить трудомісткий. Існують спеціальні комп’ютерні програми, що реалізують цей метод. Утеорії ігор мішана стратегія — модель мінливої, гнучкої тактики, коли жоден із гравців не знає, як поведе себе противник у даній ситуації.Мішана стратегія гравця — це застосування всіх його чистих стратегій у разі багаторазового повторення гри в тих самих умовах із заданими ймовірностями. У мови застосування мішаних стратегій: гра без сідлової точки; гравці використовують випадкове поєднання чистих стратегій із заданими ймовірностями; гра багаторазово повторюється в подібних умовах; під час кожного з ходів жоден гравець не інформований про вибір стратегії іншим гравцем; допускається осереднення результатів ігор. Коли гравець приймає рішення, керуючись чистою стратегією, то з усіх своїх варіантів він обере один, який і використає. Якщо ж він діє відповідно до цієї стратегії, то розраховує (або апріорно задається) ймовірності кожного з можливих рішень [14]. Гравець А розраховує ймовірності Чисті стратегії гравця є єдино можливими неспільними подіями. У матричній грі, знаючи платіжну матрицю, можна визначити за заданих векторів p і q середній виграш (математичне сподівання) гравця А:
де p і q — вектори відповідних імовірностей;
Через застосування своїх мішаних стратегій гравець A намагається максимально збільшити свій середній виграш, а гравець B — довести цей ефект до мінімально можливого значення. Гравець A прагне досягти виконання умови:
Гравець В домагається виконання іншої умови:
Позначимо
Ціна гри γ — середній виграш гравця А за використання обома гравцями мішаних стратегій. Отже, розв’язком матричної гри є: Мішані стратегії будуть оптимальними (
За вибору оптимальних стратегій гравцю А завжди буде гарантований середній виграш, не менший, ніж ціна гри, за будь-якої фіксованої стратегії гравця В (а для гравця В навпаки). Активними стратегіями гравців А і В називають стратегії, що входять до складу оптимальних мішаних стратегій відповідних гравців з імовірностями, відмінними від нуля. Отже, до складу оптимальних мішаних стратегій гравців можуть входити не всі апріорі задані їхні стратегії. Перші роботи з теорії ігор характеризувалися спрощеністю припущень та високим ступенем формальної абстракції, що робило їх малопридатними для практичного використання. Але за останні 10—15 років становище змінилося. На сучасному етапі застосування методів теорії ігор можливе для обґрунтування рішень щодо проведення принципової цінової політики, виходу на ринок, створення спільних підприємств, корпорацій, розрахунку часу розробки нової продукції, формування та розвитку внутрішньофірмових культур. Положення даної теорії в принципі можна використовувати для всіх видів рішень, якщо на їх прийняття впливають інші суб’єкти (ринкові конкуренти, постачальники, провідні клієнти, працівники). Але існують певні межі застосування аналітичного інструментарію теорії ігор [49]. Він може бути використаний лише за умови отримання додаткової інформації в таких випадках: · коли в підприємств склалися різні уявлення про гру, в якій вони беруть участь, чи коли в них бракує інформованості відносно можливостей один одного (наприклад, може мати місце неясна інформація про платежі конкурента, структуру витрат); якщо нестача інформації стосується надто важливих питань, то можна оперувати зіставленням подібних випадків з урахуванням визначених розходжень; · за безлічі ситуацій рівноваги; ця проблема може виникнути навіть у ході простих ігор з одночасним вибором стратегічних рішень; · якщо ситуація прийняття стратегічних рішень дуже складна, то гравці часто не можуть вибрати кращі для себе варіанти (наприклад, на ринок у різний час можуть вийти кілька підприємств або реакція вже діючих там підприємств може виявитися більш складною, ніж має бути). Експериментально доведено, що в разі розширення гри до десяти і більш етапів гравці вже не в змозі скористатися відповідними алгоритмами і далі грати з рівноважними стратегіями. Таким чином, за допомогою теорії ігор суб’єкт господарювання дістає можливість передбачити дії (ходи) своїх партнерів і конкурентів. Але через складність дану теорію доречно використовувати тільки для прийняття одиничних, принципово важливих господарських рішень. Оскільки знаходження оптимальних стратегій методами класичної теорії ігор вимагає здебільшого застосування методів імітаційного моделювання, розглянемо на прикладах більш прості випадки.
Дано платіжну матрицю (табл. 1). Спростити матрицю за рахунок відбраковування явно невигідних стратегій [31]. Таблиця 1 ПЛАТІЖНА МАТРИЦЯ
Розв’язання У матриці всі елементи стратегії А 3 менші за відповідні елементи стратегії А 1. Отже, стратегія А 3 є невигідною, порівнюючи зі стратегією А 1, і може бути відкинута. Так само елементи стратегії А 5 менші за відповідні елементи стратегії А 2. Тому і стратегія А 2 може бути відкинута. Тож, платіжну матрицю в спрощеному вигляді зображено в табл. 2. Таблиця 2 ПЕРЕТВОРЕНА ПЛАТІЖНА МАТРИЦЯ
Знайти сідлову точку в грі, що характеризується платіжною матрицею, даною в таблиці. Таблиця ПЛАТІЖНА МАТРИЦЯ
Розв’язання α = max(– 50; – 60; 30; – 60) = 30; β = (70; 30; 40; 60; 40) = 30; 30 = 30. Висновок: точка на перетині стратегій А 3 і В 2 є сідловою точкою.
Підприємці А та В конкурують на ринку збуту продукції. Кожен з них виробляє два види товарів: А — товари виду а 1 і а 2; В — товари виду b 1 і b 2. Товари а 1 і а 2 та товари b 1 і b 2 мають приблизно однакові властивості. Ціна за одиницю товару а 1 і b 1 становить 10 г. о., ціна за одиницю товару а 2 становить 20 г. о., b 2 — 5 г. о. Ринок насичений цими товарами та розподілений так: а 1: b 1 → 1: 1, а 2: b 2 → 1: 4. Щодня на ринку продається по 2000 одиниць товару а 1 і b 1, 1000 одиниць а 2, 4000 одиниць b 2. Biд продажу кожної одиниці продукції а 1 і b 1 отримується прибуток 2 г. о., а а 2 і b 2 — 4 г. о. Підприємець А бажає посісти провідне місце на ринку. Для цього в нього є такі можливості: знизити ціну на виріб а 1 до 9,5 г. о. — у цьому випадку він витисне з ринку товар b 1 (A 1); знизити ціну на виріб а 2 до 19 г. о. — у цьому випадку, якщо ціна b 2, то ринок на товари а 2 і b 2 розподілиться в співвідношенні 2: 3 (А 2). Проаналізувавши ситуацію, підприємець А дійшов висновку, що В може відповісти так: нічого не робити у відповідь (В1); знизити ціну на виріб b1 до 9,5 г. о. (В2); збільшити обсяг продажу виробу b2 на 25 %, тоді В повністю витисне А з ринку виробів b2 (В3). Передбачається, що у разі потреби кожен з підприємців може наситити ринок товарами. Необхідно скласти платіжну матрицю для підприємця А [31].
Розв’язання Домовимося можливості підприємців, позначені відповідними літерами з індексами, називати їхніми стратегіями. У даному випадку платіжна матриця може мати розмір 2 · 3, оскільки в А є дві стратегії, а у В — три. Елементи матриці будемо обчислювати як виграш у новій ситуації, порівняно зі старою, а саме: елемент матриці = повний прибуток – старий прибуток. Таким чином, маємо — а 11: А знижує ціну на виріб а 1, а В не вживає жодних заходів. У цьому випадку А може продати не 2000, а 4000 виробів а 1. а 11 = 4000 · 1,5 – 2000 · 2 = 2000. — а 12: А знижує ціну на виріб а 1, а В знижує ціну на виріб b 1 до 9,5 г. о. а 12 = – 2000 · 20 + 2000 · 1,5 = – 1000. — а 13: А знижує ціну на виріб а 1 і продає не 2000, а 4000 виробів а 1, але не продає жодного виробу а 2, тому що весь ринок з а 2 захоплює В. а 13 = 40 000 · 1,5 – 2000 · 2 – 1000 · 4 = – 2000. — а 21: А знижує ціну на виріб а 2, і В не вживає жодних заходів. У цьому випадку А продає не 1000, а 2000 виробів а 2. а 21 = 2000 · 3 – 1000 · 4 = 2000. — а 22: А знижує ціну на виріб а 2, а В знижує ціну на виріб b 1, у цьому випадку А продає не 1000, а 2000 виробів а 2, але В повністю витісняє А з ринку товару а 1. а 22 = 2000 · 3 – 1000 · 4 – 1000 · 2 = 0. — а 23: А знижує ціну на виріб а 2, а В збільшує випуск виробів b 2 на 1000 одиниць і зовсім витісняє А з ринку виробів а 2. а 23 = 0 – 1000 · 4 = – 40 000. Платіжна матриця, розрахована таким чином, набуває вигляду матриці, представленої в таблиці. Таблиця ПЛАТІЖНА МАТРИЦЯ
Скласти платіжну матрицю — найчастіше розв’язати саму задачу. Ніякого подальшого розв’язку не потрібно. Висновок: аналіз матриці показує, що А виграє тільки в тому випадку, якщо В не реалізує своїх стратегій. У даному випадку А не слід застосовувати жодної з аналізованих ним стратегії. Це не означає, що в А немає оптимальних стратегій. Просто їх не виявилося серед тих, що перевірялися.
Господарський ризик — це специфічна характеристика діяльності, пов’язана з подоланням невизначеності в господарській ситуації, в якій не виключається ймовірність виникнення не- Першопричиною, необхідною умовою виникнення підприємницьких ризиків виступає невизначеність результатів діяльності. Ризику, як одній з найбільш складних категорій, пов’язаних з результативністю господарської діяльності, притаманні такіриси, як: імовірнісна природа; економічна природа; альтернативність; невизначеність результатів; коливання рівня ризику; постійність. Ризик вважається об’єктивно-суб’єктивною категорією. Для розуміння природи підприємницького ризику фундаментальне значення має зв’язок ризику та прибутку. Проблема взаємовідношення даних категорій — одна з ключових концепцій у виробничо-господарській діяльності підприємств.
Появу підприємницьких ризиків зумовлюють численні фактори — умови, які можуть викликати та спричинити невизначеність результатів здійснення господарської діяльності. Основними критеріями визначення факторів підприємницького ризику виступають: джерело виникнення (зовнішні та внутрішні фактори); ступінь впливу (фактори прямої та непрямої дії); сфера господарської діяльності підприємства. В економічній літературі виділяють такі функції ризику, як: інноваційна, регулятивна, захисна, компенсаційна, соціально-економічна й аналітична. Науково обґрунтована класифікація ризику чітко визначає місце конкретного виду ризику в їх загальній системі та створює умови для ефективного застосування відповідних методів, прийомів управління ризиком. В економічній літературі пропонуються різноманітні способи класифікації ризиків, але не існує однозначного підходу до певних класифікаційних ознак. Обґрунтування рішень в умовах ризику здійснюється за допомогою теорії ігор та теорії (критеріїв) прийняття рішень в умовах ризику. Теорія ігор як розділ дослідження операцій являє собою теорію математичних моделей прийняття оптимальних рішень в умовах конфлікту декількох сторін, що мають різні (протилежні) інтереси. Гра — спрощена математична модель певної конфліктної ситуації. Мета теорії ігор — визначити таку стратегію гравця, за якої шанси на виграш були б найбільшими. Критерії обґрунтування господарських рішень в умовах ризику здійснюються за умов відомих імовірностей несприятливих наслідків подібних подій. Ці ймовірності можуть бути визначені на підставі або статистичних даних, або експертних оцінок.
6.1. Проектний ризик та прийняття Інвестиційні рішення — рішення щодо вкладення (інвестування) коштів в активи у певний момент часу для одержання прибутку в майбутньому. Вони являють собою акти діяльності ОПР з обґрунтованого вкладення фінансових та реальних (матеріальних та нематеріальних) інвестицій. Інвестиційний проект (ІП) — план (програма) заходів, пов’язаних зі здійсненням капітальних вкладень для їх майбутнього відшкодування та отримання прибутку. Критерій ефективності прийняття інвестиційних рішень можна сформулювати таким чином: інвестиційний проект вважається ефективним, якщо його дохідність і ризик збалансовані в прийнятній для учасника проекту пропорції. Формально представимо критерій ефективності у вигляді виразу [25]:
У свою чергу, дохідність інвестиційного проекту як економічну категорію, що характеризує співвідношення доходів та витрат, можна виразити формулою:
Розрахунок показників ефективності та їх характеристику подано в табл. 6.1. Реалізація інвестиційних проектів потребує відмови від коштів сьогодні на користь одержання прибутку в майбутньому. Складність прийняття рішень щодо довгострокових активів полягає в прогнозуванні грошових потоків на значний період часу, Оскільки приплив коштів розподілений у часі, його дисконтування здійснюється за деякою усередненою процентною ставкою δ (ставкою порівняння). Вона має відображати очікуваний усереднений рівень позичкового відсотка на фінансовому ринку [30]. Розрахунок майбутнього фінансового результату за певний період часу називається приведенням майбутнього грошового потоку до результату цього періоду, чи дисконтуванням. Коефіцієнт дисконтування
де α — показник інфляції за розглянутий період часу (як правило, рік), що відбиває знецінювання коштів за цей час. Таблиця 6.1 Критерії обґрунтування рішень під час прийняття
Закінчення табл. 6.1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-28; просмотров: 932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.106.138 (0.011 с.) |

 . (5.4)
. (5.4)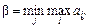 . (5.5)
. (5.5)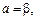 (5.6)
(5.6)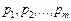 (причому
(причому 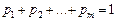 ) застосування стратегій
) застосування стратегій 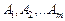 , а гравець В — імовірності
, а гравець В — імовірності 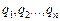 застосування стратегій
застосування стратегій  , де
, де 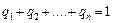 .
.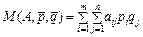 , (5.7)
, (5.7)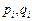 — компоненти цих векторів.
— компоненти цих векторів. . (5.8)
. (5.8)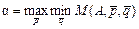 . (5.9)
. (5.9) і
і 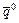 вектори, що відповідають оптимальним мішаним стратегіям гравців А і В, тобто такі вектори
вектори, що відповідають оптимальним мішаним стратегіям гравців А і В, тобто такі вектори  . (5.10)
. (5.10) , тобто
, тобто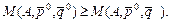 (5.11)
(5.11) ВИСНОВКИ
ВИСНОВКИ ОБҐРУНТУВАННЯ ІНВЕСТИЦІЙНИХ
ОБҐРУНТУВАННЯ ІНВЕСТИЦІЙНИХ  . (6.1)
. (6.1) . (6.2)
. (6.2)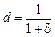 за обраної ставки δ іноді називають бар’єрним коефіцієнтом. В умовах інфляції коефіцієнт дисконтування обчислюється за формулою:
за обраної ставки δ іноді називають бар’єрним коефіцієнтом. В умовах інфляції коефіцієнт дисконтування обчислюється за формулою: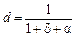 , (6.3)
, (6.3)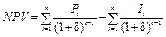 де
де  — грошові надходження за
— грошові надходження за  років завдяки реалізації проекту;
років завдяки реалізації проекту; 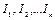 — інвестиції протягом
— інвестиції протягом 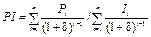
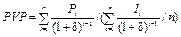
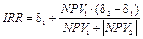 ,
де d1 — ставка дисконту, за якої значення NPV позитивне;
d2 — ставка дисконту, за якої проект стає збитковим, а NPV — від’ємним;
NPV 1 — значення чистої поточної вартості за d1;
NPV 2 — значення чистої поточної вартості за d2
,
де d1 — ставка дисконту, за якої значення NPV позитивне;
d2 — ставка дисконту, за якої проект стає збитковим, а NPV — від’ємним;
NPV 1 — значення чистої поточної вартості за d1;
NPV 2 — значення чистої поточної вартості за d2



