
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок матриці пасажирських кореспонденційСодержание книги
Поиск на нашем сайте ГРАВІТАЦІЙНИМ МЕТОДОМ
Мета заняття – вивчити методику розрахунку матриці пасажирських кореспонденцій гравітаційним методом. Завдання. Визначити матрицю пасажирських кореспонденцій гравітаційним методом. З табл. 4.1 номери транспортних районів обирають за першою цифрою варіанта, а з табл. 4.2 – за другою цифрою. Характеристики транспортних районів наведено у табл. 4.3.
Таблиця 4.1 – Номери транспортних районів
Таблиця 4.2 – Номери транспортних районів
Таблиця 4.3 – Характеристика транспортних районів
Продовження табл. 4.3 Вказівки до виконання завдання 1. Відповідно до заданого варіанта оформити вихідні дані. Наприклад, до варіанта 00 вихідні дані наведені у табл. 4.4.
Таблиця 4.4 – Приклад оформлення вихідних даних
2. Створити координатну модель транспортної мережі. Для цього у двомірній системі координат розмірністю від 0 до 100 в масштабі 1:100000, нарисувати центри транспортних районів і зв’язати їх між собою, щоб центр кожного транспортного району мав не менше трьох і не більше чотирьох зв’язків з іншими центрами. 3. За отриманою координатною моделлю транспортної мережі визначити довжину пересування між районами шляхом вимірювання. Серед існуючих в транспортній мережі зв’язків обрати найкоротші. Результати вимірювань lij занести до таблиці. Приклад представлення матриці найкоротших шляхів наведено у табл. 4.5. 4. Визначити час руху між транспортними районами і трудність сполучення. Час руху розраховують за формулою
де lij – довжина кратчайшого шляху між i-м та j-м районами, км; V – швидкість руху транспортного засобу, км/год. Швидкість руху транспортного засобу приймають 20 км/год. Час на пересування в середині району приймають 2 хв. Трудність сполучення між транспортними районами (dij) визначають з використанням формули:
Результати розрахунків навести в табличному вигляді. Таблиця 4.5 – Матриця найкоротших шляхів
4. Визначити місткість транспортних районів. Селітебну ємкість району (кількість мешканців району, або кількість відправлень) (Нi) розраховують з використанням виразу
де Np – кількість мешканців району, тис. чол.; Нj – трудова ємкість району, тис. чол.; Nм – населення міста, тис. чол.
Трудову ємкість району (кількість прибуття) (Нj) визначають виходячи з припущення, що в розглядуваний період часу (годину “пік”) в райони прибуває 80% всіх працюючих та культурно-побутові пересування у цей час відсутні.
де N – кількість робочих місць у районі, тис. чол. Перевірити умову балансу місткості транспортних районів:
Результати розрахунків подати в табличному вигляді. 5 Визначити матрицю кореспонденцій. 5.1 Матрицю кореспонденцій між транспортними районами розраховати за допомогою гравітаційної моделі (за відправленням).
де кj – коефіцієнт балансування. Розрахунок матриці кореспонденцій – це ітераційний процес. На першій ітерації розрахунку матриці приймають кj=1, а на інших ітераціях коефіцієнт визначають окремо за формулою (4.11). Для спрощення розрахунків введемо позначення
тоді Результати розрахунків подати у табличному вигляді. 5.2 Перевірити умову балансу матриці кореспонденцій. Необхідно оцінити величину відхилення між вихідною величиною трудової ємкості районів (Hj) та трудової ємкості отриманою у результаті розподілу кореспонденцій за гравітаційною моделлю (H’j). Величина відхилення не повинна перевищувати 10%. Відхилення для кожного району розраховують за формулою
Якщо для одного з районів не виконується вимога (4.10), то розраховують за формулою (4.11) коефіцієнт балансування і розрахунок матриці кореспонденцій повторюють вже з новим значенням коефіцієнта на новій ітерації.
6. Зробити висновки за результатами роботи. Висновки за результатами роботи формулюють з урахуванням загальної характеристики гравітаційного методу визначення матриці кореспонденцій та її відхилень, отриманих на різних ітераціях розрахунків. Приклад. Завдання.Розрахувати матрицю пасажирських кореспонденцій гравітаційним методом. Вихідні дані до розрахунку наведені у таблиці 4.6.
Вирішення: 1. Нарисуємо в масштабі 1:100000 координатну модель транспортної мережі. (див. рис. 2). 2. Шляхом вимірювання за координатною моделлю транспортної мережі найдемо найкоротшу довжину пересування між районами lij.. Результати вимірювань представлено у табл. 4.6.
Таблиця 4.6 – Матриця найкоротших шляхів, км.
3. Визначимо з використанням формул (4.1), (4.2) час руху між транспортними районами і трудність сполучення. При розрахунку швидкість руху транспортного засобу приймаємо 20 км/год. Наприклад, час руху між першим та другим районами дорівнює:
Пересування у середині району (t11=t22=…=t10,10=2хв.). Результати розрахунків наведено в табл. 4.7.
Рис. 2 – Графічне відображення транспортної мережі
Таблиця 4.7 – Час руху між транспортними районами, хв.
Наприклад, трудність сполучення для першого транспортного району дорівнює:
Результати розрахунків наведено в табл. 4.8. Таблиця 4.8 – Трудність сполучення між транспортними районами
4. Визначимо місткість транспортних районів. За формулою (4.5) визначимо трудову ємкість районів (кількість прибуття) (Нj):
Результати розрахунків занесені до табл. 4.9.
З використанням формули (4.3) розрахуємо селитебна ємкість районів:
Результати розрахунків занесені до табл. 4.9. Перевіримо умову балансу ємкості транспортних районів: Таблиця 4.9 – Місткість транспортних районів.
5 Розрахунок матриці кореспонденцій. Визначення величини кореспонденцій між i-м та j-м транспортними районами виконуємо із застосуванням гравітаційної моделі (за відправленням). Визначимо елементи матриці Y на першій ітерації. Значення коефіцієнта балансування на першій ітерації кj=1. Наприклад,
Результати розрахунків наведені в табл. 4.10.
Таблиця 4.10 – Значення елементів матриці Y на першій ітерації
Розрахуємо кореспонденції між районами. Наприклад,
Результати розрахунків наведені в табл. 4.11. Перевіримо умови балансу матриці кореспонденцій, використовуючи формулу (4.9). Наприклад,
Результати розрахунків занесено у відповідний рядок табл. 4.11.
Таблиця 4.11 – Матриця кореспонденцій на першій ітерації, тис. чол.
Умова відповідності вихідної величини трудової ємкості районів і трудової ємкості, отримана у результаті розподілу кореспонденцій за гравітаційною моделлю, виконується тільки для третього і шостого транспортних районів. Тому розрахуємо нові значення коефіцієнта балансування і проведемо розрахунок матриці кореспонденцій на новій ітерації. Наприклад,
Значення коефіцієнта для транспортних районів на другій ітерації наведено в табл. 4.12.
Таблиця 4.12 – Значення коефіцієнта балансування на другій ітерації.
Визначимо елементи матриці Y на другій ітерації. Наприклад,
Результати розрахунків наведені в табл. 4.13.
Таблиця 4.13 – Значення елементів матриці Y на другій ітерації.
Розрахуємо кореспонденції між районами. Наприклад,
Результати розрахунків наведені в табл. 4.14.
Таблиця 4.14 – Матриця кореспонденцій на другій ітерації, тис. чол.
Перевіримо умови балансу матриці кореспонденцій. Наприклад,
Результати розрахунків занесені у відповідний рядок табл. 4.14. Розподіл кореспонденцій по транспортних районах на другій ітерації задовольняє умові (4.10), тому на цьому розрахунок матриці кореспонденції завершуємо. 6 Висновок.
Запитання для самоперевірки 1. Обґрунтувати, чим відрізняється кореспонденція міського населення від пасажиропотоку? 2. Що таке рухомість міського населення. Назвати фактори, які впливають на рухомість? 3. Дати назву й охарактеризувати складові етапи принципу, який покладено в основу моделей розрахунку матриці кореспонденцій? 4. Що таке транспортний район, чим він характеризується? За якими принципами формуються транспортні райони міста? Як визначити центр транспортного району для змішаного, житлового та промислового районів? 5. Яка ідея транспортного розрахунку методом взаємних кореспонденцій? 6. Які фактори враховують ймовірні моделі розрахунку взаємних кореспонденцій? Чому гравітаційну модель відносять до ймовірних моделей? 7. Навести математичний вираз і пояснити сенс гравітаційної моделі розрахунку матриці кореспонденцій за відправленням з i-х транспортних районів, за прибуттям в j-ті транспортні райони? У зв’язку з яким фактором гравітаційна модель отримала таку назву? 8. Назвати переваги й недоліки ймовірних моделей розрахунку матриці кореспонденцій? 9. Пояснити поняття “трудова” й “селітебна” ємкість транспортного району? 10. Що таке баланс матриці кореспонденцій, як його виконують? Від чого залежить відхилення від умови балансу матриці кореспонденцій? 11. Яке припущення приймається при визначенні обсягу транспортних районів за прибуттям? 12. Від чого залежить трудність сполучення між транспортними районами? Як її розраховують?
Навчальне видання
Методичні вказівки до виконання практичних робіт з дисципліни “Основи теорії транспортних процесів та систем“ (для студентів 3 курсу денної форми навчання спец. 6.100400 “Транспортні системи“)
Укладач: Андрій Олексійович Шевченко
Відповідальний за випуск В. К. Доля
Редактор М.З. Аляб’єв
План 2005, поз. 125 ____________________________________________________________________ Підп. до друку 11.04.05 Формат 60 84 1/16 Папір офсетний Друк на ризографі. Обл.–вид. арк. 2,5 Тираж 50 прим. Замовл. № Ціна договірна ____________________________________________________________________ 61002, Харків, вул. Революції, 12. Сектор оперативної поліграфії ІОЦ ХНАМГ.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 884; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |

 , (4.1)
, (4.1) . (4.2)
. (4.2)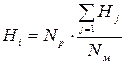 , (4.3)
, (4.3) . (4.4)
. (4.4) , (4.5)
, (4.5) . (4.6)
. (4.6) , (4.7)
, (4.7) , (4.8)
, (4.8)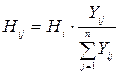 .
. , (4.9)
, (4.9) . (4.10)
. (4.10) . (4.11)
. (4.11)



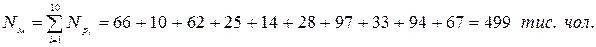
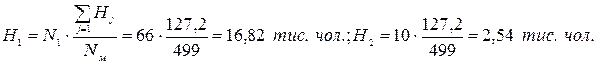
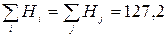 .
.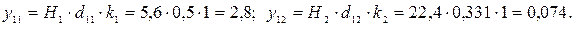





 %
%







