Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вказівки до виконання завданняСодержание книги Поиск на нашем сайте
1. Скласти статистичну лінійну балансову модель міжгалузевих зв’язків (СЛБМ). СЛБМ призначена для визначення змін валового випуску розглядуваного сектора та міжсекторних потоків при різноманітних варіантах зміни потоків сектора кінцевого споживання та валового випуску інших секторів, що входять до складу моделі. Структурними елементами моделі є сектори. Сектор – це різні виробничі комплекси міста (регіону, держави). Кожний виробничий комплекс є виробляючим та споживаючим сектором. Наприклад, сектор „Транспорт” (Т) – це сукупність усіх систем різних видів транспорту, які функціонують у місті; сектор „Паливно-енергетичний комплекс” (ПЕК) – сукупність виробництв, що забезпечують вимоги міста в енергоносіях (вугілля, нафта, газ, електроенергія); „сектор „Виробництво” (В) – галузі економіки, що не включені в інші сектори. Крім виробничих секторів модель включає ще сектор кінцевого споживання. Кінцеве споживання – це споживання, направлене не на виробництво товарів та послуг, а на задоволення вимог людей, які мешкають на території міста. 1.1 Визначити потоки сектора ПЕК, використовуючи значення поставок сектора „Транспорт”. Точність розрахунків у 1-му пункті – один знак після коми:
Поставки сектора „Паливно-енергетичний комплекс” у сектор кінцевого споживання (Y3) зв’язані залежністю
1.2 Розрахувати валовий випуск кожного сектора Xi за наступний період:
де п - кількість секторів у розглянутій моделі; xij – поставки i-го сектора в j-й сектор, млн. грн.; Yi – поставки i-го сектора в сектор кінцевого споживання, млн. грн. 1.3 Подати отримані дані у матричному вигляді, тобто записати СЛБМ:
2. На основі визначеної в попередньому пункті моделі міжгалузевих зв’язків (3.4) розрахувати матрицю коефіцієнтів прямих витрат А. Елементи матриці aij визначають за формулою
де Xj – валовий випуск j-го сектора, млн. грн. Точність розрахунків тут і далі – три знаки після коми. Матриця коефіцієнтів прямих витрат записується у вигляді
3. Розрахувати матрицю коефіцієнтів повних витрат В. Для розрахунку матриці використовуємо матричну формулу:
де Е – одинична матриця.
Вводимо позначення
тоді в лінійному вигляді матрицю D розраховуємо за виразом
Для одержання матриці В необхідно згорнути матрицю D за залежністю
де det D –визначник матриці D; d’ij – алгебраїчне доповнення ij-го елемента матриці D; Т - означає транспоновану матрицю.
Визначник (детермінант) – це число D, утворене з n2 чисел dij елементів, які розташовані в квадратну таблицю з n рядків і n стовбців. Визначник можна розрахувати за правилом «Саррюса» (див. рис. 2). Для визначників другого і третього порядків формули розрахунків такі:
Рис. 2 – Розрахунок визначника за правилом Саррюса
Точність розрахунку визначника - вісім знаків після коми. Розрахувати значення алгебраїчних доповнень. Алгебраїчне доповнення ij -го елемента матриці – це мінор (Мij) елемента, помножений на (-1) у степені (i+j).
Мінор – це визначник під матрицею, який отримають викреслюванням i-го рядка і j-го стовпчика вихідної матриці. Транспонування матриці – це таке перетворення вихідної матриці, в результаті якого рядки вихідної матриці стануть стобцами результуючої матриці. 4. Перевірити правильність обертання матриці В. Після отримання матриці В за (3.9) перевіряємо правильність її обертання, для чого розраховуємо матрицю К:
Для отримання ij-го елемента матриці К при множенні матриць В і D необхідно елементи і-го рядка матриці В помножити на відповідні елементи j-го стовпчика матриці D, а потім скласти розраховані добушки.Сума цих перетворень і дасть шуканий елемент результуючої матриці. Матриця К записуємо у вигляді:
Потім перевіряємо рівність матриць К і Е. Елементи матриць вважаються рівними, якщо різниця між ними існує тільки у третьому знаку після коми:
Матриці рівні між собою, якщо рівні всі їхні елементи, тобто для кожної пари елементів виконується умова (3.16). Якщо 5. Визначити необхідні зміни валового випуску і міжсекторних потоків при зміні векторів кінцевого споживання. Наприклад, поставки сектора «Транспорт» у сектор кінцевого споживання у плановий період збільшуються на 10%, при цьому в інших секторах змін не відбувається. Визначаємо необхідну величину поставок сектора «Транспорт» у сектор кінцевою споживання:
тут і далі апостроф позначає належність елемента до планового періоду. Розраховуємо нове значення валового випуску трьох виробничих секторів за формулою
За матрицею коефіцієнтів прямих витрат А знаходимо нові значення міжсекторних потоків:
Отримані результати рекомендується навести у вигляді матриці СЛБМ:
Валовий випуск секторів і міжсекторних потоків порівнюємо з базовим варіантом матриці, яка розрахована за (3.4) для формулювання висновків. Висновки треба подати у вигляді тексту та порівняльної діаграми. 6. Визначення необхідних змін валового випуску сектора «Транспорт» при зміні векторів кінцевого споживання і валового випуску інших секторів. Визначають величини поставок усіх секторів у сектор кінцевого споживання, а також валовий випуск секторів «Виробництво» і «Паливно-енергетичний комплекс» за формулами
де h1, h2, h3 – коефіцієнти відповідних секторів, що вказують на зміну векторів сектору кінцевого споживання; g2, g3 – коефіцієнти, що вказують на зміну валового випуску секторів «Виробництво» і «Паливно-енергетичний комплекс». На підставі залежностей (3.18) і (3.22) визначають всі можливі моделі для розрахунку валового випуску сектора «Транспорт», за якими розраховують різноманітні його значення:
Для одержання моделей за залежністю (3.22) послідовно змінюється значення індексу i в межах від 1 до 3 і в кожному з варіантів моделі значення валового випуску сектора «Транспорт» виражається через інші змінні. 7. Зробити висновки за результатами роботи. Висновки формулюють на підставі результатів виконання пунктів 5 і 6. У пункті 5 виділяють міжсекторні потоки, які найбільшою мірою змінюються при 10-ти процентному збільшенні обсягу поставок сектора «Транспорт» у сектор кінцевого споживання. Пункт 6 повинен містити зміст про можливість використання моделей для прогнозування обсягу роботи сектора «Транспорт».
Приклад. Завдання.Розрахувати обсяг випуску сектора „ТРАНСПОРТ” у прогнозованому періоді за статичною лінійною моделлю міжгалузевого балансу. Вихідні дані для розрахунків за поточний період наведені в табл. 3.4, 3.5.
Таблиця 3.3 – Значення потоків секторів, млн. грн.
Таблиця 3.4 – Значення коефіцієнтів для розрахунку потоків секторів
Вирішення: 1. Складемо статистичну лінійну балансову модель міжгалузевих зв’язків. 1.1 Використовуючи формули (3.1) і (3.2), визначимо потоки сектора ПЕК.
1.2 Розрахуємо валовий випуск кожного сектора Xi за наступний період за формулою (3.3):
Отримані дані записуємо в матричному вигляді, тобто складаємо СЛБМ:
2. Визначимо валовий випуск секторів із застосуванням СЛБМ. 2.1 На основі визначеної в попередньому пункті моделі міжгалузевих зв’язків і використовуючи формулу (3.5), розрахуємо матрицю коефіцієнтів прямих витрат А:
Матриця коефіцієнтів прямих витрат має вигляд
2.2 Визначимо матрицю коефіцієнтів повних витрат В. Використовуючи формули (3.8), (3.9), розрахуємо матрицю D:
Після розрахунку матриці D проведемо її обертання за формулою (3.10), при цьому необхідно використати формули (3.12), (3.13):
Визначимо алгебраїчне доповнення елементів матриці D. Наприклад, для визначення елемента d’11 викреслюємо перший рядок і перший стовпчик з матриці D, аелементи, що залишилися, утворять шукану субматрицю, яку помножуємо на (-1) у степені (1+1):
Матриця В має наступний вигляд:
2.3 Перевіримо правильність обертання матриці В. Для цього розрахуємо матрицю К. Наприклад, для перших елементів матриці К маємо:
Різниця між елементами матриць К і Е задовольняє вимозі (3.16), тому матриця В розрахована правильно. 3. Визначимо зміни валового випуску і міжсекторних потоків при зміні векторів кінцевого споживання. У перспективному періоді збільшуються на 10% поставки сектора «Транспорт» у сектор кінцевого споживання, при цьому в інших секторах змін не відбуваються:
Розрахуємо нове значення валового випуску трьох виробничих секторів використовуючи формулу (3.18):
З використанням матриці коефіцієнтів прямих витрат А знайдемо нові значення міжсекторних потоків, наприклад:
Отримані результати наведені у вигляді матриці СЛБМ:
Валовий випуск секторів і міжсекторних потоків порівнюють з базовим варіантом матриці, що розрахована за (3.4). Наприклад, x11 =56 млн. грн., x’11 =62,165 млн. грн., тобто власне споживання сектора „Т” збільшилось на 11%; x33= 15335 млн. грн., x’33 =13845,87 млн. грн., тобто власне споживання сектора „ТЕК” зменшилось на 9,71%. Висновки у вигляді тексту та порівняльної діаграми навести в пункті 5. 4. Визначимо зміни валового випуску сектора «Транспорт» при зміні векторів кінцевого споживання і валового випуску секторів «Виробництво» і «Паливно-енергетичний комплекс»:
Використовуючи залежність (3.18) визначимо валовий випуск сектора „Т” на перспективний період при зміні поставок у сектор кінцевого споживання:
На підставі виразу (3.22) визначимо всі можливі моделі для розрахунку валового випуску сектора «Транспорт». Для одержання моделей за залежністю (3.22) послідовно змінюємо значення індексу i у межах від 1 до 3:
Для кожного з варіантів моделі значення валового випуску сектора «Транспорт» зробити висновки щодо можливості використання моделей для прогнозування обсягу роботи сектора та навести їх у пункті 5. 5. Висновки за результатами роботи.
Запитання для самоперевірки
1. Для чого призначена СЛБМ? 2. Дати визначення сектора СЛБМ. Які сектори застосовані в моделі? 3. Обґрунтувати, чому модель міжгалузевих зв’язків називають статистичною? 4. Навести загальну структуру СЛБМ у графічному, табличному й матричному виглядах. 5. Як визначити за моделлю міжгалузевих зв'язків зміни сектора «Т» при зміні поставок у сектор кінцевого споживання та потоків інших секторів. 6. В якій послідовності виконують у моделі прогнозування розвитку транспортної системи? 7. Який сенс має матриця коефіцієнтів прямих витрат при розрахунку потоків? 8. Яким принципом треба керуватися при впорядкуванні матриці міжсекторних потоків. 9. Як виконують обертання матриць та перевірку обертання матриць? 10. Як виконують трансформування матриць? Навести приклади. 11. Що таке мінор матриці? Як його визначити? 12. Що таке алгебраїчне доповнення елемента матриці? Навести приклади. 13. Що таке визначник? Яким чином розраховують визначник другого, третього, четвертого порядків? Навести приклад у загальному вигляді. 14. Виконання, якої умови свідчить про рівність матриць? 15. Як виконують помноження матриць. Навести приклад помноження матриць третього порядку у загальному вигляді?
Заняття 4
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.24.238 (0.009 с.) |

 (3.1)
(3.1) (3.2)
(3.2) , (3.3)
, (3.3) . (3.4)
. (3.4)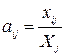 , (3.5)
, (3.5) . (3.6)
. (3.6) , (3.7)
, (3.7) ,
,  .
. , (3.8)
, (3.8) , (3.9)
, (3.9) , (3.10)
, (3.10) (3.11)
(3.11) . (3.12)
. (3.12)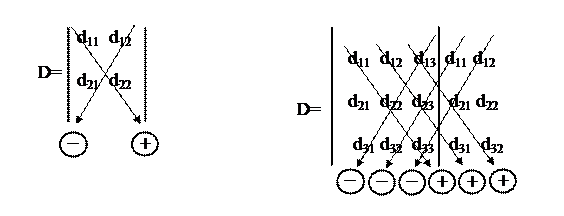
 . (3.13)
. (3.13) . (3.14)
. (3.14) (3.15)
(3.15) . (3.16)
. (3.16) , перевіряється правильність розрахунку матриці В.
, перевіряється правильність розрахунку матриці В. (3.17)
(3.17) . (3.18)
. (3.18) . (3.19)
. (3.19) . (3.20)
. (3.20) (3.21)
(3.21) (3.22)
(3.22)

 .
.
 .
. .
.
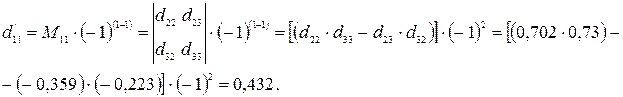



 .
.


 .
.