
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найпоширенішими методами розробки господарських рішень є аналітичні, статистичні методи, методи математичного програмування, евристичні, експертні методи, метод сценаріїв, метод «дерева рішень».Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обґрунтування ГР — підкріплення переконливими доказами відповідності передбачуваного рішення заданим критеріям та реальним обмеженням. Процедура вибору методів для обґрунтування конкретних ГР має охоплювати: аналіз господарської задачі щодо її змісту, можливості формалізації; вибір методів для пошуку оптимального варіанту рішення; визначення правил і умов застосування обраних методів. Методи обґрунтування рішення, як правило, використовуються комплексно, що зумовлено наявністю формальних і неформальних факторів, які створюють ситуацію. Можливо виокремити три підходи до обґрунтування та вибору рішень: концепція математичного вибору рішень (нормативний підхід); якісно-предметна концепція (дескриптивний підхід); комплексна концепція рішень. Мета прогнозування — зробити зрозумілим процес розробки рішення; допомогти виявити базові тенденції в досліджуваній сфері; визначити основні критичні зони, врахувати ризики стрибкоподібних змін; запропонувати варіанти стратегій досягнення мети управління. Основні задачі прогнозування: визначення проходження процесу зміни об’єкта прогнозування протягом майбутнього періоду; обґрунтування економічної доцільності розробки ГР, виходячи з наявних ресурсів та пріоритетів.
НЕВИЗНАЧЕНІСТЬ Сутність та види невизначеності У процесі функціонування суб’єкти підприємництва зазнають впливу ряду чинників — соціально-політичних, адміністративно-законодавчих, виробничих, комерційних, фінансових тощо. Майбутній розвиток ситуацій, кінцеві результати господарських операцій спрогнозувати дуже складно, оскільки прийняття рішень в економіці на всіх рівнях управління відбувається в умовах неоднозначності розвитку, неможливості точного прогнозування певних подій, неповної чи недостовірної інформації. Усунути невизначеність майбутнього в підприємницькій діяльності неможливо, тому що вона являє собою елемент об’єктивної дійсності. Умови невизначеності є предметом досліджень й об’єктом постійного спостереження з боку економістів та спеціалістів інших сфер. Одним із перших учених, який займався вивченням проблеми невизначеності в рамках сучасної економічної теорії, був Френк Найт. З погляду економічної теорії невизначеність — це об’єктивна неможливість здобуття абсолютного знання про об’єктивні та суб’єктивні фактори функціонування системи, неоднозначність її параметрів. Чим більша невизначеність під час прийняття господарського рішення, тим більший ступінь ризику. Кількісно невизначеність може виступати як можливість відхилення результату від очікуваного (або середнього) значення як у менший, так і в більший («спекулятивна» невизначеність) бік, або можливість тільки негативних відхилень кінцевого результату події («чиста» невизначеність) [30]. Основні причини невизначеності схематично подано на рис. 4.1.
Рис. 4.1. Основні причини невизначеності Економіка ринкового типу передбачає існування найрізноманітніших видів невизначеності для всіх суб’єктів господарювання (рис. 4.2). Найпоширенішою є класифікація невизначеності за ступенем настання події. Ця класифікація дає можливість розрізнити повну та часткову невизначеність, повну визначеність. Часткова чи повна невизначеність пояснюється тим, що, по суті, економічні проблеми зводяться до задач вибору з деякої кількості альтернатив. При цьому економічні суб’єкти не мають повної інформації про стан систем для розробки оптимального рішення й достатніх можливостей для адекватного обліку всіх доступних даних. Невизначеність інформації можливо зняти, визначивши ймовірність, з якою можна очікувати цю інформацію. Залежно від засобів визначення ймовірності розрізняють два типи невизначеності — статистичну та нестатистичну. Якщо мається на увазі статистична невизначеність, то іноді кажуть, що рішення приймається в умовах ризику, якщо нестатистична — то рішення приймається в умовах невизначеності. У чистому вигляді той чи інший вид імовірності трапляється рідко — найчастіше можна зустріти мішаний вид.
Рис. 4.2. Схема видової класифікації невизначеності Розвиток фірми в умовах ринкової економіки на кожному етапі повинен формуватися з врахуванням різних видів невизначеності. Чинники невизначеності, що впливають на будь-який ринковий суб’єкт, також наявні безпосередньо в процесі управління ним. За місцем виникнення невизначеність в управлінні підприємством (фірмою) може бути наслідком: · невизначеності у встановленні планового періоду і, зокрема, періоду, на який розробляється стратегія розвитку підприємства; · невизначеності формування цілей підприємства та вибору пріоритетів у визначених цілях, що може бути зумовлено наявністю ряду альтернативних цілей; · помилок в оцінках дійсного стану справ усередині самого підприємства та його місця на ринку, до чого, у свою чергу, може призвести ряд причин об’єктивного та суб’єктивного характеру; · неповної або помилкової інформації стосовно перспектив розвитку даного підприємства й ринку в цілому, рішень, прийнятих на її підставі; · можливих перебоїв у розробці чи реалізації стратегії розвитку підприємства; невизначеності контролю й оцінки результатів діяльності підприємства. Таким чином, невизначеність виступає невід’ємним атрибутом прийняття господарських рішень. Але слід зазначити, що вона не завжди є негативним фактором, оскільки усвідомлення факту її існування мотивує до самостійного розв’язання господар- На практиці зниження рівня невизначеності, необхідне для прийняття господарських рішень, забезпечується: Ø збором інформації, що зменшує невизначеність очікувань; Ø обробкою інформації методами аналізу, прогнозу, сценарію та з’ясуванням причин, форм і наслідків невизначеності; Ø розробкою моделей, адекватних ситуаціям, що мають місце, і здобуттям у результаті моделювання значень цільових величин, функціональних залежностей станів об’єкта управління та навколишнього середовища. 4.2. Критерії прийняття рішень Багато рішень у підприємницькій діяльності доводиться приймати в умовах, коли необхідно вибирати напрями дій з кількох можливих варіантів, результати здійснення яких важко спрогнозувати. Невизначеність виступає основною характеристикою недостатньої забезпеченості процесу прийняття економічних рішень знаннями щодо певної проблемної ситуації. На теоретичному рівні ця ситуація досить добре розроблена, проте на практиці застосування формалізованих алгоритмів аналізу обмежене. Основні труднощі полягають у тому, що неможливо оцінити ймовірність появи наслідків прийнятих рішень. Для вибору оптимальної стратегії в ситуації невизначеності використовують кілька критеріїв. Кожен з критеріїв передбачає як оптимальне рішення використовувати тільки одну конкретну стратегію («чисту» стратегію). Але в деяких випадках краще не дотримуватися одної стратегії, а застосовувати декілька («мішану» стратегію). За наявності кількох альтернативних станів зовнішнього середовища і внутрішніх умов підприємства, їм відповідають належні значення цільових функцій. Якщо жодна з альтернатив не домінуватиме, то постає задача вибору рішення із застосуванням правил і критеріїв теорії прийняття рішень. Наведемо кілька загальних критеріїв раціонального вибору варіантів рішень з безлічі можливих. Критерії засновані на аналізі матриці можливих станів навколишнього середовища й альтернатив рішень. Для прийняття рішень в умовах невизначеності та ризику за допомогою статичної ігрової моделі вхідна інформація подається у вигляді матриці, рядки якої — це можливі альтернативні рішення, а стовпчики — стани системи (середовища). Кожній альтернативі рішень і кожному стану системи (середовища) відповідає результат (наслідок рішення), який визначає витрати або виграш за вибору даної альтернативи рішення та реалізації даного стану системи. У дискретному випадку дані задаються у формі матриці, представленої в табл. 4.1. Таблиця 4.1 Матриця прибутків
Аі — альтернатива і -го рішення (і = n); Sj — можливий j -стан навколишнього середовища (j = 1, m); aij — результат (наслідок рішення). У загальному вигляді aij — неперервна функція аргументів Аі та Si, що позначає вартість капіталу, прийняту альтернативою j за стану навколишнього середовища і. Матриця придатна для ситуації, коли: · існує кінцева кількість розглянутих альтернатив дій і станів навколишнього середовища; · має місце функція результатів, яка зараховує кожній альтернативі однозначний ефект у формі, наприклад, вартості капіталу, доходів, прибутків тощо; · вартість капіталу чи отриманий прибуток (зазнаний збиток) буде єдино важливою цільовою величиною. Альтернативи в зазначених умовах можуть вибиратися за одним із критеріїв, поданих у табл. 4.2, відповідно до правил прийняття рішень. Нехай кожна альтернатива має однозначний ефект у формі вартості капіталу. Для вибору оптимальної стратегії в ситуації невизначеності використовуються різні правила та критерії (див. табл. 4.2). Таблиця 4.2 Характеристика критеріїв обґрунтування
Закінчення табл. 4.2
Приклад розрахунку критеріїв для прийняття рішень в умовах невизначеності подано в розділі 5. 4.3. Теорія корисності в системі Проблема раціонального вибору є однією з головних економічних задач. Її постійно розв’язують основні суб’єкти економіки — виробники та споживачі. Виробники намагаються найвигідніше вкласти капітал у виробництво товарів, які приносять дохід. Споживачі бажають придбати продукцію з високою споживчою цінністю та за прийнятною ціною. Кожна з цих задач розв’язується в умовах ризику. Результати рішень залежать від випадкових величин, які характеризуються ймовірнісними функціями розподілу. Для того, щоб порівнювати їх ефективність, необхідно вміти порівнювати функції розподілу ефективності. Для задач прийняття рішень в умовах ризику та невизначеності принцип оптимального вибору часто описується за допомогою функції корисності. Корисність виражає ступінь задоволення особи від споживання товару чи виконання будь-якої дії. В економічному аналізі корисність часто застосовується для того, щоб описати пріоритет у ранжуванні наборів споживчих товарів і послуг. Основним припущенням економічної теорії є припущення про те, що людина завжди робить раціональний вибір. Поняття функції корисності дає можливість зіставити споживчий ефект від купівлі (продажу) різних, навіть фізично несумісних, товарів (ефект від купівлі однієї сорочки й однієї книги). Корисність розглядається як певним чином узагальнені втрати чи виграші, коли всі цінності зведено до однієї шкали. Корисність вимірюють у довільних одиницях, що називаються одиницями корисності, які можна пов’язати з іншими одиницями, наприклад, грошовими. Цей зв’язок і визначає величину корисності для особи, що приймає рішення. Людина завжди обирає той варіант, корисність якого, на її думку, максимальна. Функцією корисності називається деяка функція Аксіоми раціональної поведінки наведено у праці Дж. Фон Неймана та О. Моргенштерна. За умови виконання цих аксіом автори довели теорему про існування деякої функції, що регулює раціональний вибір, — функції корисності [31]. Аксіома 1 (повноти). Коли підприємець стикається з двома будь-якими рядами подій, він завжди може сказати, який йому більше до вподоби або йому байдуже, який із рядів подій вибрати. Ця аксіома записується у вигляді: — X ≥ Y (X більше до вподоби, ніж Y, або байдуже); — X ≈ Y (X і Y рівноцінні); — X > Y (X більше до вподоби, ніж Y). Завдяки аксіомі повноти споживач наділяється здатністю класифікувати (розрізняти) ряди подій, тобто вмінням порівнювати всі альтернативи. Аксіома 2 (транзитивності). Перевага серед різних рядів подій послідовна, тобто, якщо ряд X > Y, Y > Z, то X > Z. Завдяки аксіомі транзитивності виключається мінливість смаків споживача. Припустимо, що споживач віддає перевагу ряду подій f над рядом d, а ряду d над рядом b, ряду b над рядом подій f. Отже, щоб господарювання було раціональне, підприємець повинен мати усталений смак, інакше він ніколи не зможе зробити правильний вибір. Аксіома 3 (неперервності). В умовах аксіоми транзитивності відносно альтернатив X, Y, Z припустимо, що з імовірністю 1 індивід може отримати Y, з імовірністю p — X, а з ймовірністю Аксіома 4 (незалежності). Нехай існують блага або товари X і Y, які, на думку індивіда, однакові, та дві лотереї, які відрізняються лише тим, що одна містить X, а друга — Y, тоді ці дві лотереї для індивіда однакові. Аксіома 5 (нерівних імовірностей). Якщо індивіду запропонувати дві лотереї, які дають однаковий виграш із різною ймовірністю, то він обирає ту, ймовірність виграшу якої більша. Аксіома 6 (складеної лотереї). Коли призом однієї лотереї є білет іншої лотереї, то індивід приймає рішення лише з міркувань імовірностей виграшу кінцевого призу. Для визначення корисності використовують поняття лотереї [8]. Для цього експерту пропонують порівняти дві альтернативи: 1) значення показника X; 2) лотерею: отримати Величину ймовірності Для того щоб оцінити проміжний результат, особі пропонують взяти участь у лотереї. Значення Корисність варіанту 1) отримати гарантовано 100 грн; 2) узяти участь у лотереї: або одержати 50 грн з імовірністю 0,4, або отримати 150 грн із відповідною ймовірністю 0,6. Для кожної людини буде своє значення ймовірності, за якої їй байдуже, що обирати: гроші гарантовано або участь у лотереї. Імовірність перетворюють на корисність, помножуючи на 100, якщо корисність визначається за 100-бальною шкалою, або помножуючи на 10, коли за 10-бальною. Нехай лотерея Математичне сподівання виграшу, тобто очікуваний виграш, обчислюють за формулою:
Математичне сподівання корисності, тобто очікувану корисність, визначають за формулою:
Корисність результатів збігається з математичним сподіванням корисності результатів. Взаємозв’язок ризику з функціями корисності визначається поняттям детермінованого еквіваленту. Детермінований еквівалент лотереї — це гарантована сума
Особу, що приймає рішення, називають несхильною до ризику, коли для неї найбільш пріоритетною є можливість одержати гарантовано очікуваний виграш у лотереї, ніж узяти в ній участь. Із теорії корисності можна зробити висновок, що корисність лотереї збігається з математичним сподіванням корисності її випадкових результатів. Відповідно до цього умова несхильності до ризику набуває такого вигляду:
тобто корисність сподіваного доходу більше сподіваної корисності. ОПР не схильна до ризику тоді й тільки тоді, коли її функція корисності увігнута. Для функції корисності можна розрахувати премію за ризик у лотереї (p(х)) як різницю між очікуваним виграшем і детермінованим еквівалентом:
За своїм фізичним змістом премія за ризик (надбавка за ризик) — це сума в одиницях виміру показника X, якою суб’єкт управління згоден поступитися із середнього виграшу, щоб уникнути ризику, пов’язаного з лотереєю, і отримати гарантований дохід без ризику. Коли особа, що приймає рішення, натрапляє на лотерею, менш пріоритетну, ніж стан, у якому вона в даний момент перебуває, то постає питання, скільки б вона заплатила (в одиницях вимірювання критерію X) за свою неучасть у цій лотереї (уникнення її). Страхова сума (CC) — це величина детермінованого екві-
Умова схильності до ризику набуває такого вигляду:
тобто корисність сподіваного доходу менше сподіваної корисності. ОПР схильна до ризику тоді й тільки тоді, коли її функція корисності опукла, а графік розгорнутий дзвоном униз. Премія за ризик у випадку схильності до ризику показує, скільки коштів інвестор може додатково отримати або втратити, ризикуючи. Умова байдужості до ризику набуває такого вигляду:
ОПР байдужа до ризику тоді й тільки тоді, коли її функція корисності лінійна, а графік — пряма.Премія за ризик у випадку байдужості до ризику завжди дорівнює нулю. Розглянемо приклади функцій корисності:
1. Зростаюча функція корисності для суб’єкта управління, байдужого до ризику: U (х) = а + bх. 2. Зростаюча функція корисності для суб’єкта управління, несхильного до ризику: U (х) = log(x + b), де х > – b. 3. Зростаюча функція корисності для суб’єкта управління, схильного до ризику: U (х) = х 2, де
У теорії ринку цінних паперів широко використовується квадратична функція корисності вигляду:
де А — задане число. Зміст цієї функції такий: інвестор вважає корисним для себе збільшити значення ефективності, але бажає уникнути відхилення цієї ефективності від сподіваного значення. Чим більше А, тим більше тенденція запобігання ризику, тобто А — міра несхильності до ризику, а 1/ А — міра схильності до ризику. За допомогою функції корисності можна розраховувати ймовірність банкрутства:
або 0, якщо де K — початковий капітал. Методика побудови функції корисності для будь-якого економічного показника складається з таких кроків: Крок 1. Виявити найкращі та найгірші з можливих допустимих показників і присвоїти їм значення корисності відповідно 100 і 0 (якщо корисність оцінюється за 100-бальною шкалою). Крок 2. Розглянути кілька проміжних показників і вказати їхнє значення корисності (кожним експертом окремо). Крок 3. Розрахувати середні оцінки корисності проміжних значень, вказаних експертами. Крок 4. Якщо спостерігається розсіювання значень якогось із показників, то потрібно повернутися до кроку 2, аби узгодити думки експертів для досягнення прийнятного діапазону розсіювання оцінок (кроки 2—4 можуть повторюватися кілька разів). Крок 5. Визначення функції корисності через побудову функції регресії методом найменших квадратів (простіша функція корисності — рівняння прямої). Вид і аналітична форма функції корисності свідчить про відношення суб’єкта, що приймає рішення, до ризику.
Визначення корисності за допомогою математичних функцій. Умови задачі Фірма має прийняти рішення на основі трьох показників ефективності, застосовуючи різне відношення до ризику: несхильність, схильність, нейтральність. Показники ефективності задано лотереями: L 1 = (20; 0,4; 10), L 2 = (5; 0,5; 6), L 3 = (10; 0,7; 30). Несхильність до ризику задана функцією корисності: U (x) = Схильність задано функцією корисності: U (x)= 0,4 х. Нейтральність задано функцією корисності: U (x) = 4 + 1,2 х. Необхідно: розрахувати премію за ризик (надбавку) та визначити, яким відношенням до ризику має скористатися фірма. Розв’язання 1. Визначимо сподіваний виграш
Сподіваний виграш показує, яку середню ефективність може мати фірма від рішення не брати участі в лотереї. 2. Визначимо очікувану корисність показника ефективності за різних відношень до ризику (е = 2,71). М 1 = (1 – 2 е – 0,1 · 20) · 0,4 + (1 – 2 е – 0,1 · 10) · 0,6 = 0,4 – 0,8 / 2,712 – М 2 = (0,4 · 202) · 0,4 + (0,4 · 102) · 0,6 = 64 + 24 = 88; М 3 = (0,4 + 1,2 · 20) · 0,4 + (4 + 1,2 · 10) · 0,6 = 11,2 + 9,6 = 20,8. 3. Визначимо детермінований еквівалент — гарантовану суму а) несхильність до ризику: б) схильність до ризику: в) нейтральність:
Премія за ризик у випадках несхильності до ризику показує, які кошти може втратити інвестор, не ризикуючи: (0,25 / 14) × Премія за ризик у випадку схильності до ризику показує, яку величину коштів інвестор може додатково отримати або втратити, ризикуючи: (0,85 / 14) · 100 % = 6,07 %. Премія за ризик у випадку нейтральності завжди 0. Висновок: У даній ситуації краще ризикувати.
Визначення корисності господарських рішень графічним методом. Умови завдання Підприємство має тимчасово вільні кошти — 10 000 грн і вирішує питання про їх використання за двома варіантами. По-перше, можна вкласти гроші в деякий інвестиційний проект. У випадку невдачі підприємство втрачає свої гроші, а у випадку успіху — через рік отримує 40 000 грн. По-друге, альтернативний варіант — вкласти гроші в банк під 9 % річних без ризику. У випадку вкладання коштів у інвестиційний проект спеціаліст з маркетингу вважає, що ймовірність успіху — 0,3. Щоби прийняти рішення стосовно використання підприєм- Таблиця 1 Корисність різних сум доходів на думку директора
Потрібно: визначити варіант вкладання коштів за допомогою критерію сподіваного доходу; побудувати два графіки корисності та визначити за ними відношення до ризику обох спеціалістів; визначити корисність доходів за умовами директора і бухгалтера та вказати, що порадить кожен із них за правилом сподіваної корисності. Розв’язання Спочатку розрахуємо сподівані доходи для обох варіантів вкладання коштів (табл. 2). Таблиця 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-28; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.43 (0.015 с.) |

 Частина
Частина
 РИЗИК ТА НЕВИЗНАЧЕНІСТЬ
РИЗИК ТА НЕВИЗНАЧЕНІСТЬ 

 , визначена на множині переваг, якщо вона монотонна, тобто з того, що
, визначена на множині переваг, якщо вона монотонна, тобто з того, що  , випливає
, випливає  . Цінні папери та майбутні інвестиції також є товаром, тому, з одного боку, їх ефективності можна розрахувати, бо вони мають грошову оцінку. Але ризикові цінні папери або інвестиції гарантують отримання грошей у майбутньому, і тут зіставити їх ефективність неможливо. Встановлення будь-якого ступеня ризику, характеризуючи випадкову величину одним числом, є спробою подолати цю суперечність.
. Цінні папери та майбутні інвестиції також є товаром, тому, з одного боку, їх ефективності можна розрахувати, бо вони мають грошову оцінку. Але ризикові цінні папери або інвестиції гарантують отримання грошей у майбутньому, і тут зіставити їх ефективність неможливо. Встановлення будь-якого ступеня ризику, характеризуючи випадкову величину одним числом, є спробою подолати цю суперечність. з імовірністю
з імовірністю  або
або  з ймовірністю
з ймовірністю  —
—  .
. змінюють поступово до такої величини від 0 до 1, доки, на думку експерта, значення показника
змінюють поступово до такої величини від 0 до 1, доки, на думку експерта, значення показника  і лотерея
і лотерея  стануть еквівалентними. Тобто всі можливі результати розміщують за зростанням. Корисність найгіршого результату оцінюється як 0, а найкращого — 1 (або як 100):
стануть еквівалентними. Тобто всі можливі результати розміщують за зростанням. Корисність найгіршого результату оцінюється як 0, а найкращого — 1 (або як 100):  .
. за якого особа відмовиться від гарантованого результату на користь участі у лотереї, беруть для розрахунку корисності:
за якого особа відмовиться від гарантованого результату на користь участі у лотереї, беруть для розрахунку корисності:  . Тобто із множини значень відомого показника
. Тобто із множини значень відомого показника  , де
, де  приводить до виграшів (подій)
приводить до виграшів (подій)  із відповідними ймовірностями
із відповідними ймовірностями  і відповідними корисностями
і відповідними корисностями  .
. . (4.1)
. (4.1) . (4.2)
. (4.2) отримання якої екві-
отримання якої екві- . (4.3)
. (4.3) , (4.4)
, (4.4) . (4.5)
. (4.5) . (4.6)
. (4.6) , (4.7)
, (4.7) . (4.8)
. (4.8) х > = 0.
х > = 0. , (4.9)
, (4.9) , якщо
, якщо  ,
, ,
,
 , отримання якої еквівалентно участі в лотереї. Це середнє значення показника ефективності за відповідного відношення до ризику:
, отримання якої еквівалентно участі в лотереї. Це середнє значення показника ефективності за відповідного відношення до ризику: . З цього
. З цього 

 , звідси
, звідси  ;
; , звідси
, звідси  . Завжди має дорівнювати
. Завжди має дорівнювати  .
. ,
,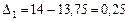 ;
;  ;
;  .
.


