
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вибір оптимального рішення за критерієм БайєсаСодержание книги
Поиск на нашем сайте
За критерієм Байєса оптимальним буде альтернативне рішення А 3. Критерій Лапласа характеризується невідомим розподілом імовірностей на множині станів середовища та базується на принципі «недостатнього обґрунтування», який означає: коли немає даних для того, щоби вважати один зі станів середовища більш імовірним, то ймовірності станів середовища треба вважати рівними. Оптимальну альтернативу за критерієм Лапласа знаходимо за формулами: для для Таблиця 3 Вибір оптимального рішення за критерієм Лапласа
За критерієм Лапласа оптимальним буде альтернативне рішення А 3 (табл. 3). За правилом максимакс альтернативу знаходимо за формулою:
Скориставшись цим правилом, визначаємо максимальні значення для кожного рядка та вибираємо найбільше з них. За правилом максимакс оптимальним буде альтернативне рішення А 3 (табл. 4). Таблиця 4 Вибір оптимального рішення за правилом максИмакс
Критерій Вальда вважається найобережнішим із критеріїв. Оптимальне альтернативне рішення за цим критерієм знаходимо за формулами: для для Таблиця 5 ВИБІР ОПТИМАЛЬНОГО РІШЕННЯ ЗА КРИТЕРІЄМ ВАЛЬДА
За критерієм Вальда оптимальними будуть альтернативні рішення А1 і А3, які вважаються еквівалентними, тобто мають однакові переваги для виконання. Для того щоб застосувати критерій Севіджа, потрібно побудувати матрицю ризику як лінійне перетворення функціоналу оцінювання.
Для побудови матриці ризику використаємо такі формули: для для Матрицю ризику побудуємо в табл. 6. Таблиця 6 Побудова матриці ризику
Тепер можна застосувати критерій Севіджа до матриці ризику за формулою:
Таблиця 7 Вибір оптимального рішення за критерієм Севіджа
За критерієм Севіджа оптимальним буде альтернативне рішення А 3 (табл. 7). За допомогою критерію Гурвіца встановимо баланс між випадками крайнього оптимізму ат випадками крайнього песимізму за допомогою коефіцієнта оптимізму a. Цей коефіцієнт визначається від нуля до одиниці та показує ступінь схильностей особи, що приймає рішення, до оптимізму чи песимізму. Якщо a = 1, то це свідчить про крайній оптимізм, якщо a = 0 — крайній песимізм. За умов задачі a = 0,6. Оптимальну альтернативу за критерієм Гурвіца знаходимо за формулами: для для Оптимальним рішенням за критерієм Гурвіца буде альтернативне рішення А 3 (табл. 8). Таблиця 8 Вибір оптимального рішення за критерієм Гурвіца
Висновок: розрахунок за всіма даними критеріями довів доцільність виробництва продукції за альтернативним варіантом А 3. 5.3.2. Прийняття господарських рішень Ситуація конфлікту є невід’ємною складовою ринкового середовища, під час якої кожен із суб’єктів (конкурентів) намагається завдати збиток іншому та мінімізувати власні витрати. Конфліктною називається ситуація, коли стикаються інтереси двох чи більше сторін, які мають суперечливі цілі, причому виграш кожної зі сторін залежить від того, як поводитимуться інші [31; 58]. Приклади конфліктних ситуацій: «бойові» дії, біржові угоди, різні види виробництва в умовах конкуренції, угоди на фондовому ринку, спортивні змагання, змагання, ігри. У житті конфлікт за-
Рішення в умовах конфлікту завжди пов’язані з ризиком, тому необхідним є обґрунтований підхід у виборі напряму подальших дій. Підприємець у процесі своїх дій повинен вибрати таку стратегію, що дасть змогу йому зменшити ступінь протидії, що, у свою чергу, знизить ступінь ризику. Математичний апарат для вибору відповідного господарського рішення в конфліктній ситуації сформований у теорії ігор. Завдяки їй: ü підприємець або менеджер краще розуміють конкретну обстановку, проблему в цілому та зводять до мінімуму ступінь ризику; ü можна вирішувати багато економічних проблем, пов’язаних з вибором, визначенням найкращого стану, підпорядкованого тільки деяким обмеженням, що випливають з умов самої проблеми; ü підприємець (менеджер) спонукується розглядати всі можливі альтернативи як своїх дій, так і стратегії партнерів, конку- Мета теорії ігор — формування рекомендацій щодо оптимальної поведінки учасників конфлікту, тобто визначення оптимальної стратегії кожному з них. У теорії ігор розроблено систему власних понять [31]. Математична модель конфлікту називається грою, сторони у конфлікті — гравцями. Результат гри називається виграшем, програшем або нічиєю, правила гри — перелік прав і обов’язків гравців. Ходом називається вибір гравцем однієї з передбачених правилами гри дій. Ходи бувають особисті та випадкові. Особистий хід — це свідомий вибір гравця, випадковий хід — вибір дії, що не залежить від його волі. Залежно від кількості можливих ходів у грі ігри поділяються на скінченні та нескінченні. Скінченні — ті, котрі передбачають нескінченну кількість ходів, нескінченні — навпаки. Деякі ігри в принципі мають вважатися скінченними, але мають так багато ходів, що належать до нескінченних (шахи). Стратегією гравця називається сукупність правил, що визначають вибір варіанту дій у кожному особистому ході. Оптимальною стратегією гравця називається така, що забезпечує йому максимальний виграш. Ігри, що складаються тільки з випадкових ходів, називаються азартними. Ними теорія ігор не займається. Її ме- Основне припущення, на підставі якого знаходять оптимальне рішення в теорії ігор, полягає в тому, що супротивник такий же розумний, як і сам гравець. У грі грають два гравці, назвемо їх А і B. Себе прийнято ототожнювати з гравцем А. Нехай в А є m можливих стратегій:
Гра може мати нормальну (матричну) форму або розгорнуту (у вигляді дерева). Гру зручно відображати таблицею, що називається платіжною матрицею, або матрицею виграшів (табл. 5.2). Платіжна матриця має стільки стовпців, скільки стратегій у гравця B, і стільки рядків, скільки стратегій у гравця A. На перетині рядків і стовпців, що відповідають різним стратегіям, стоять виграші гравця A і, відповідно, програші гравця B. Зведення гри до матричної форми саме по собі може бути важким і навіть нездійсненним завданням унаслідок незнання стратегій, величезної їх кількість, а також через складність оцінювання виграшу. Ці приклади і мають на меті показати обмеженість даної теорії, тому що в усіх подібних випадках задача не може бути розв’язана методами теорії ігор. Таблиця 5.2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-28; просмотров: 451; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.50.186 (0.012 с.) |


 ; (3)
; (3)
 . (4)
. (4)
 . (5)
. (5) ; (6)
; (6) . (7)
. (7) (8)
(8) (9)
(9) . (10)
. (10) . (5.11)
. (5.11)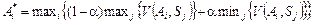 . (5.12)
. (5.12)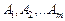 , а в супротивника B — n можливих стратегій:
, а в супротивника B — n можливих стратегій:  . Така гра називається грою
. Така гра називається грою  . Позначимо через
. Позначимо через 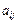 виграш гравця A за власної стратегії
виграш гравця A за власної стратегії  і стратегії супротивника
і стратегії супротивника  . Зрозуміло, що можлива кількість таких ситуацій —
. Зрозуміло, що можлива кількість таких ситуацій — 


