
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Види просторового розподілу. Розподіл полігонів та розподіл ліній.Содержание книги
Поиск на нашем сайте
Для правильної оцінки оточення потрібно знати також відношення між окремими елементами, які ми бачимо, та простором між ними. Тепер ми будемо розглядати не обсяг простору, який займає об’єкт, або його форму, а розміщення об’єктів у просторі, яке ми можемо характеризувати кількістю об’єктів у визначеній області, і як вони розподілені – рівномірно або групами. Існуюча різниця в просторовому розміщенні об’єктів, дозволяє нам сформулювати питання, що це за розподіл, як ці об’єкти можливо класифікувати, яку інформацію вони несуть про процеси, що призвели до їх створення. Спочатку необхідно встановити, що ми розуміємо під просторовим розподілом. Просторовий розподіл – це розставлення, упорядкування, концентрація або розосередження, з’єднання або відсутність зв’язку об’єктів в межах географічного простору, що їх містить. В якості об’єктів на карті виступають точки, лінії та площинні об’єкти (полігони). Тому і методи аналізу просторового розподілу застосовуються до кожної групи об’єктів, в залежності від їх типу, окремо. Розглянемо їх сутність більш докладно. Розподіл точок. Точковими об’єктами можуть бути різні об’єкти місцевості (криниці, дерева, будинки, тощо і навіть міста, в залежності від масштабу). Крім того, точкові об’єкти можуть подаватися у вигляді ліній і областей. Найпростішою мірою точкового розподілу є щільність точок. Вона визначається як результат ділення кількості точок на загальну площу, на якій вони розміщені. Щільність населення, забудови, дерев тощо – широко використовується як міра компактності точок. Порівнявши значення щільності подібних об’єктів в різних областях, ми можемо порівняти механізми, що діють в цих областях. Крім того, можливість порівняння точки в одному теж самому місті, але в різні моменти часу, дозволить нам побачити зміну щільності у часі. Крім загальної щільності розподілу, нас може цікавити ще і його форма. Точкові об’єкти зустрічаються в одному з чотирьох можливих варіантів характеристик. Рівномірний розподіл – коли кількість точок на одиницю площі в кожній малій підобласті така, як і в будь-якій іншій підобласті. Якщо точки розміщені у вузлах сітки, з однаковими інтервалами по всій області, то рівномірний розподіл називається регулярним. В інших випадках, рівномірно розподілені точки розміщуються у випадковому порядку по всій області, що розглядається. Зустрічаються випадки, коли точки зібрані у компактні групи, і такий розподіл називається згрупованим або кластерним.
Аналіз квадратів. Рівномірні точкові розподіли визначаються на основі відношень між однаковими підобластями, які називають квадратами. Це дуже поширений метод аналізу дискретних даних. Точками тут можуть бути будь-які окремі об’єкти. Якщо кожний квадрат містить приблизно однакову кількість точок, то розподіл є рівномірним. В стандартному методі аналізу квадратів (для рівномірного розподілу) мипередбачаємо, що приблизно одна і та ж кількість об’єктів буде знаходитися у кожній підобласті, що дорівнює загальній кількості об’єктів, що поділені на кількість підобластей. Для перевірки рівномірності розподілу використовується статистичний показник, що називається критерій c2 (хи-квадрат). Він обчислюється за формулою: c2 = де: Q – кількість точок в квадраті; Е – очікувана кількість точок в квадраті. Складання результатів підрахунків здійснюється за всіма квадратами. Якщо отримане число незначно відрізняється від того, що очікується, то розподіл є рівномірним. Коли ж число значно відрізняється від того, що повинно бути, то цей фактор говорить про деяку нерівномірність у розподілі точкових об’єктів. На практиці такий аналіз виконується за допомогою спеціалізованої програми, яка входить до складу програмного забезпечення геоінформаційної системи. Аналіз найближчого сусіда. Крім аналізу точкового розподілу в межах області, дуже корисним є аналіз відношень між сусідніми точками. Найчастіше це робиться іншим методом аналізу точкових розподілів – аналізом найближчого сусіда. Він передбачає здійснення процедури визначення відстані від кожної точки до її найближчого сусіда і порівняння цієї величини з середньою відстанню між сусідами. Обчислення цього статистичного показника включає визначення середнього (відстані до найближчого сусіда) серед всіх можливих пар найближчих точок. Середнє значення дає міру кількості точок в розподілі (області). Це корисно для аналізу відносин між об’єктами.
Як і в аналізі квадратів, ми можемо порівнювати значення відстані до найближчого сусіда з трьома можливими випадками розподілу – регулярним, випадковим, кластерним. У загальному випадку обчислюється значення індексу, з яким порівнюються власні результати. Точковий розподіл може також характеризуватися за допомогою полігонівТиссена, які ще називають діаграмами Диріхле і діаграмами Вороного. Вони базуються на ідеї, що ми можемо нарощувати полігони біля точок, щоб показати їх можливі зони впливу на інші точки покриття. Розмір точки, наприклад, міста – напряму пов’язаний з силою такого впливу. Розглянемо випадок, коли точки мають рівний вплив. Створення полігонів Тиссена дуже просто концептуально, але можуть бути ускладнення, коли кількість точок велика. Потрібно зрозуміти, що кожна точка оточена одиноким неправильним многокутником. Але многокутник має важливу властивість – будь-яка точка в середині нього знаходиться ближче до окремої точки, ніж будь-яка інша точка покриття. І навпаки, кожна точка зовні полігону ближче до деякої, ніж до окресленої. Іншими словами, границя кожного полігону дає оточеній точці найменшу можливу область впливу. Кожна точка буде мати свій власний полігон Тиссена, що показує зону її власного впливу. Розглянемо приклад. Утворення полігонів Тиссена можна подати як результат збільшення мильних кульок з центром у кожній точці. Наприкінці, межі кульок перетворюються в прямі лінії, а самі кульки – в многокутники. Сторони цих многокутників орієнтовані перпендикулярно лініям, що з’єднують сусідні точки. При чому, довжина двох відрізків, які утворилися з обох сторін границі – однакові (рис.4.25).
Алгоритми створення полігонів Тиссена відпрацьовані як для векторних так і для растрових геоінформаційних систем та використовуються для аналізу окремих областей (регіонів), які основані на наявних точкових об’єктах. Розподіл полігонів. Ми можемо аналізувати розподіл полігонів подібно тому, як це робили з точками – через визначення щільності полігонів на одиницю площі нашої області, яку вивчаємо. Однак при визначенні міри щільності полігонів ми повинні спочатку виміряти площу полігонів кожного класу, з тих, що нас цікавлять. Потім, потрібно сумарну площу кожного типу полігонів поділити на загальну площу покриття. Це дає нам значення відносної кількості полігонів (а не їх кількість на одиницю площі). Крім щільності полігонів, нас може цікавити їх розміщення і форма розподілу, яка утворюється групами полігонів. Але перед тим, як розглянути взаємодію полігональних об’єктів, ми повинні дізнатися, як вони можуть бути розміщені. Які точки, області (полігони) можуть бути згруповані, розсіяні регулярно, або випадковим чином по відношенню один до одного. Крім того, площинні об’єкти можуть бути з’єднанні один з одним, або перенесені на деяку відстань відносно один одного. Статистик з’єднань. При роботі з полігонами, у нас може виникнути потреба створення бінарних карт (карти на яких є тільки дві категорії полігонів). Для цього потрібно виконати розміщення всіх полігонів у двох великих класах (групах). Як нам відомо, умовою контакту полігональних об’єктів є їх суміжність. Хоча суміжність корисна для розгляду полігонів одного типу, які об’єднуються, але вона нам нічого не каже про розподіл, який утворює цей новий регіональний полігон. Для цього використовують статистичний показник (статистик) з’єднань (спільних границь).
З’єднання – це спільна границя двох суміжних полігонів. Статистик з’єднань підраховує кількість з’єднань в полігональному розподілі і характеризує структуру з’єднань кожного полігону. Розглянемо приклад. В нас є область з 15 полігонів (полігони двох типів: чорні та білі). Всього між ними може бути 22 з’єднання (рис.4.26).

Серед цих з’єднань можливі наступні: у випадку А) з’єднань між чорними полігонами - 8; між білими - 11; між білими та чорними -4); у випадку Б) з’єднань між білими полігонами - 2; між чорними та білими - 21; у випадку В) з’єднань між чорними полігонами - 5; між білими - 5; між чорними та білими полігонами - 13. Таким чином, ми маємо справу з випадками, коли мають місце наступні типи розподілів. Випадок а) кластерний (згрупований) розподіл; б) розріджений (нерівномірний) розподіл; в) випадковий розподіл. На цьому прикладі ми визначили кількість однорідних та різнорідних з’єднань і можемо визначити три різних класи розподілів (в залежності від випадків). Але як в дійсності порівняти результати аналізу однієї бази даних з тим, що можливо очікувати при кластерному, нерівномірному і випадковому розподілі. При аналізі точкових розподілів для оцінки випадковості ми зверталися до використання критерію c2. Але цей показник передбачає, що ми знаємо яким повинен бути розподіл, що очікується нами в умовах випадковості. Як би ми знали подібні розподіли для полігонів (на основі чисел з’єднань), то мали б можливість порівняти їх таким же чином. На практиці для встановлення значення розподілу з’єднань, що очікується, використовують два підходи. Перший – вільний відбір. Він передбачає, що ми можемо визначити частоту з’єднань, що очікується, на основі теоретичного знання ситуації, що моделюється, або виходячи з відомих розподілів. Другий підхід – обмежений підхід. В ньому не роблять теоретичних припущень про характер розподілу і не виконується порівняння кількості з’єднань підобласті (полігону) і всієї області (регіону). Він передбачає порівняння кількості з’єднань випадкового розподілу, що оцінюється, з кількістю з’єднань розподілу полігонів, що спостерігаються. Іншими словами, ми створюємо випадковий розподіл, виходячи з самих полігонів. Тоді ми маємо можливість порівняти наявні результати з випадковим розподілом.
Як за допомогою вільного, так і обмеженого відбору можливо подати сутність розподілу. Але для цього необхідний досвід роботи з геоінформаційними системами. Крім того, на практиці, під час аналізу полігонів використовують: міру полігональної ізольованості; міру доступу; міру взаємодії полігонів; міру розосередженості.
Розподіл ліній. Завдання виконання просторового аналізу за допомогою геоінформаційної системи часто потребує аналізу лінійних об’єктів та зв’язків між ними. Тому потрібно розглянути основні види розподілу лінійних об’єктів, з якими користувач може зустрітися на практиці. Щільність ліній. Оскільки лінії на відміну від точок мають просторову протяжність то аналіз їх розподілів більш складніший. Першою мірою розподілу ліній є щільність ліній. Вона є відношенням добутку їх довжини (ліній) до площі покриття. Виражається цей показник у метрах на га, або км на км2. Але крім порівняння отриманих значень щільності ліній станом на деякий час, цей показник має малу користь. Тому використовують інші показники розподілу ліній, відповідно тому, як це було розглянуто з розподілом точок і полігонів. Найближчі сусіди і перетини ліній. Розподіл пар ліній може бути визначений таким же чином, як ми працювали з точками, але визначення ускладнюється, так як лінії мають розмірність (довжину). Однак, внаслідок того, що лінії мають різну довжину, отримані дані не дадуть правдивої картини розподілу ліній. З точки зору статистики часто корисним вважається робити випадкову вибірку. Вона передбачає визначення випадкової точки на кожній лінії карти (точка Б, рис. 4.27). Далі, проводиться перпендикуляр з цієї точки до найближчої лінії. Потім ми вимірюємо ці відстані і підраховуємо середню відстань до найближчого сусіда.
Для обчислення відношення добутку довжин ліній на площу використовують формулу:
де: n – кількість ліній; L – добуток довжини ліній; А – площа. Ця скоректована щільність ліній покращить якість статистика найближчого сусіда. Методи перетину ліній. Ці методи є альтернативою при аналізі розподілу ліній. Сутність підходу полягає у тому, щоб перетворити двомірний простір об’єктів в одновимірну послідовність кресленням вибіркової лінії через карту і урахуванням перетину цієї лінії з лініями покриття. На практиці є два способи створення таких ліній.
Перший спосіб – випадково вибрати дві точки та поєднати їх лінією. Другий спосіб – полягає у проведенні променя з випадкової точки під випадковим кутом, відкладанні випадкової відстані від початкової точки і проведенні перпендикуляру до променя з цієї точки. Після того, як лінія проведена, можна розглянути розподіл інтервалів між точками перетину її з лініями покриття на основі використанням стандартних методів аналізу даних. Альтернативою одинокої лінії є ломана лінія, яка перетинає покриття два чи три рази. Такий шлях (називають випадковим обходом) також створює серію перетинів, відстані між якими можуть бути проаналізовані будь-яким статистичним методом для послідовностей даних (рис.4.28).
Напрям лінійних і площинних об’єктів. Лінійні об’єкти можуть характеризуватися не тільки розподілом за ландшафтом місцевості, але і своєю орієнтацією. Під час аналізу орієнтації, може виникнути ситуація вибору між двома зустрічними напрямками. Якщо лінійний об’єкт є вулицею з одностороннім рухом, то орієнтація вулиці не говорить про напрямок, в якому повинен рухатися транспорт. Тому нам ще крім орієнтації необхідно знати і про напрямок. Ми можемо розглядати розподіл лінійних об’єктів або як двовимірний, або як трьохвимірний, з урахуванням кутового напрямку відносно поверхні сфери. В традиційному статистичному аналізі, орієнтація ліній з карти переноситься на діаграму напрямків, де всі вони накреслені з однієї початкової точки. Діаграми напрямків корисні для візуальної оцінки, але виміри, отримані безпосередньо за даними покриття більше підходять для чисельного аналізу. За допомогою отриманих значень напрямків лінійних і площинних об’єктів можливо охарактеризувати розподіл всередині покриття та порівняти їх з даними інших покриттів для встановлення механізму змін. Зв’язаність лінійних об’єктів. Важливим аспектом просторового розміщення ліній є їх здатність утворювати мережу. Мережі мають різноманітні форми і мірою складності мережі є її зв’язаність. Існує кілька методів для визначення цієї характеристики і найбільш загальними є: гамма-індекс та альфа-індекс. Гамма-індекс (g) - є відношення кількості існуючих зв’язків між парами вузлів мережі (L) до максимально можливої кількості зв’язків у тому ж наборі вузлів (L max). Значення L max визначається за формулою: L max = 3 (V - 2), (4.10) де: V – кількість вузлів. Тоді значення гамма-індексу визначається за формулою: g = L/L max = L / 3 (V - 2). (4.11) Значення гамма-індексу може приймати величину від 0 – зв’язків немає до 1 – всі можливі зв’язки присутні. Чим більше зв’язків в мережі, тим спрощено переміщення по ній.
а) g=15: 3 (16-2) = 0.36 б) g = 20: 3 (16-2) = 0.48
Важливою характеристикою мережі крім зв’язаності є наявність в ній контурів, які дозволяють переміщуватися від вузла до вузла різними маршрутами. В якості міри об’єднаності вузлів контурами альтернативних матеріалів використовується альфа-індекс (a). Він є відношенням наявного в мережі числа контурів до максимального можливого числа контурів в цій мережі. Відомо, що мережа без контурів має зв’язків на одиницю менше ніж, кількість вузлів: L = V – 1. (4.12) На рис. 4.29 а) маємо 16 вузлів і 15 зв’язків. Максимальна кількість зв’язків в мережі визначається як 3(V - 2), а мінімальна (без втрати зв’язаності) як (V – 1), тоді максимальна кількість контурів буде [3(V - 2) - (V - 1)], тобто (2V – 5). В такому випадку, альфа-індекс буде обчислений за формулою: a = (L - (V - 1))/(2V - 5). (4.13) Діапазон значень альфа-індекс знаходиться в межах від 0 – мережа без контурів до 1 – мережа з максимальною кількістю контурів. Підрахуємо значення a - індексу для варіантів а) і б) - рис 4.29. a = (15 - 16 + 1) / (2 ´ 16 - 5) = 0 a = (20 - 16 + 1) / (2 ´ 16 - 5) = 0.19 Таким чином, в мережі на рис. 4.29 - а) можливий тільки один варіант для переміщення з однієї точки в іншу, а на рис. 4.29 - б) можливі кілька варіантів різної довжини маршруту переміщення. Длямоделювання транспортних мереж нам потрібно знати більше, ніж параметри зв’язаності. Тут важливе значення мають довжини зв’язків між вузлами, можливі напрямки руху по цим лініям, значення опору руху тощо. Крім того, важливе значення будуть мати кількість альтернативних маршрутів між визначеними вузлами, пошук центрального вузла (вузол, що має найбільшу кількість зв’язків). Все це можливо поєднувати між собою та з іншими даними – розміщенням, орієнтацією ліній – для отримання більш повної картини мережі. Модель гравітації. На практиці, окремі вузли можуть мати різну роль. Нам відомо, що більш великі об’єкти залучають до себе більш активності. Розмір такого тяжіння може подаватися подібно гравітаційному тяжінню тіл, які мають певну масу. Чим більше маса, тим більше сила тяжіння між тілом і його сусідами. Здійснивши переміщення ідеї тяжіння на взаємодію між вузлами покриття геоінформаційної системи, ми отримаємо модель гравітації, яка в загальному виді виражається:
де: Lij – величина взаємодії між вузлами i та j; Рi – величина вузла і; Рj – величина вузла j; d – відстань між вузлами; К – константа, що визначається природою об’єктів, які взаємодіють. Величини вузлів можуть бути подані параметрами: потреба в продукції, площа об’єкта, обсяг виробництва, продаж, тощо. Чим більше величини вузлів, тим більша сила взаємодії між ними і, зі збільшенням відстані між вузлами сила взаємодії зменшується. В загальному випадку модель гравітації застосовується для аналізу потоків між вузлами різної величини. Маршрутизація і аллокація. Серед найбільш поширених задач аналізу мереж, що використовуються в геоінформаційних системах, є задачі маршрутизації та аллокації. Найпростіший варіант маршрутизації полягає в пошуку найкоротшого маршруту між двома вузлами мережі (рис. 4.30).
Враховуючи, що кожний вузол може мати свій ваговий коефіцієнт, можливий варіант маршрутизації від визначеної точки до найближчої точки з максимальною вагою. Крім того, кожний зв’язок в мережі може мати значення опору руху. Використовуючисумарну відстань з урахуванням геометричної відстані, так і значення опору руху, можливо побудувати найбільш ефективний маршрут, а не просто найкоротший. Необхідно пам’ятати, що вузлам також можуть бути присвоєні значення опору руху і їх значення потрібно обов’язково враховувати під час обчислення. Досвід використання ГІС свідчить, що хоча маршрутизація може виконуватися на растровій моделі, але вона більш легко реалізується на векторній моделі даних.
Необхідно відмітити ще одну властивість, яка використовується при вирішенні завдань аналізу за допомогою ГІС. Це – зв’язок поштових адрес з лінійними об’єктами, які утворюють покриття вуличної мережі. Встановлення такої відповідності називається адресним геокодуванням. Воно дозволяє визначити поштову (логічну) адресу за географічними або умовними координатами в мережі, а також виконати обернені перетворення. Його необхідність обумовлена тим, що люди використовують логічні адреси, в той же час як геоінформаційна система оперує з координатами і топологією. І на закінчення, необхідно відмітити наступне. Ми розглянули точкові, лінійні та площинні об’єкти. Ми їх можемо дослідити на предмет їх розподілу, зв’язку, орієнтації тощо. Однак усі ці аналітичні операції мають потребу тільки при співвідношенні їх з аналізом інших покрить, що дозволяє встановити причинні механізми явищ та процесів, які ми розглядаємо за допомогою геоінформаційної системи, і визначити вплив одних об’єктів на інші.
Питання.
1. Атрибути об’єктів, для чого вони використовуються? 2. Назвіть основні характеристики лінійних об’єктів? 3. Назвіть основні характеристики площинних об’єктів? 4. Сутність геометричних об’єктів високого рівня, їх класифікація та характеристика? 5. Що таке центроїди, їх види. Як їх знайти у векторній геоінформаційній системі? 6. Що таке мережа. Які існують види мереж? 7. Особливості вимірювання лінійних та площинних об’єктів за допомогою геоінформаційної системи? 8. Особливості вимірювання відстаней за допомогою геоінформаційної системи? 9. Що таке поверхня. Види поверхонь та способи їх подання? 10. Основні методи отримання значень висот точок поверхні? 11. Цифрова модель місцевості, її сутність та використання в геоінформаційних системах? 12. Існуючі види аналізу поверхні. Їх сутність? 13. Основні фактори, що впливають на точність інтерполяції поверхні? 14. Просторовий розподіл, його сутність. Основні види розподілу? 15. Особливості аналізу розподілу полігонів? 16. Особливості аналізу розподілу ліній? 17. Модель гравітації, її сутність. Особливості її використання для вирішення завдань аналізу? 18. Сутність маршрутизації та аллокації. Їх використання в геоінформаційних системах при вирішенні завдань аналізу мереж? 19. В чому полягає сутність адресного геокодування?
________________
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.66.165 (0.016 с.) |

 , (4.8)
, (4.8)

 , (4.9)
, (4.9)
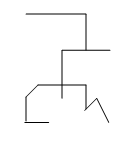

 , (4.14)
, (4.14)
 Аллокація – це процес визначення місця розташування об’єкта з встановленими властивостями (магазин, станція очищення води тощо) або границь зони обслуговування певним об’єктом (рис.4.31). Найчастіше для цього використовується мережева структура у векторній геоінформаційній системі. Сутність вирішення цього завдання полягає у розповсюдженні можливостей певної служби по мережі. Кожний зв’язок (або кожний вузол) мережі має встановлену кількість елементів, які обслуговуються. Крім того, кожна служба має встановлену максимальну завантаженість та граничну відстань обслуговування, а термінові служби – обмеження на час з обслуговування одного звернення – все це повинно бути враховано. В тому випадку, коли б мережа шляхів була однорідна (відсутні: опір руху, обмеження, заперечення), то аллокація була б простою справою (вибір критерію і розширення зон обслуговування від центру, поки суміжні границі не зустрінуться). Але більшість задач аллокації більш складні, так як враховують різні обмеження.
Аллокація – це процес визначення місця розташування об’єкта з встановленими властивостями (магазин, станція очищення води тощо) або границь зони обслуговування певним об’єктом (рис.4.31). Найчастіше для цього використовується мережева структура у векторній геоінформаційній системі. Сутність вирішення цього завдання полягає у розповсюдженні можливостей певної служби по мережі. Кожний зв’язок (або кожний вузол) мережі має встановлену кількість елементів, які обслуговуються. Крім того, кожна служба має встановлену максимальну завантаженість та граничну відстань обслуговування, а термінові служби – обмеження на час з обслуговування одного звернення – все це повинно бути враховано. В тому випадку, коли б мережа шляхів була однорідна (відсутні: опір руху, обмеження, заперечення), то аллокація була б простою справою (вибір критерію і розширення зон обслуговування від центру, поки суміжні границі не зустрінуться). Але більшість задач аллокації більш складні, так як враховують різні обмеження.


