Расчет магнитной цепи с двумя узлами
Похожие статьи вашей тематики
В электротехнических устройствах часто встречаются магнитные цепи, сердечники которых выполнены из листовой электротехнической стали в виде трех ветвей с двумя узлами. Рассмотрим порядок расчета такой магнитной цепи, схематически изображенной на рис. 11.24,а.
Пример 11.7
Известны геометрические размеры сердечника и характеристика его материала. Сердечник выполнен из листовой электротехнической стали, основная кривая намагничивания которой приведена на рис. 11.24,б. Площадь сечения 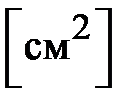 сердечника в крайних стержнях составляет сердечника в крайних стержнях составляет 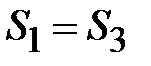 , а в среднем стержне – , а в среднем стержне –  . На крайних стержнях длиной . На крайних стержнях длиной 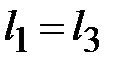 [см] находятся обмотки с числом витков [см] находятся обмотки с числом витков 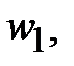 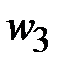 и токами и токами 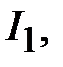 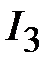 [A]. В среднем стержне длиной [A]. В среднем стержне длиной 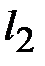 имеется воздушный зазор толщиной имеется воздушный зазор толщиной 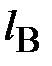 . .
Требуется определить магнитные потоки в каждом из стержней.
Решение
1. Разбиваем цепь на участки и подсчитываем их длины и площади сечений.
В крайних стержнях имеется только по одному участку с одинаковыми сечением и длиной. В среднем стержне два участка: воздушный зазор и примыкающие к нему части второго стержня из стали. Параметры участков сведены в табл. 11.3.
Таблица 11.3
| Номер
участка k
| 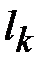
| 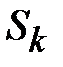
| Материал
| | см
| 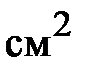
| |
| 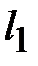
| 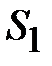
|
Сталь
| |
| 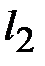
| 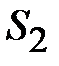
| |
| 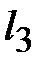
| 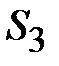
| |
| 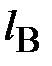
| 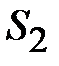
| Воздух
| 
2. Составляем схему замещения магнитной цепи (рис. 11.25) и определяем ее параметры:
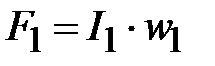 [A], [A], 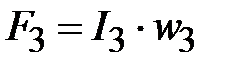 [A], [A], 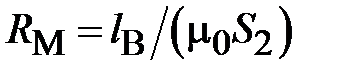 [1/Гн]. [1/Гн].
3. Записываем уравнения ВбАХ ветвей и всей схемы соответственно по второму и первому законам Кирхгофа для магнитной цепи:
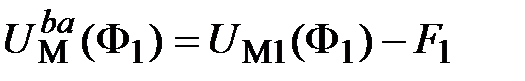 ;(11.12) ;(11.12)
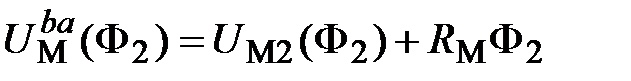 ; (11.13) ; (11.13)
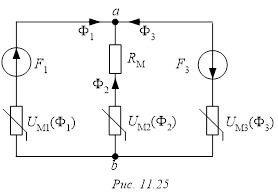 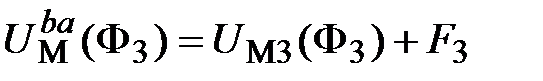 ;(11.14) ;(11.14)
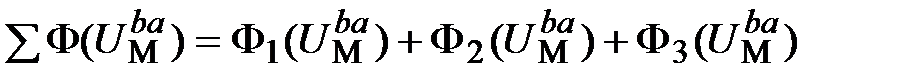 ;(11.15) где при k = 1, 2, 3 имеем ;(11.15) где при k = 1, 2, 3 имеем 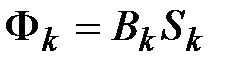 , (11.16) , (11.16)
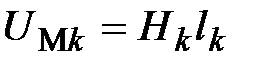 . (11.17) . (11.17)
4. Задаваясь значениями магнитной индукции 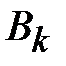 [Тл] по формуле (11.16) находим магнитные потоки [Тл] по формуле (11.16) находим магнитные потоки 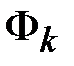 [Вб]. Затем по кривой намагничивания B (H) определяем [Вб]. Затем по кривой намагничивания B (H) определяем 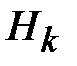 [ [ 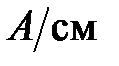 ]. После этого вычисляем ]. После этого вычисляем 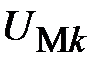 [A] по формуле (11.17) и, наконец, по формулам (11.12–11.14) находим значения [A] по формуле (11.17) и, наконец, по формулам (11.12–11.14) находим значения 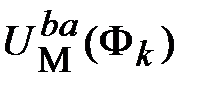 . .
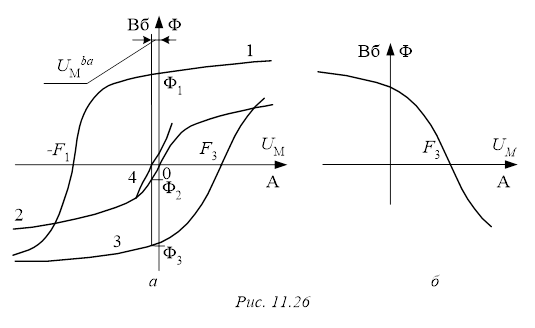
5. По результатам вычислений строим ВбАХ ветвей (кривые 1, 2, 3 на рис. 11.26,а – нумерация соответствует нумерации магнитных потоков). Затем строим и характеристику всей цепи (кривая 4 на рис. 11.26,а), складывая потоки при одних и тех же значениях узлового магнитного напряжения 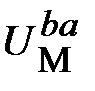 . Абсцисса точки пересечения эквивалентной характеристики с осью напряжений ( . Абсцисса точки пересечения эквивалентной характеристики с осью напряжений (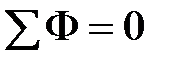 ) дает значение ) дает значение 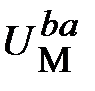 , а ординаты точек на ВбАХ ветвей, соответствующие этому напряжению – значения магнитных потоков , а ординаты точек на ВбАХ ветвей, соответствующие этому напряжению – значения магнитных потоков 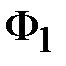 , , 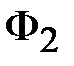 , , 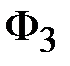 в стержнях. в стержнях.
Примечания
1. Обратим внимание, что если в уравнении ВбАХ ветви к магнитному напряжению участка добавляется МДС + F, как в (11.14), то ВбАХ участка смещается параллельно самой себе вправо вдоль оси U М. А если МДС вычитается, то ВбАХ смещается влево.
2. Характеристика ветви с воздушным зазором более полога.
3. Если один из магнитных потоков, например, Ф3 направлен от узла а к узлу b, то уравнение (11.4) примет вид: U М ba (Ф3)= – U М3(Ф3) + F 3. Соответствующая ВбАХ участка зеркально отображается относительно оси Ф и смещается на величину F 3 (рис 11.26,б).
В схеме рис. 11.24 есть лишь один воздушный зазор, поэтому можно ограничиться построением лишь одной кривой 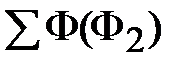 , изменив порядок расчета. , изменив порядок расчета.
 Зададимся произвольным значением потока Зададимся произвольным значением потока 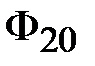 . По формуле (11.16) вычислим . По формуле (11.16) вычислим 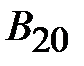 . По основной кривой намагничивания (рис. 11.24,б) найдем . По основной кривой намагничивания (рис. 11.24,б) найдем 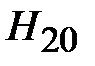 . Затем по формуле (11.17) подсчитаем . Затем по формуле (11.17) подсчитаем 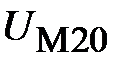 , а по формуле (11.13) – , а по формуле (11.13) –  . Зная последнее, по формулам (11.12 и 11.14) найдем . Зная последнее, по формулам (11.12 и 11.14) найдем 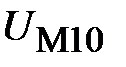 и и 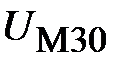 соответственно. Затем, используя (11.17), подсчитаем величины соответственно. Затем, используя (11.17), подсчитаем величины 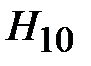 и и 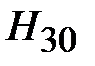 , а по кривой В (Н) определим соответствующие им значения , а по кривой В (Н) определим соответствующие им значения 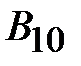 и и 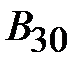 . После этого вычислим . После этого вычислим 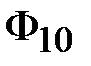 и и 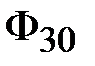 по формуле (11.16). Суммируя все три магнитных потока, найдем по формуле (11.16). Суммируя все три магнитных потока, найдем 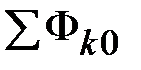 . .
Теперь в осях 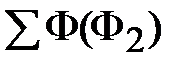 нанесем точку 0, абсцисса которой равна нанесем точку 0, абсцисса которой равна 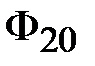 , а ордината – , а ордината – 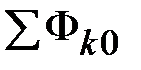 (рис. 11.27). Обнаружив, что (рис. 11.27). Обнаружив, что 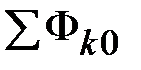 не равна нулю, зададимся другим значением магнитного потока в среднем стержне не равна нулю, зададимся другим значением магнитного потока в среднем стержне 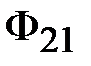 и повторим расчет, определив и повторим расчет, определив 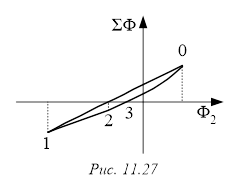 новое значение суммы потоков новое значение суммы потоков 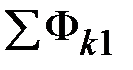 . Если и в этом случае . Если и в этом случае 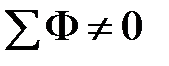 , то нанесем на график , то нанесем на график 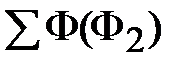 новую точку 1. Соединим отрезком прямой точки 1 и 0. Определим координату новую точку 1. Соединим отрезком прямой точки 1 и 0. Определим координату 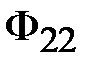 точки пересечения этого отрезка с осью абсцисс и вновь повторим расчет, вычислив точки пересечения этого отрезка с осью абсцисс и вновь повторим расчет, вычислив 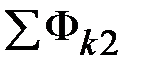 . Нанесем на график соответствующую точку 3. Если и она не окажется на оси абсцисс, то через точки 0, 1, 2 проведем плавную кривую и определим координату . Нанесем на график соответствующую точку 3. Если и она не окажется на оси абсцисс, то через точки 0, 1, 2 проведем плавную кривую и определим координату 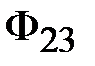 точки ее пересечения с осью абсцисс. Очередное повторение расчета дает, как правило, результат точки ее пересечения с осью абсцисс. Очередное повторение расчета дает, как правило, результат 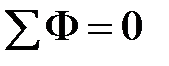 с удовлетворительной степенью точности. с удовлетворительной степенью точности.
Таким образом, используя метод последовательных приближений, можно получить решение с меньшим количеством вычислений и построений.
|