

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Методика составления уравнений состояния на основе принципа наложения
 Данная методика составления уравнений состояния вытекает из разделения исходной цепи на две подсхемы: Данная методика составления уравнений состояния вытекает из разделения исходной цепи на две подсхемы:
- первая включает в себя элементы, запасающие энергию, а также нелинейные резистивные элементы и источники питания;
-вторая охватывает линейные резистивные элементы.
Пример такого представления исходной цепи приведен на рис. 1,а, где пассивный многополюсник П соответствует второй подсхеме.
 Следующий этап рассматриваемой методики заключается в замене на основании теоремы о компенсации всех конденсаторов, а также нелинейных резистивных элементов с характеристикой типа u(i) источниками напряжения, а всех катушек индуктивности и нелинейных резистивных элементов с характеристикой типа i(u) – источниками тока (рис. 1,б). В результате исходная цепь трансформируется в резистивную, в которой, помимо заданных (независимых) источников, действуют управляемые источники. Следующий этап рассматриваемой методики заключается в замене на основании теоремы о компенсации всех конденсаторов, а также нелинейных резистивных элементов с характеристикой типа u(i) источниками напряжения, а всех катушек индуктивности и нелинейных резистивных элементов с характеристикой типа i(u) – источниками тока (рис. 1,б). В результате исходная цепь трансформируется в резистивную, в которой, помимо заданных (независимых) источников, действуют управляемые источники.
На третьем этапе с использованием метода наложения определяются выражения входных токов и напряжений пассивного многополюсника П через напряжения и токи всех присоединенных к нему источников.
В качестве примера составим уравнения состояния для цепи на рис. 2,а и определим выражения  и и  . .
1. В соответствии с изложенной методикой заменим исходную цепь схемой замещения на рис. 2,б. На основании метода наложения этой схеме соответствует пять цепей, приведенных на рис. 3. С их использованием для тока  =dq/dt в ветви с конденсатором и напряжения =dq/dt в ветви с конденсатором и напряжения  на зажимах катушки индуктивности запишем на зажимах катушки индуктивности запишем
  
 2. Выражение для искомого напряжения 2. Выражение для искомого напряжения  определяется согласно закону Ома: определяется согласно закону Ома: 
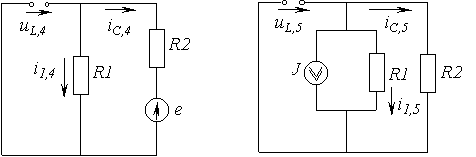  На основании метода наложения с использованием расчетных схем на рис. 3 для второй искомой переменной – тока На основании метода наложения с использованием расчетных схем на рис. 3 для второй искомой переменной – тока  запишем запишем
 
3. Объединив (2)  (5) с учетом (5) с учетом  , получим матричное уравнение вида (1): , получим матричное уравнение вида (1):
  
Вектор начальных значений   = =   . .
Сравнивая в заключение рассмотренные методики составления уравнений состояния, можно отметить, что методика, основанная на использовании принципа наложения, не содержит достаточно сложного этапа исключения переменных резистивных ветвей из уравнений состояния, входящего в методику составления уравнений на основе таблицы соединений. Вместе с тем использование метода наложения для сложных цепей может также оказаться весьма трудоемкой задачей.
Метод дискретных моделей
Метод основан на использовании дискретных моделей индуктивного и емкостного элементов и позволяет свести численный анализ динамических процессов в нелинейных цепях к последовательному расчету на каждом шаге нелинейных резистивных цепей.
Дискретные модели вытекают из неявных алгоритмов, в частности из обратной формулы Эйлера. Эти модели, полученные на основе неявного алгоритма Эйлера, а также выражения для параметров входящих в них элементов приведены в табл. 1.
Таблица 1. Дискретные модели индуктивного и емкостного элементов
| Тип элемента
| Аналитические
соотношения
| Дискретная модель
| Индуктивный элемент

| Емкостный элемент

| | | 
| Примечание: если емкостный и индуктивный элементы линейные и  то то  и и 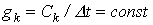 . .
Метод дискретных моделей хорошо поддается машинной алгоритмизации и используется для расчета сложных нелинейных цепей на ЭВМ. Для достаточно простых схем он может быть реализован ’’вручную’’.
Последовательность расчета нелинейной цепи методом дискретных моделей иллюстрируется приведенным ниже примером решения задачи.
В цепи на рис. 3 предыдущей задачи ЭДС источника Е = 1В;  1Ом; 1Ом;  4 Ом. Вебер - амперная характеристика нелинейной катушки индуктивности аппроксимирована выражением 4 Ом. Вебер - амперная характеристика нелинейной катушки индуктивности аппроксимирована выражением  где ток – в амперах, потокосцепление – в веберах. где ток – в амперах, потокосцепление – в веберах.
Рассчитать ток i в цепи после замыкания ключа
 Решение Решение
1. Нарисуем расчетную дискретную схему замещения цепи (см. рис. 4).
Для этой схемы справедливо 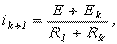 где в соответствии с табл. 1 где в соответствии с табл. 1 
Значение дифференциальной индуктивности нелинейной катушки на k-м шаге 
2. Выберем шаг интегрирования  На основании закона коммутации На основании закона коммутации   Тогда Тогда  и в соответствии с (7) и в соответствии с (7)  . Параметры элементов схемы замещения: . Параметры элементов схемы замещения: 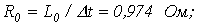 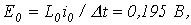 откуда на основании (6) откуда на основании (6) 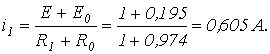 На следующем шаге На следующем шаге  тогда тогда  и параметры элементов схемы замещения и параметры элементов схемы замещения    откуда откуда  . Результаты пошагового расчета согласно приведенному алгоритму представлены в табл. 2. Таблица 2. Результаты расчета . Результаты пошагового расчета согласно приведенному алгоритму представлены в табл. 2. Таблица 2. Результаты расчета

| 
| 
| 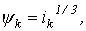
| 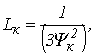
| 
| 
| 
| |
| с
| А
| Вб
| Гн
| Ом
| В
| А
| |
|
| 0,2
| 0,585
| 0,974
| 0,974
| 0,195
| 0,605
| |
|
| 0,605
| 0,846
| 0,466
| 0,466
| 0,282
| 0,874
| |
|
| 0,874
| 0,956
| 0,365
| 0,365
| 0,319
| 0,966
| |
|
| 0,966
| 0,989
| 0,341
| 0,341
| 0,329
| 0,99
| |
|
| 0,99
| 0,997
| 0,335
| 0,335
| 0,332
| 0,998
|
Исходные данные для любого метода численного исследования.
|