
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод составления и решения уравнений Кирхгофа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Положим, что в схеме, содержащей "m" ветвей к "n" узлов, заданными являются все элементы и конфигурация, а искомыми - токи в ветвях. Число неизвестных при этом равно числу ветвей.
1). Выбираем произвольно положительные направления токов в ветвях (удобно в ветвях с источниками напряжений направить токи по стрелке эдс). 2). Составляем уравнения 1-го закона Кирхгофа. Возможно составление "n" уравнений вида. Нетрудно заметить, что каждый ток войдет в два уравнения с противоположными знаками. Поэтому сумма уравнений тождественно равна нулю, т.е. одно из уравнений вытекает из n-1 остальных. Следовательно, по 1-му закону Кирхгофа необходимо составить n – 1 независимых уравнений. 3). Недостающие для определения "m" неизвестных токов уравнения должны быть записаны по 2-ому закону Кирхгофа. Их необходимо иметь m - (n - 1) = m - n + 1. Если ко всем ветвям применить закон Ома, то получится "m" уравнений вида: В систему уравнений закона Ома входят "m" неизвестных токов Ik и n-1 неизвестных потенциалов (потенциал одного узла принимается равным нулю). Если исключить эти неизвестные потенциалы, останется m - n + 1 уравнений, связывающих эдс источников с напряжениями на сопротивлениях, т. е. уравнения 2-го закона Кирхгофа. Для того, чтобы уравнения были независимыми, необходимо, чтобы в каждое последующее входила хотя бы одна новая ветвь. Практически удобно записывать уравнения для контуров, не имеющих внутри ветвей, т. е. для ячеек. 4). Количество необходимых уравнений 1-го и 2-го законов Кирхгофа легко устанавливается по графу цепи. Для этого составляется дерево графа. Ранее установлено, что число ветвей дерева графа как раз равно n - 1, т. е. равно числу необходимых и достаточных уравнений 1-го закона Кирхгофа. Число необходимых и достаточных уравнений 2-го закона Кирхгофа m - n + 1 равно числу ветвей связи. 5). При расчете цепей часто определяется мощность источников и приемников энергии. Следует учитывать, что должен соблюдаться закон сохранения энергии, вследствие которого В левой части уравнения при совпадении направлений Еh и Ih произведение положительно, а при несовпадении- отрицательно.
6). При наличии в схеме источников тока их следует учитывать при записи уравнений 1-го закона Кирхгофа. Отдаваемая ими энергия учитывается в левой части уравнения баланса мощностей. 7). Если ток определен отрицательным, то его действительное направление противоположно принятому в начале расчета.
Исключим токи внутренних ветвей, выразив их через токи внешних Полученная система уравнений содержит три неизвестных I1 , I2 , I3 , через которые могут быть затем определены I4 и I5.
а) контурного тока данной ячейки на сумму сопротивлений контура; б) контурных токов каждой смежной ячейки - на сопротивления смежных ветвей. Правило знаков остается таким же, как и при записи уравнений 2-го закона Кирхгофа. Общий вид уравнений для "n" контуров: где Rnn - сумма сопротивлений n-ой ячейки, Rn2 - сумма сопротивлений ветви, общей для n-ого и 2-го контуров, Еn - алгебраическая сумма эдс n-ого контура. Полученная система может быть решена с помощью определителей:
Если схема содержит источники тока, то можно принять ток каждого замыкающимся по ветви любого незамкнутого контура, дополняющего ветвь с источником тока до замкнутого. Падение напряжения за счет такого тока на сопротивлении контура учитывается вместе с падением напряжений от контурных токов. Метод узловых потенциалов.
Выразим токи всех ветвей, примыкающих к узлу "а" по закону Ома: На основании 1-го закона Кирхгофа: Аналогичного вида уравнения могут быть получены для узла ‘b’, а также для любого узла более сложной схемы. Анализ уравнений показывает, что для любого узла алгебраическая сумма произведений эдс на проводимость всех подключенных к нему ветвей равна а) потенциалу данного узла, умноженному на сумму проводимостей подключенных к нему ветвей, б) минус произведение потенциалов остальных узлов, умноженных каждый на сумму проводимостей ветвей, соединяющих узел с тем, для которого пишется уравнение. Если эдс направлена к узлу, то EkGk входит в уравнения с "плюсом", от узла - с "минусом". Источники тока следует учитывать в левой части уравнений с "плюсом", если они направлены к данному узлу. Общий вид уравнений: Уравнения записываются для (n - 1) узлов и решаются, например, с помощью определителей. По полученным узловым потенциалам определяются токи ветвей с помощью закона Ома.
Решение системы линейных уравнений однозначно определяет токи. Предполагая поочередно в этой же цепи наличие только одной эдс при прочих равных нулю, можно для каждой эдс вычислить соответствующие токи ветвей, составив уравнения: для Е1, для Е2. и так далее. Сложив уравнения почленно, получим: Полученная система имеет единственное решение для неизвестных Из сравнения исходных уравнений и только что полученных следует, что решения должны совпадать, т.е.
На этом основан расчет цепей методом наложения. Напряжение на участке цепи с сопротивлением R: т.е. принцип наложения применим и к напряжениям. Принцип наложения применим также и к источникам тока. При этом остальные источники тока отключаются. Принцип наложения не применяется для мощностей - квадратичных функций токов и напряжений. Преобразование электрических цепей. Различные преобразования применяются обычно совместно с другими методами расчета. При этом цепь остается эквивалентной заданной, но расчет токов значительно упрощается. Принцип взаимности.
Согласно методу контурных токов:
Общие сопротивления R q l и Rl q. равны, т.к. R12 = R21, R23 = R32 и т.д. Поэтому
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.175.172 (0.009 с.) |

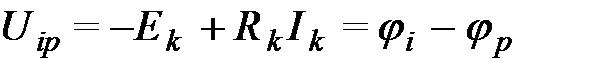 , где
, где 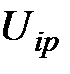 - напряжение между узлами i и р, Еk, Ik - эдс источника и ток в к-ой ветви, направленные от узла к узлу р, R - сопротивление к-ой ветви. Более удобна запись:
- напряжение между узлами i и р, Еk, Ik - эдс источника и ток в к-ой ветви, направленные от узла к узлу р, R - сопротивление к-ой ветви. Более удобна запись: 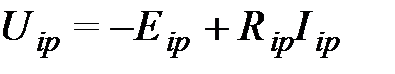 .
.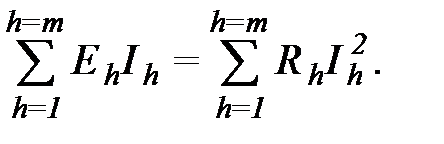
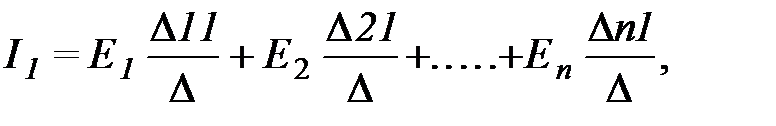
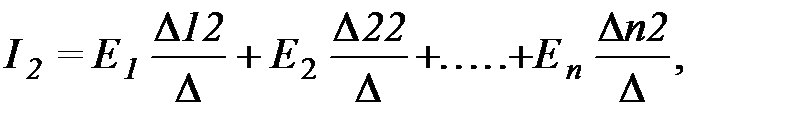
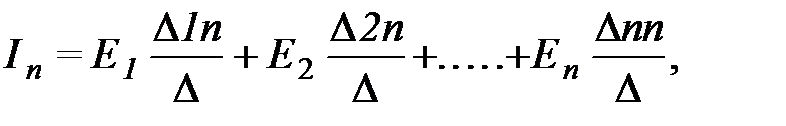 где
где 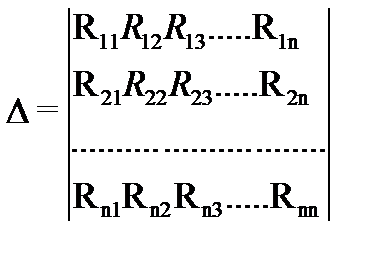 - определитель системы,
- определитель системы, 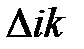 - алгебраическое дополнение, полученное из определителя системы умножением на
- алгебраическое дополнение, полученное из определителя системы умножением на  и исключением i -ой строки и k -гo столбца.
и исключением i -ой строки и k -гo столбца.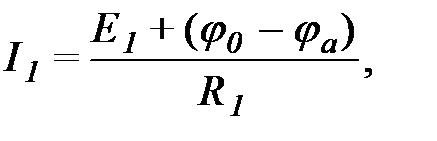
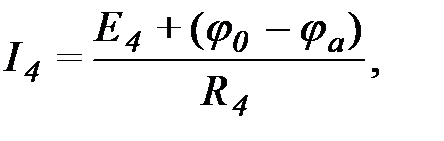
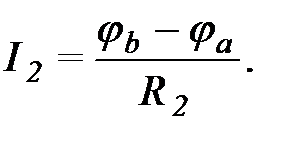
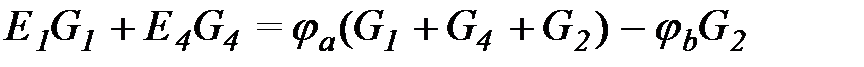 .
.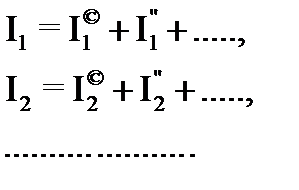
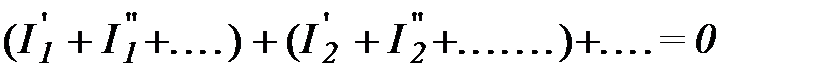 и т.д.
и т.д.
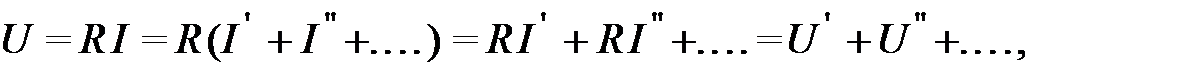

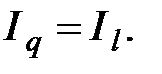
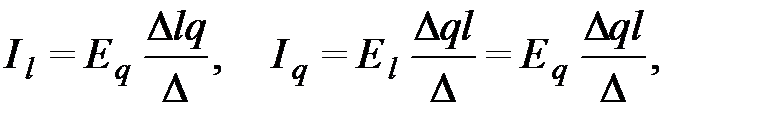 Так как для системы
Так как для системы 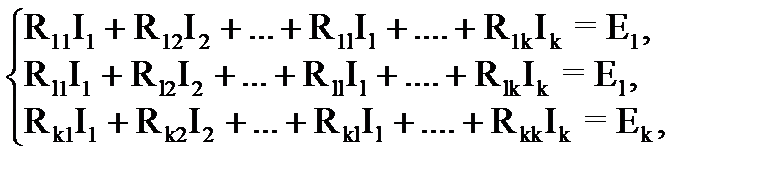 ток в ветви l определяется из
ток в ветви l определяется из 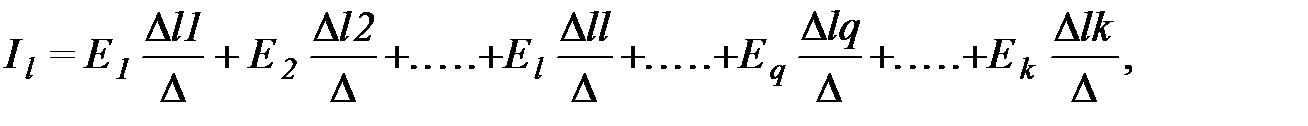 где
где 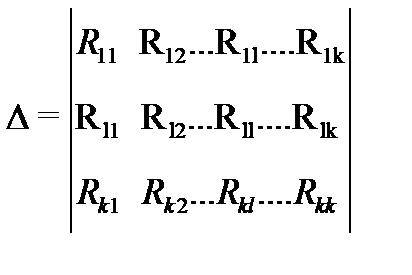 , а алгебраические дополнения вида
, а алгебраические дополнения вида 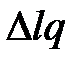 получаются из
получаются из  , путем вычеркивания l - столбца и q - строки и умножения полученного определителя на
, путем вычеркивания l - столбца и q - строки и умножения полученного определителя на 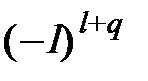 .
.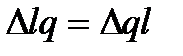 и отличается только тем, что строки
и отличается только тем, что строки 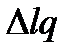 являются столбцами
являются столбцами 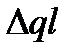 .Следовательно
.Следовательно 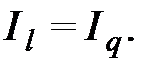 Принцип может быть применен, например, для определения токов в различных ветвях схемы при одной эдс.
Принцип может быть применен, например, для определения токов в различных ветвях схемы при одной эдс.


