
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решим для контроля эту же систему линейных уравнений с помощью программы Excel.Содержание книги
Поиск на нашем сайте
Итак, получаем следующее решение:
- Согласуется ли решение математической задачи условию прикладной задаче? - Решение удовлетворяет условию - Что для этого надо сделать? - Необходимо округлить значения неизвестных до целых, не учитывая правило округления. В результате получим: Проверка: - Сформулируйте полученный ответ согласно условию прикладной задачи. Ответ: для разрезания I способом нужно взять 43 прутка, II способом – 103 прутка, III – 42. Всего необходимо взять 43+103+42=188 прутков. При этом получим
- Возможно ли построение другой математической модели? - …….. Замечание: для производственных задач данного класса математической моделью является система линейных уравнений. - Возможно ли получение другого ответа? - Если воспользоваться другими способами разрезания из 10-ти рассмотренных, то получили бы другой ответ. Например, если взять 1, 3 и 10 способы разрезания, то получили бы следующую математическую модель
при дополнительном условии: В результате получили бы Этот случай менее экономичный, так как больше остается отходов.
Замечание: даже для построенной математической модели во втором случае можно получить несколько другой ответ. Если последовательно найти целочисленные значения Ответ: для разрезания I способом нужно взять 43 прутка, II способом – 103 прутка, III – 43. Всего необходимо взять 43+103+43=189 прутков. При этом получим
Задача 2 (задача линейных электрических цепей постоянного тока). В электрической цепи
Решение.
Данная задача относится к физическим задачам. Электрическая схема имеет два узла и три ветви. Для решения задачи используются законы Кирхгофа.
Расчет электрических цепей с помощью законов Кирхгофа целесообразно проводить в следующем порядке.
На схеме электрической цепи обозначены узлы: 1 и 2. Обозначим на схеме токи в ветвях и стрелками произвольно укажем их положительные направления. Выберем два независимых контура и стрелками покажем направление их обхода.
Пусть силы тока для каждой ветви соответственно
или
По второму закону Кирхгофа для выбранных независимых контуров I и II имеем:
Подставляя значения сопротивлений и ЭДС в уравнения, получаем следующую математическую модель (систему линейных уравнений):
Систему уравнений решаем методом Гаусса.
Переходим к эквивалентной системе уравнений:
Используя программы Excel, получаем:
Итак, получаем Замечание: в данной задаче численные значения силы тока могут принимать дробные значения и отрицательные значения. В ответ записываем значения по модулю и округленными до трех знаков после запятой.
Ответ: силы тока в каждой ветви соответственно равны
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
1. К концу шнура, перекинутого через блок, подвешены грузы
2. Через невесомый блок, укрепленный на ребре призмы, грани которой
3.
ПРИЛОЖЕНИЕ 1
Методическая карта 1
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.21 (0.006 с.) |




 ,
,  ,
, 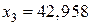 .
. ,
,  , но не удовлетворяет условию целочисленности.
, но не удовлетворяет условию целочисленности. ,
,  ,
,  .
.
 (см) отходов.
(см) отходов. ЭТАП: Исследование
ЭТАП: Исследование
 , где
, где  ,
,  ,
,  . А с условием целочисленности:
. А с условием целочисленности:  . Тогда для разрезания I способом нужно взять 56 прутков, II способом – 80 прутков, III – 62. Всего необходимо взять 56+80+62=198 прутков. При этом получим
. Тогда для разрезания I способом нужно взять 56 прутков, II способом – 80 прутков, III – 62. Всего необходимо взять 56+80+62=198 прутков. При этом получим  (см) отходов.
(см) отходов. . В результате получим несколько иной ответ.
. В результате получим несколько иной ответ. (см) отходов.
(см) отходов.
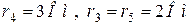 . Требуется определить токи в ветвях.
. Требуется определить токи в ветвях.
 ЭТАП: Подготовительный
ЭТАП: Подготовительный
 и число ветвей
и число ветвей  в электрической цепи. В соответствие с этим найти количество уравнений, которые необходимо составить по первому и второму законам Кирхгофа.
в электрической цепи. В соответствие с этим найти количество уравнений, которые необходимо составить по первому и второму законам Кирхгофа. уравнение по первому закону Кирхгофа. При этом считать положительными токи, входящие в узел, а отрицательными – выходящие из узла, или наоборот.
уравнение по первому закону Кирхгофа. При этом считать положительными токи, входящие в узел, а отрицательными – выходящие из узла, или наоборот. уравнений по второму закону Кирхгофа. В этих уравнениях ЭДС берется со знаком «+», если направление ЭДС совпадает с направлением обхода контура. Падение напряжений на сопротивлениях в замкнутом контуре электрической цепи берется со знаком «+», если направление обхода контура совпадает с выбранным направлением тока, и со знаком «-», если не совпадает.
уравнений по второму закону Кирхгофа. В этих уравнениях ЭДС берется со знаком «+», если направление ЭДС совпадает с направлением обхода контура. Падение напряжений на сопротивлениях в замкнутом контуре электрической цепи берется со знаком «+», если направление обхода контура совпадает с выбранным направлением тока, и со знаком «-», если не совпадает.

 ЭТАП: Построение математической модели
ЭТАП: Построение математической модели ,
,  и
и  . Тогда по первому закону Кирхгофа (для узла 2) получаем
. Тогда по первому закону Кирхгофа (для узла 2) получаем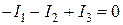 ,
,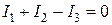 .
. ,
,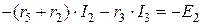 .
. Û
Û 
 ЭТАП: Решение математической задачи
ЭТАП: Решение математической задачи ~
~  ~
~  .
.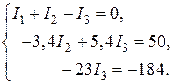 Û
Û 

 ЭТАП: Интерпретация решения математической задачи, исходя из условия прикладной задачи
ЭТАП: Интерпретация решения математической задачи, исходя из условия прикладной задачи ,
,  и
и 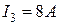 . Знак «-» в числовом значении
. Знак «-» в числовом значении  и
и  и
и  , причем
, причем  . Пренебрегая трением и считая шнур и блок невесомыми, а шнур нерастяжимым, определить ускорения, с которыми будут двигаться грузы, силу натяжения шнура и показания динамометра, на котором висит блок.
. Пренебрегая трением и считая шнур и блок невесомыми, а шнур нерастяжимым, определить ускорения, с которыми будут двигаться грузы, силу натяжения шнура и показания динамометра, на котором висит блок.



