
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема исследования и решения СЛУСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Найти ранги основной и расширенной матриц системы. Если 2. Если 3. Найти выражения базисных неизвестных через свободные. Полученные выражения являются общим решением системы. 4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения базисных неизвестных. Таким образом, можно найти частные решения исходной системы уравнений. Пример 5.6. Исследовать на совместность СЛУ. В случае совместности решить систему.
Решение. Составляем расширенную матрицу и преобразуем ее:
~
Исходная система свелась к ступенчатой:
Так как
Следовательно, неизвестные
Пусть
где , Если в примере 5.6. в общее решение вместо
5.4.Системы линейных однородных уравнений
Рассмотрим однородную систему линейных уравнений
Очевидно, что однородная система всегда совместна ( При каких условиях однородная система имеет и ненулевые решения?
Теорема 5.5. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных. Доказательство. Пусть Необходимость. Так как ранг Достаточность. Пусть , Теорема 5.6. Однородная система Данную теорему примем без доказательства.
Пример 5.7. Решить систему уравнений
Решение. Найдем ранг основной матрицы:
Пусть ,
ЗАДАНИЯ И ВОПРОСЫ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО РАЗДЕЛУ 1 «ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ»
МАТРИЦЫ
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Сформулировать определение матрицы. Как обозначаются элементы матрицы? 2. Какие матрицы называются равными? 3. Какие виды матриц Вы знаете? 4. Студенту дали задание, написать единичную матрицу 3-го порядка. Он сделал следующую запись: 5. Какие операции над матрицами называются линейными? Дайте им определения. 6. Сформулируйте свойства, которыми обладают линейные операции. 7. Какие матрицы называются согласованными? 8. Дайте определение произведения матриц 9. Сформулируйте свойства, которыми обладает произведение матриц. 10. Что называют целой положительной степенью квадратной матрицы 11. Дайте определение многочлена от матрицы 12. Какая матрица называется корнем многочлена 13. Устно проверьте, будет ли матрица
14. Какие преобразования являются элементарными? 15. Какие две матрицы 16. Какая матрица называется транспонированной относительно данной? 17. Студенту было дано задание: «Найти матрицу, транспонированную для матрицы
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 471; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.107 (0.011 с.) |

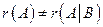 , то система несовместна.
, то система несовместна. , то система совместна. Найти какой-либо базисный минор порядка
, то система совместна. Найти какой-либо базисный минор порядка 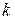 (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять
(напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять  неизвестных называют свободными и переносят в правые части уравнений.
неизвестных называют свободными и переносят в правые части уравнений.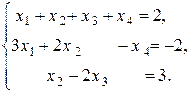
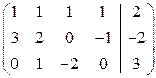 ~
~  ~
~  ~
~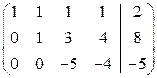
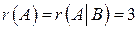 . Значит, система линейных уравнений совместна. Так как ранг матриц меньше числа неизвестных (
. Значит, система линейных уравнений совместна. Так как ранг матриц меньше числа неизвестных ( ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.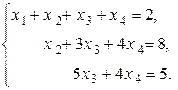
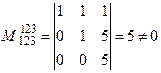 .
.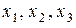 будут базисными, а неизвестная
будут базисными, а неизвестная  - свободной. Из последнего уравнения выражаем
- свободной. Из последнего уравнения выражаем 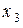 через
через 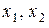 через
через 
 , где
, где  - любое действительное число. Тогда получаем общее решение системы
- любое действительное число. Тогда получаем общее решение системы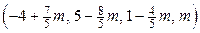 ,
,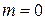 , то получаем частное решение
, то получаем частное решение 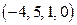 . Если подставить
. Если подставить 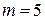 , то получаем частное решение
, то получаем частное решение 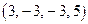 .
.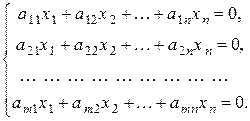
 ), она имеет нулевое (тривиальное) решение
), она имеет нулевое (тривиальное) решение 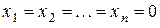 .
.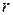 - ранг системы,
- ранг системы,  - число неизвестных.
- число неизвестных. . Пусть
. Пусть 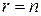 . Тогда один из миноров размера
. Тогда один из миноров размера 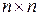 отличен от нуля. Поэтому система линейных уравнений имеет единственное решение:
отличен от нуля. Поэтому система линейных уравнений имеет единственное решение:  . Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то
. Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то  .
.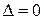 .
.
 ~
~  ~
~ 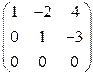 .
. , где
, где  - число неизвестных. Значит, система имеет бесчисленное множество решений. Так как
- число неизвестных. Значит, система имеет бесчисленное множество решений. Так как  , то неизвестные
, то неизвестные 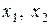 - базисные, а
- базисные, а 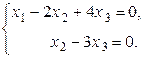 Û
Û 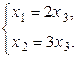
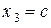 , где
, где 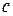 - любое действительное число. Тогда общее решение имеет вид:
- любое действительное число. Тогда общее решение имеет вид:  , где
, где 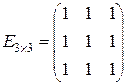 . Правильно ли он написал единичную матрицу? Ответ обоснуйте.
. Правильно ли он написал единичную матрицу? Ответ обоснуйте. и
и  .
. ?
? корнем многочлена
корнем многочлена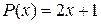 . Ответ обоснуйте.
. Ответ обоснуйте.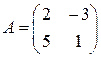 ». Он получил следующий ответ:
». Он получил следующий ответ: 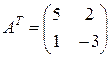 . Правильный ли результат? Ответ обоснуйте.
. Правильный ли результат? Ответ обоснуйте.


