
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составляем таблицу, рассматривая при этом три способы разрезания, которые обозначим произвольным образом.Содержание книги
Поиск на нашем сайте
- Что требуется найти в данной задаче? - Найти число разрезаемых прутков. - Сколько способов разрезания прутков? Как соотнести число разрезаемых прутков и число способов разрезания? - Рассматривается три способа разрезания. Значит, какая-то часть прутков будет разрезана по первому способу, какая-то часть – по второму и какая-то часть – по третьему способу. - Тогда, что можно взять за неизвестные?
Пусть
- Как связаны неизвестные с данными в таблице?
Так как число прутков для разрезания I способом равно Аналогично получаем уравнения по заготовкам вида
- В виде какого математического объекта запишем полученные связи? - В данной задаче получаем систему линейных уравнений. - Накладываются ли какие ограничения на неизвестные? - По смыслу задачи - Записать математическую модель исходной задачи.
Итак, математическая модель данной задачи имеет следующий вид:
при дополнительном условии:
- Сформулируйте математическую задачу. - Решить систему линейных уравнений.
- Какими методами можно решить математическую задачу? - Полученную систему линейных уравнений можно решить методом Гаусса, или по формулам Крамера, или матричным способом. - Решить систему линейных уравнений, выбранным Вами способом.
- Решите систему линейных уравнений с помощью компьютерной программы и проверьте полученные результаты.
Поскольку система линейных уравнений квадратная, то на компьютере воспользуемся матричным методом. Рассмотрим две матрицы:
Открываем экран Excel. Последовательно заносим в ячейки элементы матрицы В диалоговое окно Аргументы функции в ячейку Массив вносим B3:D5. В выделенной ячейке, например, B7 появляется надпись: =МОБР(B3:D5). Нажимаем ОК. В выделенной ячейке (в нашем случае это B7) появляется элемент первой строки и первого столбца обратной матрицы Выделяем диапазон (количество ячеек, как и у исходной матрицы, для которой находим обратную), начиная с той, в которой введена формула, например, B7:D9. Нажимаем клавишу F2. Затем нажимает клавиши Ctrl+Shift+Enter. В результате получаем обратную матрицу
На том же листе экрана Excel заносим в ячейки элементы матрицы В диалоговое окно Аргументы функции в ячейку Массив 1 вносим B7:D9, в ячейку Массив 2 вносим F3:F5. В выделенной ячейке, например, F7 появляется надпись: =МУМНОЖ(B7:D9; F3:F5). Нажимаем ОК. В выделенной ячейке (в нашем случае это F7) появляется элемент первой строки и первого столбца обратной матрицы
Как видим, результаты совпадают. Итак, решением системы линейных уравнений:
- Согласуется ли решение математической задачи условию прикладной задаче? - Так как Замечание: это значит, должны вернуться ко второму этапу, выбрать другие три способа разрезания прутков, заново составить и решить математическую модель. Опустим подробное поэтапное решение задачи.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.58 (0.006 с.) |

 - число прутков для разрезания I способом,
- число прутков для разрезания I способом,  - число прутков для разрезания II способом,
- число прутков для разрезания II способом,  - число прутков для разрезания III способом.
- число прутков для разрезания III способом. прутков вида
прутков вида  ; по II способу -
; по II способу -  и по III способу -
и по III способу -  . Всего заготовок вида
. Всего заготовок вида  или
или  .
. и
и  :
: ,
, .
. ,
,  ,
,  и
и  должны принимать целочисленные значения, т.е. значения, которые выражаются целым числом.
должны принимать целочисленные значения, т.е. значения, которые выражаются целым числом.
 , где
, где  .
. ЭТАП: Решение математической задачи
ЭТАП: Решение математической задачи Û
Û  Û
Û 
 и
и  .
. - Мастер функций. Выбираем категорию: математические функции. Из предложенных выбираем функцию МОБР (массив). Нажимаем ОК.
- Мастер функций. Выбираем категорию: математические функции. Из предложенных выбираем функцию МОБР (массив). Нажимаем ОК. .
.



 . Выделяем диапазон (количество ячеек, как у матрицы
. Выделяем диапазон (количество ячеек, как у матрицы  .
.

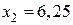 ,
,  .
. ЭТАП: Интерпретация решения математической задачи, исходя из условия прикладной задачи
ЭТАП: Интерпретация решения математической задачи, исходя из условия прикладной задачи , а по дополнительному условию
, а по дополнительному условию  ,
, 


