
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы нахождения обратной матрицыСодержание книги
Поиск на нашем сайте
1) Метод присоединенной матрицы. Из выше изложенного вытекает следующий алгоритм построения обратной матрицы методом присоединенной матрицы. 1. Вычислить определитель 2. Если 3. По формуле (3.2) составляем матрицу
2) Метод с использованием элементарных преобразований матриц. Матрица записывается в виде
3) Использование программы Excel пакета Microsoft Office. Для вычисления определителя из математических функций используется МОБР (массив).
Пример 3.3. Найти матрицу, обратную матрице A двумя способами, если
Решение. 1) Найдем матрицу, обратную данной, используя метод присоединенной матрицы. Находим определитель матрицы A.
Находим алгебраические дополнения каждого элемента матрицы A.
По аналогии находим остальные алгебраические дополнения:
Получаем обратную матрицу
2) Найдем матрицу, обратную данной, используя элементарные преобразования матрицы.
[умножаем первую строку на (-2) и складываем со второй строкой, складываем первую и третью строки]
[умножаем вторую строку на (-2) и складываем с третьей строкой]
[делим вторую строку на (-2) а третьей строкой - на 7]
[умножаем третью строку на складываем третью и первую строки]
[умножаем вторую строку на (-1) и складываем с первой строкой]
Итак,
3) Открываем экран Excel. Последовательно заносим в ячейки элементы матрицы в виде массива. Например, ячейки B3:D5. Входим в диалоговое окно
Рис. 1. Диалоговое окно Мастер функций В диалоговое окно Аргументы функции в ячейку Массив вносим B3:D5. В выделенной ячейке, например, B7 появляется надпись: =МОБР(B3:D5) (рис. 2). Нажимаем ОК. В выделенной ячейке (в нашем случае это B7) появляется элемент первой строки и первого столбца обратной матрицы.
Рис. 2. Диалоговое окно Аргументы функции Выделяем диапазон (количество ячеек, как и у исходной матрицы, для которой находим обратную), начиная с той, в которой введена формула, например, B7:D9. Нажимаем клавишу F2. Затем нажимает клавиши Ctrl+Shift+Enter. В результате получаем обратную матрицу (Рис. 3).
Рис. 3. Обратная матрица Замечание. Компьютер вычисляет значения элементов обратной матрицы до 16 знаков после запятой. В данном примере получили значения с 5-6 знаками после запятой, что поместилось в ячейках. ,
4. РАНГ МАТРИЦЫ
4.1. Определение. Свойства ранга матрицы
Рассмотрим матрицу A размера m ´ n
Выделим в ней k строк и k столбцов Определение 4.1. Минором k-го порядка матрицы A называется определитель, образованный элементами, стоящими на пересечении произвольно выбранных k строк и k столбцов. Обозначается минор k -го порядка матрицы A следующим образом: Например, рассмотрим матрицу
Миноры
Определение 4.2. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается Очевидно, что
Определение 4.3. Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Пример 4.1. Найти ранг матрицы:
Решение. Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля – это , Отметим свойства ранга матрицы: 1. При транспонировании матрицы ее ранг не меняется. 2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменяется. 3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.240 (0.005 с.) |

 . Если
. Если  , то
, то  не существует.
не существует.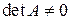 , то составляем присоединенную матрицу из алгебраических дополнений соответствующих элементов матрицы A.
, то составляем присоединенную матрицу из алгебраических дополнений соответствующих элементов матрицы A.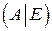 , где за вертикальной чертой приписывается единичная матрица того же порядка, как и матрица A. После использования элементарных преобразований получаем матрицу вида
, где за вертикальной чертой приписывается единичная матрица того же порядка, как и матрица A. После использования элементарных преобразований получаем матрицу вида  , т.е.
, т.е. .
. .
.

 .
. .
.

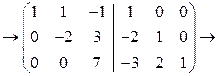

 и складываем со второй строкой,
и складываем со второй строкой,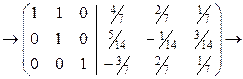

 .
. - Мастер функций. Выбираем категорию: математические функции. Из предложенных выбираем функцию МОБР (массив). Нажимаем ОК (Рис. 1).
- Мастер функций. Выбираем категорию: математические функции. Из предложенных выбираем функцию МОБР (массив). Нажимаем ОК (Рис. 1).


 .
. . Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы.
. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы. , где
, где  - номера выбранных строк,
- номера выбранных строк,  - номера выбранных столбцов.
- номера выбранных столбцов. .
.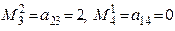 - есть миноры 1-го порядка; миноры
- есть миноры 1-го порядка; миноры 
 - есть миноры 2-го порядка,
- есть миноры 2-го порядка,  - минор 3-го порядка.
- минор 3-го порядка.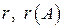 или
или  .
. , где
, где  - меньшее из чисел m и n.
- меньшее из чисел m и n. .
. . Значит,
. Значит,  . Все остальные миноры 2-го порядка равны нулю, поэтому минор
. Все остальные миноры 2-го порядка равны нулю, поэтому минор  является базисным.
является базисным.


