Механические силы в магнитном поле.
Из опыта известно, что на проводник с током в магнитном поле действует электромагнитная сила  Направление может быть установлено «правилом левой руки», а также введением понятия «бокового распора» магнитных линий, введенным В.Ф. Миткевичем. Направление может быть установлено «правилом левой руки», а также введением понятия «бокового распора» магнитных линий, введенным В.Ф. Миткевичем.
Механическое взаимодействие двух проводов с токами.
Как следует из рисунка, на 2-й провод действует сила  , F2 = B1 l I2 = ma H1 l I2 = ma , F2 = B1 l I2 = ma H1 l I2 = ma  . На первый провод: F1= ma . На первый провод: F1= ma  , т.е. F1 = F2. Сила, действующая на единицу длины провода: F0= ma , т.е. F1 = F2. Сила, действующая на единицу длины провода: F0= ma 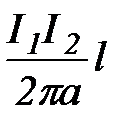 . Приближенно для воздушной среды: . Приближенно для воздушной среды:  [Н/м]. [Н/м].
Энергия магнитного поля. Распределение энергии
Энергия магнитного поля распределяется во всем объеме поля. При этом каждая точка поля характеризуется объемной плотностью энергии магнитного поля 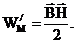 (3.15). Энергия магнитного поля в некотором объеме V (с учетом выражения (3.15)) равна: (3.15). Энергия магнитного поля в некотором объеме V (с учетом выражения (3.15)) равна: 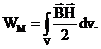 . Энергия магнитного поля системы n контуров с токами равна полусумме произведений токов в контурах на потокосцепление контуров . Энергия магнитного поля системы n контуров с токами равна полусумме произведений токов в контурах на потокосцепление контуров  . Так, энергия магнитного поля одного контура или катушки с током определяется (с учетом выражения (3.14)) следующим образом: . Так, энергия магнитного поля одного контура или катушки с током определяется (с учетом выражения (3.14)) следующим образом:  . Энергия системы двух контуров, связанных друг с другом посредством магнитного поля, равна: . Энергия системы двух контуров, связанных друг с другом посредством магнитного поля, равна: 
Синусоидальный ток в активном сопротивлении. Индуктивность в цепи синусоидального тока. Конденсатор в цепи синусоидального тока.
Резистор
Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напря  жение жение 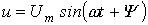 (см. рис. 1), то ток i через него будет равен (см. рис. 1), то ток i через него будет равен  (1) (1)
Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.
Из (1) вытекает:  ; ;  . .
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
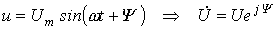 ; ;  , - разделим первый из них на второй: , - разделим первый из них на второй:  . Или . Или 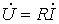 (2) (2)
Полученный результат показывает, что отношение двух комплексов есть вещественная константа.  Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.
Конденсатор
Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение 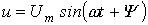 (см. рис. 4), то ток i через него будет равен (см. рис. 4), то ток i через него будет равен  (3) (3)
 Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на 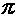 /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5. /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.
Из (3) вытекает:  ; ;  . .
Введенный параметр  называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление,  имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при  конденсатор представляет разрыв для тока, а при конденсатор представляет разрыв для тока, а при 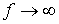  . .
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
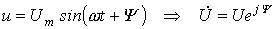 ; ;  , ,
- разделим первый из них на второй: 
 Или Или 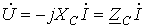 (4) (4)
В последнем соотношении  - комплексное сопротивление конденсатора. Умножение на - комплексное сопротивление конденсатора. Умножение на  соответствует повороту вектора на угол соответствует повороту вектора на угол 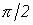 по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7. по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.
Катушка индуктивности
Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис. 8) определяется выражением  . Тогда для напряжения на зажимах катушки индуктивности можно записать . Тогда для напряжения на зажимах катушки индуктивности можно записать
  (5) (5)
Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на 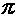 /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9. /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9.
 Из (5) вытекает: Из (5) вытекает:   . Введенный параметр . Введенный параметр  называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при  катушка индуктивности не оказывает сопротивления протекающему через него току, и при катушка индуктивности не оказывает сопротивления протекающему через него току, и при 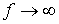  . .
Переходя от синусоидальных функций напряжения и тока к соответствующим комплексам:
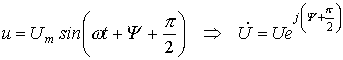 ; ; 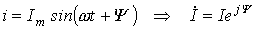 , разделим первый из них на второй: , разделим первый из них на второй:
  или или  (6) (6)
В полученном соотношении  - комплексное - комплексное
сопротивление катушки индуктивности. Умножение на  соответствует повороту вектора на угол соответствует повороту вектора на угол 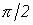 против часовой стрелки. Следовательно, уравнению (6) соответствует векторная диаграмма, представленная на рис. 11 против часовой стрелки. Следовательно, уравнению (6) соответствует векторная диаграмма, представленная на рис. 11
|