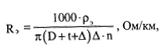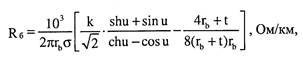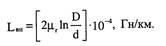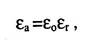Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет скорости распространения энергииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(1.72) Для определения скорости в определенных частотных областях следует пользоваться упрощенными формулами. В спектре низких частот (r=800 Гц):
(1.73) В области высоких частот (при w>40 кГц), когда скорость не зависит от частоты и определяется только параметрами кабеля:
(1.74) Для расчета скорости движения электромагнитной энергии постоянного тока можно использовать формулу:
(1.75) Скорость прохождения постоянного тока по линии составляет примерно 10 000 км/с, а токи высоких частот движутся со скоростью до 200 000 км/с, приближаясь к скорости света (с=300 000 км/с). РЕШЕНИЕ ЗАДАЧ 8. Определить минимальное и максимальное значения волнового сопротивления электромагнитной волне, проходящей по симметричной паре кабеля МКСГ 4x4, если кабель работает с системой передачи К-60. Решение. Максимальным волновое сопротивление будет на нижних частотах передаваемого сигнала, а минимальным - на верхних частотах. Минимальной и максимальной частотой передаваемого сигнала в аппаратуре К-60 будут соответственно 12 и 252 кГц. Для решения этой задачи воспользуемся формулами для расчета волнового сопротивления в различных частотных областях. Волновое сопротивление на частоте 12 кГц будет определяться по формуле (1.40), а на частоте 252 кГц -по формуле (1.11). Для расчетов по этим формулам нам необходимо сначала определить первичные параметры симметричной цепи - R, С, H, G на заданных частотах. Воспользуемся ранее представленной методикой расчета первичных параметров в задачах №4 - 7. Значение сопротивления на частоте 252 кГц было найдено в задаче №4. Определим R на частоте 12 кГц. Параметр кг составит для r=12 кГц:
Значения специальных функций Бесселя Р(кг), С(кг), Н(кг) находим из табл. 1.5: Р(кг)=0,0217; С(кг)=0,0583; Н(кг)=0,0842. Значение потерь Ответ: Максимальное волновое сопротивление 2=199,9е° Ом (на кГц); минимальное волновое сопротивление =,09 Ом (на 252 кГц). 9. Определить коэффициент затухания симметричной цепи в кабеле МКСГ 4x4, если кабель работает с системой передачи К-300. Показать, во сколько раз потери в металле больше или меньше потерь в диэлектрике. Расчеты проводить на верхней и нижней частоте системы передачи. Решение. Нижней и верхней частоте передаваемого сигнала в аппаратуре К-300 соответствует 60 и 1300 кГц. Для дальнейших расчетов воспользуемся формулой (1.12) Первый член в этих выражениях учитывает потери в металле, а второй - в диэлектрике. Соответственно потери в диэлектрике будут меньше на частоте 60 кГц в 487,3 раза, а на частоте 1300 кГц - меньше уже в 14,3 раза. Ответ: a=1,44 дБ/км; а20=6,86 дБ/км. Потери в диэлектрике на частоте 60 кГц будут меньше в 487,3 раза, а на частоте 1300 кГц -меньше в 14,3 раза.
РАСЧЕТ ВЗАИМНОГО ВЛИЯНИЯ В СИММЕТРИЧНЫХ ЦЕПЯХ ВОЗДУШНЫХ И КАБЕЛЬНЫХ ЛИНИЙ СВЯЗИ МЕТОДИЧЕСКИЕ УКАЗАНИЯ Воздушные линии В симметричных цепях, как в воздушных, так и в кабельных линиях, переходное влияние обусловлено электрическими и магнитными связями между цепями, которые выражаются результирующими электромагнитными связями на ближнем конце N12 и дальнем конце Р12: Для воздушных линий связи (ВЛС) формулы переходного затухания (рис. 1.6) принимают вид:
(1.78) (1.79) (1.80)
где R12 - электрическая связь, См/км; M12 - магнитная связь, Ом/км; 20lg волновое сопротивление симметричной цепи, Ом; h - активная составляющая электрической связи, См/км; r12 — емкостная связь, Ф/км; D - активная составляющая магнитной связи, Ом/км; l - индуктивная связь, Гн/км; w- круговая частота (со = 2711). в диэлектрике (s=0). Влияние учитывается лишь реактивными связями R12 и M12 Значения первичных параметров влияния r12 и D в воздушных линиях связи зависят в основном от взаимного расположения влияющих и подверженных влиянию цепей. Они могут быть рассчитаны по следующим выражениям:
(1.81) (1.82) где а - расстояние между проводами цепи; г - радиус провода; an - расстояние между первым проводом влияющей цепи и первым проводом цепи, подверженной влиянию (рис. 1.8); a24 - расстояние между вторым проводом влияющей цепи и вторым проводом цепи, подверженной влиянию; a21 расстояние между вторым проводом влияющей цепи и первым проводом цепи, подверженной влиянию; а14 - расстояние между первым проводом влияющей цепи и вторым проводом цепи, подверженной влиянию.
Рис. 1.8. К расчету электромагнитных связей в воздушных линиях связи а - коэффициент затухания; P- коэффициент фазы.
Рис. 1.6. Влияние между цепями
Рис. 1.7. К определению защищенности цепей: а) схема влияния; б) уровни в цепи 2 В результате того, что в воздушных линиях не учитываются активные составляющие связей, результирующие электромагнитные связи на ближнем и дальнем конце принимают значения:
(1.83)(1.84) При работе систем передачи В-12-2 и В-3-3 по воздушным линиям с медными или биметаллическими цепями, расстояние между усилительными пунктами составляет 250 км, а для систем передачи В-2-2 и В-3-3, работающих по ВЛС со стальными цепями, расстояние между усилительными пунктами составляет от 30 до 40 км.
(1.85) Защищенность на усилительный участок воздушной линии определяется выражением:
(1.86) где N - число усилительных участков. Переходное затухание на ближнем конце усилительного участка будет равно:
(1.87) где р - коэффициент отражения (для высокочастотных систем передачи р=0.1). Переходное затухание на дальнем конце усилительного участка будет равно: В воздушных линиях связи провода расположены на больших расстояниях друг от друга, и у них нет изоляционных покрытий. В этом случае в первичных параметрах влияния можно пренебречь активными составляющими связей (s и г), так как асимметрия потерь мало сказывается на вихревые токи (г=0) и невелика асимметрия потерь
(1.88) где I - длина усилительного участка. При неизменной длине усилительного участка среднее значение переходного затухания на ближнем конце в зависимости от частоты плавно уменьшается и на высоких частотах приближается к асимптотическому значению:
(1.89) где С - емкость цепи, Ф/км; k12 - емкостная связь, Ф/км.
(1.90) Переходное затухание на ближнем конце между несмещенными цепями определяется выражением:
(1.91) Где N12 - волновое сопротивление цепи; С - емкость цепи. Эффективность скрещивания на ближний конец (от скрещивания цепей с шагом 6, Т<1) определяется выражением:
(1.92) где Ап - длина волны; У- коэффициент распространения электромагнитной волны; S - шаг скрещивания; п - число секций скрещивания. Симметричные кабели Для скрученных кабельных симметричных цепей принимается геометрический закон сложения влияний в отдельных строительных длинах кабеля. В этом случае формулы переходного затухания (рис. 1.6) принимают вид:
(1.93)(1.94)(1.95)
где а - коэффициент затухания цепи, дБ/км; I- длина линии, км. В области низких частот преобладает емкостная связь, а другими составляющими взаимного влияния можно пренебречь. В области высоких частот учитываются все четыре составляющие связей. При этом количественное соотношение активных и реактивных составляющих связей в среднем равно:
(1.96)(1.97)
(1.98)(1.99) где k12 - емкостная связь между основными цепями четверки; ее значение задается в технических условиях на строительную длину кабеля. Перерасчет на нестандартную строительную длину осуществляется перемножением значения k12 для стандартной строительной длины на коэффициент, где L - нестандартная длина, м, C -стандартная длина, м. Для строительных длин определение переходных затуханий и защищенности производится по формулам:
(1.100)(1.101)(1.102) где а - коэффициент затухания цепи, дБ/км. Параметры влияния на усилительных участках связаны с параметрами влияния на строительных длинах следующими соотношениями:
(1.103)(1.104)(1.105) где п - число строительных длин; l строительная длина кабеля, км; а - коэффициент затухания цепи, дБ/км. В симметричных кабельных цепях переходное затухание и защищенность снижаются с ростом частоты и длины линии. Поэтому расчет взаимных влияний в аналоговом режиме следует проводить на частотах, одной из которых является наивысшая частота используемого диапазона системы передачи, а в цифровом режиме - на частотах, одной из которых является полу тактовая частота системы передачи. Влияние через третью цепь определяется выражением:
(1.106) l - длина усилительного участка. Рассчитанные значения переходного затухания на наивысшей частоте в аналоговом режиме необходимо сравнить с нормами для строительной длины усилительного участка.
Требуемое значение переходного затухания между трактами ЦСП на длине РГУ двух кабельной магистрали [4] определяется из выражения:
(1.107)
В существующих справочниках дана норма защищенности цепей строительных длин кабеля A D частоты 0,25 Мгц. Требуемые нормы для другой частоты определяются выражениями:
(1.108)
(1.109) где A3(fx;lx) определяемая защищенность на требуемой частоте 5x и необходимой длине участка lx; A3(fx;lx) - известное значение защищенности на известной частоте w и известной длине lx Для двухкабельной системы при наличии 6 трактов К-бОп и 2 трактов ИКМ-120 частотная зависимость защищенности аппроксимируется выражением [4]:
(1.110)
(1.111) ПРИЛОЖЕНИЕ Задачи для самостоятельного решения К разделу "Расчет элементов конструкций симметричных кабелей" П-1. Определить сколько кг меди и свинца находится в строительной длине кабеля ТГ 10x2x0,5. П-2. Найти расстояние между центрами пары проводников, находящихся внутри четверки в кабеле с кордельно-бумажной изоляцией МКГ-4х4x1,2 и определить диаметр звездной группы. П-3. Найти расстояние между центрами пары проводников, находящихся внутри четверки в кабеле с балонно-полиэтиленовой изоляцией МКПГ-4х4x1,2 и определить диаметр звездной группы. П-4. Найти расстояние между центрами пары проводников, находящихся внутри четверки в кабеле со сплошной полиэтиленовой изоляцией МКПВ-1х4х1,2 и определить диаметр звездной группы. П-5. Найти расстояние между центрами пары проводников, находящихся внутри четверки в кабеле с пористо-полиэтиленовой изоляцией МKПП-1х4x1,2 и определить диаметр звездной группы. К разделу "Расчет первичных параметров симметричных цепей" П-6. Определить, на сколько изменится сопротивление симметричной цепи в кабеле МКГ-4х4, если в первом случае по ней организован один стандартный канал тональной частоты, во втором случае была использована система передачи КРР-30, в третьем случае К-60. Расчеты проводить на верхних П-7. Определить, на сколько изменится сопротивление симметричной цепи в кабеле МКСГ-4х4, если в первом случае кабель находится среде с температурой t=+20°С, во втором случае - в среде с температурой 1= -30°С. По симметричной цепи работает система передачи k-60 Расчеты проводить цепи воздушной линии связи, если в первом случае симметричная цепь находится в среде с температурой t=+30°С, во втором случае -в среде с температурой t=-30°С. По симметричной цепи из стальных проводов диаметром 0=4 мм работает система передачи В-3-3. Расчеты проводить на верхней и нижней частоте передаваемых сигналов. П-9. Определить, во сколько изменится внутренняя индуктивность симметричной цепи в кабеле МКГ-4х4, если в первом случае по ней организован один стандартный канал тональной частоты, а во втором случае была использована система передачи К-60. Чему будут при этом равны общие значения индуктивности данной симметричной цепи. Расчеты проводить на верхних частотах передаваемых сигналов. П-10. Определить, на сколько изменится индуктивность первой симметричной цепи профиля №3 в воздушной линии связи, если в первом случае на ней использованы стальные провода диаметром 0=4 мм, а во втором - медные провода того же диаметра. По симметричной цепи работает система передачи В-3-3. Расчеты проводить на верхней и нижней частоте передаваемых сигналов. П-11. Определить, на сколько отличается емкость идеальной симметричной цепи от реальной симметричной цепи, находящейся в кабеле МКГ-4х4, если параметры идеальной цепи и симметричной цепи кабеля МКГ совпадают. П-12. Определить, на сколько отличается емкость реальной симметричной цепи в кабеле МКСГ-4х4x1,2 от симметричной цепи, в проводниках которой оказалось по два корделя. П-13. Определить, во сколько раз изменится проводимость изоляции симметричной пары, если она в первом случае находится в кабеле МКГ 1x4, а во втором случае в МКПГ 1x4. На кабелях работает система передачи КАМА. Расчеты проводить на верхней и нижней частоте системы передачи. К разделу "Расчет вторичных параметров симметричных цепей" П-14. Определить минимальное и максимальное значение волнового сопротивления электромагнитной волне, проходящей по симметричной паре кабеля ТПП 10x2x0,5. П-15. Определить значение волнового сопротивления электромагнитной волне, проходящей по симметричной паре кабеля МКГ-1х4. Расчеты проводить для постоянного тока. П-16. Определить коэффициент затухания симметричной цепи в кабеле МКГ-4х4, если кабель работает с системой передачи К-60. Расчеты проводить на нижней частоте системы передачи. П-17. Определить, на сколько изменится коэффициент затухания симметричной цепи в кабеле МКСГ-4х4, если в первом случае кабель находится в среде с температурой t=+20°С, во втором случае - в среде с температурой t= -30°С. По симметричной цепи работает система передачи К-60. Расчеты проводить на верхней и нижней частоте передаваемых сигналов. П-18. Определить коэффициент фазы симметричной цепи в кабеле МКГ-4х4, если кабель работает с системой передачи К-60. Расчеты проводить на нижней частоте системы передачи. П-19. Определить, на сколько отличается скорость движения низкочастотной составляющей сигнала по симметричной цепи в кабеле МКСГ-4х4 от скорости движения низкочастотной составляющей сигнала по симметричной цепи в кабеле МКГ-4х4, если кабели работают с системой передачи К-60. К разделу "Расчет взаимного влияния в симметричных цепях воздушных и кабельных линий связи" П-20. Определить электромагнитные связи первой и восьмой цепи на воздушной линии с профилем №4. Диаметр стальных проводов 0=4 мм. По воздушной линии работает система передач B-3-3. Расчеты проводить на верхней частоте системы передачи.
ГЛАВА 2 КОАКСИАЛЬНЫЕ КАБЕЛИ СВЯЗИ 2.1. ОСНОВНЫЕ ФОРМУЛЫ Оптимальное соотношение между диаметрами проводников коаксиальной пары:
(2.1) где D - диаметр внешнего проводника коаксиальной пары, мм; d - диаметр внутреннего проводника коаксиальной пары, мм; Qa - проводимость металла внешнего проводника; Qb - проводимость металла внутреннего проводника. Эквивалентное значение относительной диэлектрической проницаемости для шайбовой изоляции коаксиальной пары:
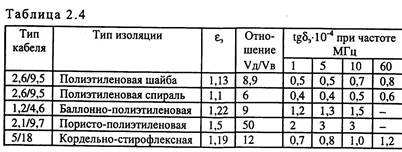
(2.2) где а - толщина шайбы, мм; Ь - расстояние между шайбами, мм; E - относительная диэлектрическая проницаемость воздуха; E - относительная диэлектрическая проницаемость материала шайбы. Эквивалентное значение тангенса угла диэлектрических потерь для шайбовой изоляции коаксиальной пары:
(2.3) где tg тангенс угла диэлектрических потерь материала шайбы. tg тангенс угла диэлектрических потерь воздуха. Активное сопротивление коаксиальной пары:
(2.4)
Ra - сопротивление внутреннего проводника, Ом/км; Rb- сопротивление внешнего проводника, Ом/км; d - диаметр внутреннего проводника, мм; D - диаметр внешнего проводника, мм; a- проводимость металла проводников; к - коэффициент вихревых токов;
(2.5) Сопротивление внутреннего проводника постоянному току:
(2.6)
d - диаметр голого проводника, мм; p - удельное сопротивление, Оммм2/м (табл.2.2). Сопротивление внешнего проводника, поверх которого наложено п стальных экранных лент:
(2.7)
Rm- сопротивление внешнего медного проводника, Ом/км; Ra- сопротивление экрана, Ом/км. Индуктивность коаксиальной цепи:
(2.8)
La — внутренняя индуктивность внутреннего проводнике, 1 н/км; Lb - внутренняя индуктивность внешнего проводника, Гн/км; Lbn - внешняя индуктивность цепи (или наружная межпроводниковая индуктивность), Гн/км. Емкость коаксиальной цепи:
(2.9) где Еа -абсолютная диэлектрическая проницаемость изоляции коаксиальной пары. Проводимость изоляции коаксиальной цепи:
(2.10) где w - круговая частота (w = 2пt) С - емкость коаксиальной цепи; tgb - тангенс угла диэлектрических потерь (табл. 2.4). Волновое сопротивление коаксиальной цепи:
(2.11) где L - индуктивность цепи, Гн/км; С - емкость цепи, Ф/км. Коэффициент затухания в коаксиальной цепи:
(2.12) где R - сопротивление цепи, Ом/км; С - проводимость изоляции цепи, См/км; L - индуктивность цепи, Гн/км; G - емкость цепи, Ф/км. Коэффициент фазы:
(2.13) Где w - круговая частота (со = 2gh) L - индуктивность цепи, Гн/км; С - емкость цепи, Ф/км. Скорость распространения энергии:
(2.14) Где L- индуктивность цепи, Гн/км; С - емкость цепи, Ф/км. Сопротивление связи:
(2.15) к - коэффициент вихревых токов (табл. 2.1); r - внутренний радиус внешнего проводника, мм; г - внешний радиус внешнего проводника, мм; А - толщина внешнего проводника, мм;
(2.16) где
L- сопротивление связи влияющей цепи; L - сопротивление связи цепи, подверженной влиянию; 2n - полное продольное сопротивление третьей цепи. Полное продольное сопротивление третьей цепи:
(2.17) где Z3 - собственное продольное сопротивление внешнего проводника влияющей цепи; Z11 - собственное продольное сопротивление внешнего проводника цепи, подверженной влиянию; wL3 - сопротивление третьей цепи, обусловленной внешней индуктивностью L3, создаваемой магнитным полем между внешними проводниками коаксиальных пар. Переходное затухание по мощности на ближнем конце при соприкасающихся внешних оголенных проводниках по всей длине:
(2.18) где 2b - волновое сопротивление коаксиальной цепи (2b=75 Ом); hj - коэффициент распространения электромагнитной энергии по коаксиальной цепи; L2 - полное продольное сопротивление третьей цепи; L - длина цепи влияния, км. Переходное затухание по мощности на дальнем конце при соприкасающихся внешних оголенных проводниках по всей длине:
(2.19) где а - коэффициент затухания цепи, дБ/км; A - защищенность от помех, дБ. Защищенность от помех при соприкасающихся внешних оголенных проводниках по всей длине:
(2.20) При коротких длинах и малых затуханиях коаксиальных цепей (низкие частоты) и при соприкасающихся внешних оголенных проводниках наблюдается равенство переходного затухания на ближнем конце и защищенности:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ Расчет сопротивления Коаксиальные кабели обычно используются в диапазоне частот свыше 60 кГц, при этом расчет первичных параметров на этих частотах можно производить по упрощенным формулам. Активное сопротивление коаксиальной пары состоит из сопротивления внутреннего проводника Ra и внешнего (полого) проводника Rb и рассчитывается Если внешний и внутренний проводники медные, то расчет следует проводить по формуле (2.5). Для коаксиальной пары из алюминиевых проводников формула (2.4) преобразуется в выражение:
(2.21) Если внутренний проводник коаксиальной пары медный, а внешний - алюминиевый, то активное сопротивление определяется из выражения:
(2.22) Электрическое сопротивление внутреннего проводника коаксиальной пары постоянному току определяется из выражения (2.6). Значение удельного сопротивления для различных металлов определяется из табл. 2.2.
Электрическое сопротивление внешнего проводника коаксиальной пары постоянному току определяется из выражения (2.7) как параллельное подключение сопротивления внешнего медного проводника Км и сопротивления экрана Rэ. Значение сопротивления постоянному току внешнего медного проводника определяется из выражения:
(2.23) Где Рm - удельное сопротивление меди, Омм /м (табл. 2.2); l - толщина ленты внешнего медного проводника, мм, o - внутренний диаметр внешнего проводника, мм. Значение сопротивления постоянному току экрана коаксиальной пары определяется из выражения:
(2.24) где рa - удельное сопротивление металла экранных лент, Ом-мм2/м (табл. 2.2); А- толщина экранных лент, мм; п - число экранных лент. При расчете активного сопротивления коаксиальной пары на частотах < 60 кГц расчеты следует производить по полным формулам. Сопротивление внутреннего проводника Ra в этом случае определяется из выражения:
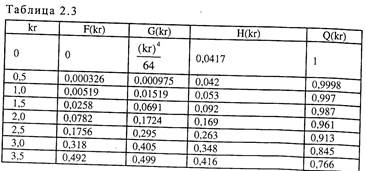
(2.25) где Ro - электрическое сопротивление внутреннего проводника коаксиальной пары постоянному току; Р (кг) - специальная функция, полученная с использованием видоизмененных функций Бесселя (табл. 2.3); Как видно из выражения для определения сопротивления цепи, необходимо сначала найти специальную функцию Бесселя Р (кг). Ее значение представлено в табл. 2.3. Аргументом этой функции является произведение коэффициента вихревых токов (табл. 2.1) на радиус голого проводника кг. Значения к даны в табл. 2.1.
Активное сопротивление внешнего проводника KS коаксиальной пары на частотах < 60 кГц определяется по формуле:
(2.26) где I - толщина внешнего проводника, мм; Гd - внутренний радиус внешнего проводника, мм; а - проводимость металла (табл. 2.1); к - коэффициент вихревых токов;
(2.31) Значение (кг) и аргумент функции кг определяются по аналогии с другой специальной функцией Бесселя р (кг) 0 из табл. 2.1 и 2.3. Методика нахождения этого параметра рассмотрен при расчете сопротивления коаксиальных пар где г - внутренний радиус внешнего проводника, мми; а - проводимость металла (табл. 2.1); со - круговая частота (со=2); к - коэффициент вихревых токов;
(2.34) Внутренняя индуктивность по абсолютной величине значительно меньше наружной и с ростом частоты ее относительное значение существенно снижается. Расчет емкости Емкость коаксиальной пары аналогична емкости цилиндрического конденсатора. Его электрическое поле создается между двумя цилиндрическими поверхностями с общей осью. Емкость определяется по формуле (2.9). В ряде случаев вместо данного выражения, в которое входит абсолютная диэлектрическая проницаемость изоляции коаксиальной пары, удобнее использовать формулу:
(2.35) где ек- относительная диэлектрическая проницаемость. Абсолютная диэлектрическая проницаемость среды – еа связана с относительной диэлектрической проницаемостью среды – ер выражением:
(2.36) где е0 - электрическая постоянная, равная (в системе СИ) 109/(3л;) Ф/м. Относительная диэлектрическая проницаемость всех материальных тел больше 1, или, другими словами, всякая материальная среда, уменьшает напряженность электрического поля, созданного зарядом, по сравнению с полем в пустоте. В ряде случаев возникает необходимость в расчете эквивалентной относительной диэлектрической проницаемости изоляции, особенно при различных соотношениях твердого диэлектрика и воздуха. Ее величина будет определяться из выражения: S1 и S2 - относительные диэлектрические проницаемости соответственно первого и второго диэлектриков; g и Z площади поперечного сечения первого и второго диэлектрика. Эквивалентное значение диэлектрической проницаемости для шайбовой изоляции коаксиальной пары определяется выражением (2.3). Коаксиальные кабели, как правило, имеют сложную комбинированную изоляцию. Результирующие эквивалентные значения относительной диэлектрической проницаемости S при таких комбинированных изоляциях приведены в табл. 2.4.
Расчет проводимости Проводимость изоляции О характеризует потери энергии в изоляции проводников коаксиальной пары. Проводимость изоляции обусловлена сопротивлением изоляции изолирующего материала и диэлектрическими потерями. Проводимость за счет диэлектрических потерь определяется из выражения (2.10). Проводимость, обусловленная утечкой тока в силу несовершенства изоляции, определяется из выражения С0=1R. Величина проводимости изоляции обратно пропорциональна сопротивлению изоляции кабеля. В коаксиальных кабелях R для коаксиальных пар среднего типа нормируется величиной 10 000 МОмкм. В результате проводимость изоляции коаксиального кабеля определяется из выражения:
(2.38) В используемом диапазоне частот (>60 кГц) первым членом можно пренебречь. Проводимость изоляции с ростом частоты линейно возрастает и ее величина зависит от качества диэлектрика, характеризуемого величиной угла диэлектрических потерь. По аналогии с нахождением эквивалентной диэлектрической проницаемости в ряде случаев возникает необходимость в расчете эквивалентной величины S5. Его значение будет определяться из выражения:
(2.39) где S1 и S2 - относительные диэлектрические проницаемости соответственно первого и второго диэлектриков; S1 и 53- площади поперечного сечения первого и второго диэлектрика; ] tg и tg2 - тангенс угла диэлектрических потерь первого и второго диэлектрика. Результирующие эквивалентные значения тангенса диэлектрических потерь при комбинированных изоляциях приведены в табл. 2.4. РЕШЕНИЕ ЗАДАЧ 1. Сравнить расчетные данные сопротивления коаксиальной пары в кабеле КТ, полученные по полным и упрощенным формулам. На кабеле работает система передачи К-300. Расчеты проводить на нижней частоте передаваемых сигналов. Решение. Для решения этой задачи необходимо знать конструктивные параметры данной коаксиальной пары: диаметр и материал жил, толщину и материал экрана. Для определения этих параметров необходимо воспользоваться [1, 2], в которых даны характеристики кабеля МКТ-4. Из [1,2] находим, что диаметр внутреннего медного проводника равен 1, 2 мм; изоляция - воздушно-полиэтиленовая, баллонного типа; внешний проводник - медный с внутренним диаметром 4,6 мм и толщиной ОД мм; экран - из двух стальных лент толщиной по ОД мм; нижняя частота системы передачи К-300 равна 60 кГц.
Вначале определим сопротивление коаксиальной пары по упрощенной формуле (2.5). Активное сопротивление коаксиальной пары будет равно:
Для дальнейших расчетов по полным формулам определим сопротивление внутреннего проводника по постоянному току из формулы (2.6):
Нижняя частота системы передач К-300 составляют 60 кГц. Из табл. 2.1 определим значение кг: для r=60 кГц: кг=00105а7=0,0105 1,2 760000 =3,1. Значение специальной функции Бесселя Р(кг) находим из табл. 2.3. Ее значение составит 0,353. Определим активное сопротивление внутреннего проводника по полной формуле (2.25): Расчет активного сопротивления внешнего проводника по полной формуле проводится по уравнению (2.26). Из табл. 2.1 определим параметр Определим величину параметра и: Величина активного сопротивления внешнего проводника будет равна: Общая величина сопротивления коаксиальной пары, полученная по полным формулам, будет равна: Таким образом, сопротивление коаксиальной пары, полученное по упрощенной формуле, ниже на 10,21 Ом/км сопротивления, полученного по полным формулам. Ответ: DK=10,21 Ом/км. 2. При эксплуатации магистрали, использующей кабель МКТ, была изменена схема дистанционного питания, в результате чего напряжение постоянного тока было подключено к внутреннему и внешнему проводнику одной коаксиальной пары. Найти сопротивление новой цепи дистанционного питания. Решение. Для решения используем найденные в предыдущей задаче конструктивные параметры коаксиальной пары, а также сопротивление внутреннего проводника по постоянному току: Для оценки сопротивления постоянному току внешнего медного проводника используем выражение (2.23). Величину удельного сопротивления меди найдем в табл. 2.2: Величину сопротивления постоянному току экр
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 2458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.110.5 (0.011 с.) |

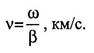 Скорость распространения электромагнитной энергии является функцией частоты и фазовой постоянной, которая в свою очередь зависит от первичных параметров линии. В общем виде она определяется по формуле:
Скорость распространения электромагнитной энергии является функцией частоты и фазовой постоянной, которая в свою очередь зависит от первичных параметров линии. В общем виде она определяется по формуле: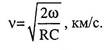









 Для снижения влияния между цепями необходимо уменьшить параметр:
Для снижения влияния между цепями необходимо уменьшить параметр:

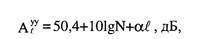

 Влияние от отражений на дальнем конце в воздушных линиях связи определяется в основном отражением от концов линий, значение которого оценивается переходным затуханием от отражений:
Влияние от отражений на дальнем конце в воздушных линиях связи определяется в основном отражением от концов линий, значение которого оценивается переходным затуханием от отражений:
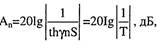

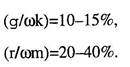



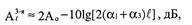


 где п - число трактов в кабеле; 10lg(n-1) значение полу тактовой частоты системы передачи.
где п - число трактов в кабеле; 10lg(n-1) значение полу тактовой частоты системы передачи. Норма защищенности цепей, оборудованных аппаратурой К-6Оп, от влияния цепей, оборудованных аппаратурой ИКМ-120, равна 52 дБ на регенерационный участок.
Норма защищенности цепей, оборудованных аппаратурой К-6Оп, от влияния цепей, оборудованных аппаратурой ИКМ-120, равна 52 дБ на регенерационный участок.






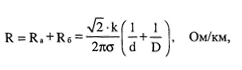

 где
где Активное сопротивление коаксиальной пары с медными проводниками:
Активное сопротивление коаксиальной пары с медными проводниками:



 где
где

 где
где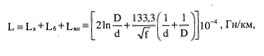


 где
где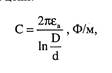
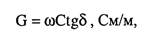

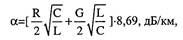

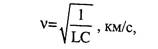








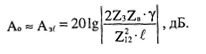 (2.20а)
(2.20а)


 2.2. РАСЧЕТ ПЕРВИЧНЫХ ПАРАМЕТРОВ КОАКСИАЛЬНЫХ ЦЕПЕЙ
2.2. РАСЧЕТ ПЕРВИЧНЫХ ПАРАМЕТРОВ КОАКСИАЛЬНЫХ ЦЕПЕЙ из выражения (2.4), где к - коэффициент вихревых токов определяется из выражения, где а - проводимость металла (табл. 2.1), - абсолютная магнитная проницаемость; | Гн/км -магнитная проницаемость вакуума, - относительная магнитная проницаемость для проводника (для медных проводников д =1, для алюминиевых =1, для стальных =130, для свинца =1). Значения к даны в табл. 2.1. Значения внутреннего и внешнего диаметра подставляются в мм, частота r* в Гц. Для стандартных габаритных соотношений медных проводников коаксиальной пары (1=3,6) около 80% сопротивления приходится на внутренний провод и 20% - на внешний.
из выражения (2.4), где к - коэффициент вихревых токов определяется из выражения, где а - проводимость металла (табл. 2.1), - абсолютная магнитная проницаемость; | Гн/км -магнитная проницаемость вакуума, - относительная магнитная проницаемость для проводника (для медных проводников д =1, для алюминиевых =1, для стальных =130, для свинца =1). Значения к даны в табл. 2.1. Значения внутреннего и внешнего диаметра подставляются в мм, частота r* в Гц. Для стандартных габаритных соотношений медных проводников коаксиальной пары (1=3,6) около 80% сопротивления приходится на внутренний провод и 20% - на внешний.