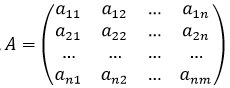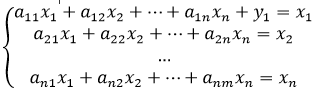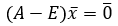Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная модель многоотраслевой экономикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для простоты будем полагать, что производственная сфера хозяйства представляет собой n отраслей, каждая из которых производит свой однородный продукт. Для обеспечения производства каждая отрасль нуждается в продукции других отраслей (производственное потребление). Обычно процесс производства рассматривается за некоторый период; в ряде случаев такой единицей служит год. Введем следующие обозначения: xi- общий объем продукции i-й отрасли; xij- объем продукции i-й отрасли, потребляемый j-й отраслью при производстве объема продукции xj; yi- объем продукции i-й отрасли, предназначенный для реализации (потребления) в непроизводственной сфере, или так называемый продукт конечного потребления. Балансовый принцип связи различных отраслей промышленности состоит в том, что валовой выпуск i-й отрасли должен быть равен сумме объемов потребления в производственной и непроизводственной сферах. В самой простой форме (гипотеза линейности, или простого сложения) балансовые соотношения имеет вид xi= xi1+xi2+xin, i=1, 2,..., n Эти уравнения называются соотношениями баланса. Поскольку продукция разных отраслей имеет разные измерения, в дальнейшем будем иметь в виду стоимостный баланс. В. Леонтьевым на основании анализа экономики США в период перед второй мировой войной был установлен важный факт: в течение длительного времени величины aij=xij/xj меняются очень незначительно и могут рассматриваться как постоянные числа. Это явление становится понятным в свете того, что технология производства остается на одном и том же уровне довольно длительное время, и, следовательно, объем потребления j-й отраслью продукции i-й отрасли при производстве своей продукции объема xj есть технологическая константа. В силу указанного факта можно сделать следующее допущение: для производства продукции j-й отрасли объема xj нужно использовать продукцию i-й отрасли объема aijxi, где aij - постоянное число. При таком допущении технология производства принимается линейной, а само это допущение называется гипотезой линейности. При этом числа aij называются коэффициентами прямых затрат. Согласно гипотезе линейности xij=aijxj, i,j=1, 2,..., n Соотношения баланса можно переписать в виде системы уравнений
Введем в рассмотрение векторы-столбцы объемов произведенной продукции (вектор валового выпуска), объемов продукции конечного потребления (вектор конечного потребления) и матрицу коэффициентов прямых затрат:
Тогда система уравнений в матричной форме имеет вид Уравнение межотраслевого баланса можно использовать в двух целях. В первом (наиболее простом) случае, когда известен вектор валового выпуска
Линейная модель торговли
Пусть аij - доля бюджета хj, которую j-я страна тратит на закупку товаров у i-й страны. Введем матрицу коэффициентов аij:
Тогда, если весь бюджет расходуется только на закупки внутри страны и вне ее (это можно трактовать как торговый бюджет), справедливо равенство
Матрица А с данным свойством, в силу которого сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли. Для i-й страны общая выручка от внутренней и внешней торговли выражается формулой Pi = ai1x1+ai2x2+…+ainxn Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е. xi ≤ Pi, или xi ≤ ai1x1+ai2x2+…+ainxn, i=1, 2, …, n. Докажем, что в условиях не может быть знака неравенства. Действительно, сложим все эти неравенства при i от 1 до n. Группируя слагаемые с величинами бюджетов xj, получаем: x1+x2+xn≤x1(a11+a21+...+an1)+x2(a12+a22+...+an2)+xn(a1n+a2n+...+anm) Нетрудно заметить, что в скобках стоят суммы элементов матрицы А по ее столбцам, которые равны единице по условию. Стало быть, мы получили неравенство x1+x2+...+xn≤x1+x2+...+xn, откуда следует, что возможен только знак равенства. Таким образом, условия принимают вид равенств:
ПОНЯТИЕ ФУНКЦИИ
Понятие функции в математике — одно из основных. Выражает зависимость одних переменных величин от других. Определение. Функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества. Пусть каждому числу x из множества значений D поставлено в соответствие число y из множества значений E. Чаще всего этот способ обозначают как y=f(x). Для обозначения функции применяют и другие буквы: y=g(x), s=f(t) и т.д. Если функция задана соответствием y=f(x), переменная x называется независимой переменной или аргументом, y — зависимой переменной или функцией. Множество значений D, которые может принимать x, называется областью определения функции. Множество значений E, которые может принимать y, называется областью значений функции. Функции, в которых значения аргумента и значения функции — числа, называются числовыми функциями. Примеры функций. 1) При движении автомобиля с постоянной скоростью пройденный путь является функцией от времени. 2) Периметр квадрата является функцией от его стороны. Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x), а f — функция от u: f=f(u), то функция y=f(u) — сложная. А u в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций. 1) y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, есл и u — некоторая функция от x. Примеры сложных функций с синусом: y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u. y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u. y=sin (x/7). Внутренняя функция u=x/7, внешняя функция f=sin u. 2) y=cos x — «простая» функция. y=cos u — сложная функция, если u — некоторая функция, зависящая от x. Примеры сложных функций с внешней функцией — косинусом: y=cos (4-11x). Внутренняя функция u=4-11x, внешняя функция — косинус: y=cos u. y=cos (7x³ -4x²). Внутренняя функция u=7x³ -4x², внешняя — y=cos u. Определение. Пусть дана функция y = f(x). Она имеет обратную, если из зависимости y = f(x) можно переменную x однозначно выразить через переменную y. Выразив x через y, мы получим равенство вида Дана функция y = f(x). Поставим следующий вопрос: при каком условии существует функция, обратная к функции f? Самым простым ответом на поставленный вопрос будет такой: по определению функция f имеет обратную, если из соотношения y = f(x) переменную x можно однозначно выразить через y. Условие существования обратной функции можно выразить геометрически. Функция y = f(x) имеет обратную, если всякая прямая y = y0 пересекает график функции y = f(x) не более чем в одной точке (она может совсем не пересекать график, если y0 не принадлежит области значений функции f). Если функция g является обратной для функции f, то и функция f является обратной для функции g, потому что равенства y = f(x) и x = g(y) по определению обратной функции равносильны, т. е. может существовать только одна пара чисел x и y, между которыми выполняется как зависимость y = f(x), так и зависимость x = g(y). В силу симметрии понятия обратной функции пару функций f и g называют взаимно обратными функциями.
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 788; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.28.200 (0.007 с.) |


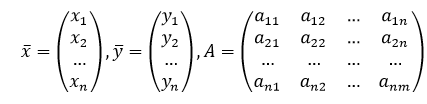

 , требуется рассчитать вектор конечного потребления
, требуется рассчитать вектор конечного потребления 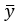 . Во втором случае уравнение межотраслевого баланса используется для целей планирования со следующей формулировкой задачи: для периода Т (например, год) известен вектор конечного потребления
. Во втором случае уравнение межотраслевого баланса используется для целей планирования со следующей формулировкой задачи: для периода Т (например, год) известен вектор конечного потребления