
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение методов линейной алгебры в экономикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математика и экономика-это самостоятельные области знаний, которые имеют свой объект и предмет исследования. Понятие матрицы и основанный на нем раздел математики, который называется, матричная алгебра, имеют большое значение для экономистов, основная часть математических моделей экономических объектов и процессов записывается в простой и компактной матричной форме. Производственные показатели Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в следующей таблице:
Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.
Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента
Расход сырья Предприятие выпускает четыре вида изделий с использованием четырех видов сырья. Нормы расхода сырья даны как элементы матрицы А:
Требуется найти затраты сырья каждого вида при заданном плане выпуска каждого вида изделия: соответственно, 60, 50, 35 и 40 ед. Решение: Составим вектор-план выпуска продукции:
Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду: этот вектор затрат вычисляется как произведение вектора
Конечный продукт отрасли Отрасль состоит из n предприятий, выпускающих по одному виду продукции каждое: обозначим объем продукции i-го предприятия через хi. Каждое из предприятий отрасли для обеспечения своего производства потребляет часть продукции, выпускаемой им самим и другими предприятиями. Пусть аij - доля продукции i-го предприятия, потребляемая j-м пред-приятием для обеспечения выпуска своей продукции объема хj. Найдем величину уi - количество продукции i-го предприятия, предназначенной для реализации вне данной отрасли (объем конечного продукта). Эта величина легко может быть подсчитана по формуле
Введем в рассмотрение квадратную матрицу порядка n, описывающую внутреннее потребление отрасли A=(aij), i, j = 1, 2,..., n Тогда вектор конечного продукта является решением матричного уравнения
с использованием единичной матрицы Е получаем
Пример. Пусть вектор выпуска продукции отрасли и матрица внутреннего потребления имеют, соответственно, вид
Получим вектор объемов конечного продукта, предназначенного для реализации вне отрасли, состоящей из трех предприятий:
Прогноз выпуска продукции Пусть C=(cij), i=1, 2,..., m, j=1, 2,..., n - матрица затрат сырья m видов при выпуске продукции n видов. Тогда при известных объемах запаса каждого вида сырья, которые образуют соответствующий вектор
Пример. Предприятие выпускает три вида продукции, используя сырье трех видов. Необходимые характеристики производства представлены следующими данными:
Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья. Задачи такого рода типичны при прогнозах и оценках функционирования предприятий, экспертных оценках проектов освоения месторождений полезных ископаемых, а также в планировании микроэкономики предприятий.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 2390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.120 (0.006 с.) |


 на три других вектора:
на три других вектора:






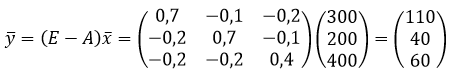
 , вектор-план
, вектор-план 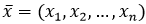 выпуска продукции определяется из решения системы m уравнений с n неизвестными:
выпуска продукции определяется из решения системы m уравнений с n неизвестными: где индекс "т" означает транспонирование вектора-строки в вектор-столбец.
где индекс "т" означает транспонирование вектора-строки в вектор-столбец.




