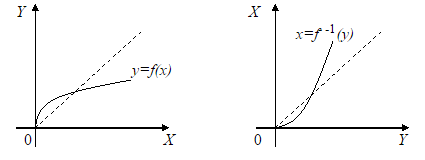Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение векторов и умножение на числоСтр 1 из 7Следующая ⇒
О КУРСЕ Современная математика интенсивно проникает в другие науки: во многом этот процесс происходит благодаря разделению математики на ряд самостоятельных областей. Язык математики универсален, что является объективным отражением универсальности законов окружающего нас многообразного мира.
ЦЕЛЬ: Основной целью курса является получение студентами теоретических знаний математического аппарата, необходимого для глубокого усвоения приложений математических методов к описанию современных экономических явлений и процессов. Задачи изучения дисциплины - получение базовых знаний по дисциплине, необходимые для понимания математических аспектов в экономических дисциплинах и решения практических задач в области экономики, использующих понятийный аппарат и методы математической экономики ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ: В процессе изучения курса “Математика в экономике” студенты должны:
ОСНОВНЫЕ ПОНЯТИЯ Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Длиной (или модулем) вектора называется расстояние между точками A и B. Модуль вектора обозначается символом Вектор, длина которого равна 1, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора Два вектора называются равными, если они коллинеарны, одинаковы направлены и имеют одинаковые длины. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любых коллинеарны, то такие векторы компланарны СМЕШАННОЕ ПРОИЗВЕДЕНИЕ Смешанным произведением векторов
Геометрический смысл смешанного произведения: смешанное произведение векторов 1. Условие компланарности векторов: три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
2. 3. 4.
СИСТЕМЫ КООРДИНАТ Декартова система координат определяется некоторой ее точкой O и базисом из двух векторов, параллельных плоскости. Точка O называется началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. Они лежат в плоскости и называются осями абсцисс и ординат. Каждая ось координат является числовой осью с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM (радиус–вектор точки М)
Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной. На плоскости часто употребляется также полярная система координат
Она определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Полярными координатами ρ и φ точки M называются расстояние ρ от полюса до точки M (ρ = |OM|) и угол φ между полярной осью и вектором OM. Угол φ называется полярным углом, измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Полярные координаты точки O: ρ = 0, угол φ не определен. У остальных точек ρ > 0 и угол φ определен с точностью до 2π. Обычно полагают 0 ≤ φ < 2π или − π < φ ≤ π. Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и φ формулами x = ρcosφ y = ρsinφ. Полярные координаты ρ и φ точки M выражаются через ее декартовы координаты x и y формулами:
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ В декартовой системе координат на плоскости каждая прямая определяется уравнением 1–й степени и, обратно, каждое уравнение 1–й степени определяет прямую. Уравнение вида Ax + By + Cz = 0 называется общим уравнением прямой. Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом (b — ордината точки пересечения прямой с осью OY). Угловым коэффициентом k прямой называется число k = tgα, где α — угол наклона прямой к оси OX (0 ≤ α < π). Уравнение прямой Уравнение прямой, проходящей через две точки M1(x1, y1) и M2(x2, y2), имеет вид Угол между прямыми с угловыми коэффициентами k1 и k2 определяется формулой: Условие параллельности прямых: k1 = k2 Условие перпендикулярности прямых: k1k2 = −1
МАТРИЦЫ Матрицей размера m×n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов: Числа aij (i = 1, …, m, j = 1, …, n) называются элементами матрицы A. Первый индекс обозначает номер строки, второй — номер столбца, в которых находится данный элемент.
Квадратная матрица, все элементы которой, стоящие на главной диагонали, равны единице, а остальные — нулю, т.е. матрица вида В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике. Матрицы A = (aij) и B = (bij) называются равными, если они одного и того же размера m×n и i = 1, …, m, j = 1, …, n aij = bij.
Транспонированная матрица обозначается символом AT.
Действия над матрицами Сложение матриц · A + B = B + A; · (A + B) + C = A + (B + C); · если O — нулевая матрица размера m×n, то A + O = A; A + (−A) = O. Умножение матрицы на число · 1•A = A; · α(βA) = (αβ)A. Для любых матриц A и B одного и того же размера и любых чисел α, β · (α + β)A = αA + βA; · α(A + B) = αA + αB. Операции сложения и умножения на число называют линейными операциями. Элементарные преобразования матриц Элементарными преобразованиями матриц являются:
· перестановка местами двух параллельных рядов матрицы; · умножение всех элементов ряда матрицы на число, отличное от нуля; · прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженные на одно и то же число. Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований.
· Умножение матриц ассоциативно, т.е. выполняется равенство (A•B)•C = A•(B• C) · Умножение матриц дистрибутивно по отношению к сложению, т.е. если определено выражение A•(B + C), то A•(B + C) = A•B + A •C.
ОПРЕДЕЛИТЕЛИ Пусть A = (aij) (i, j = 1, …, n) — квадратная матрица порядка n. Определитель матрицы n×n называется определителем n–го порядка.
вычисляется по правилу Саррюса: приписать к определителю справа два первых столбца, не меняя их порядка, и составить сумму произведений элементов главной диагонали и элементов, параллельных ей, из которой затем вычесть сумму произведений элементов побочной диагонали и элементов параллельных ей.
или Свойства определителей 1. При транспонировании матрицы величина ее определителя не меняется, т.е. 2. Отсюда следует, что любое утверждение, справедливое для столбцов определителя, справедливо также и для строк.
3. При перестановке двух столбцов (или строк) матрицы ее определитель меняет знак на противоположный.
РАНГ МАТРИЦЫ Основные понятия Свойства ранга матрицы
1. Если матрица А имеет размеры mxn, то rang A 2. rang A =0 тогда и только тогда, когда все элементы матрицы А равны 0; 3. Если матрица А - квадратная порядка n, то rang A = n тогда и только тогда, когда Элементарные преобразования 1. отбрасывание нулевой строки (столбца); 2. умножение всех элементов строки (столбца) матрицы на число, не равное нулю; 3. изменение порядка строк (столбцов) матрицы; 4. прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число; 5. транспонирование матрицы. С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
Метод окаймляющих миноров 1. Найти какой–либо минор М1 первого порядка (т.е. элемент матрицы), отличный от нуля. Если такого минора нет, то матрица А нулевая и r(A) = 0 2. Вычислять миноры 2-го порядка, содержащие М1 (окаймляющие М1) до тех пор, пока не найдется минор М2, отличный от нуля. Если такого минора нет, то r(A) = 1, если есть, то r(A) 3. Вычислять (если они существуют) миноры к-го порядка, окаймляющие минор Мк-1 При нахождении ранга матрицы таким способом достаточно на каждом шаге найти всего один ненулевой минор к-го порядка, причем искать его только среди миноров, содержащих минор Мк-1
ОБРАТНАЯ МАТРИЦА Матрица A − 1 называется обратной к квадратной матрице A n –го порядка, если A • A − 1 = A − 1 • A = E, где E — единичная матрица n –ого порядка. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е.det A ≠ о. Если det A=0, то матрица А называется вырожденной. Если обратная матрица существует, то она единственная. Вычисление обратной матрицы с помощью алгебраических дополнений
Матричные уравнения Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом: А*Х=В (1) Х*А=В (2) А*Х*С=В (3) В этих уравнениях А, В, С, Х - матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров. Если в уравнениях (1), (2) матрица А невырожденная, то их решения записываются следующим образом: Х=А-1*В, Х=В*А-1 Если в уравнении (3) матрицы А и С невырождены, то его решение записывается так: Х=А-1*В*С-1 Производственные показатели Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в следующей таблице:
Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.
Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента
Расход сырья Предприятие выпускает четыре вида изделий с использованием четырех видов сырья. Нормы расхода сырья даны как элементы матрицы А:
Требуется найти затраты сырья каждого вида при заданном плане выпуска каждого вида изделия: соответственно, 60, 50, 35 и 40 ед. Решение: Составим вектор-план выпуска продукции:
Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду: этот вектор затрат вычисляется как произведение вектора
Конечный продукт отрасли Отрасль состоит из n предприятий, выпускающих по одному виду продукции каждое: обозначим объем продукции i-го предприятия через хi. Каждое из предприятий отрасли для обеспечения своего производства потребляет часть продукции, выпускаемой им самим и другими предприятиями. Пусть аij - доля продукции i-го предприятия, потребляемая j-м пред-приятием для обеспечения выпуска своей продукции объема хj. Найдем величину уi - количество продукции i-го предприятия, предназначенной для реализации вне данной отрасли (объем конечного продукта). Эта величина легко может быть подсчитана по формуле
Введем в рассмотрение квадратную матрицу порядка n, описывающую внутреннее потребление отрасли A=(aij), i, j = 1, 2,..., n Тогда вектор конечного продукта является решением матричного уравнения
с использованием единичной матрицы Е получаем
Пример. Пусть вектор выпуска продукции отрасли и матрица внутреннего потребления имеют, соответственно, вид
Получим вектор объемов конечного продукта, предназначенного для реализации вне отрасли, состоящей из трех предприятий:
Прогноз выпуска продукции Пусть C=(cij), i=1, 2,..., m, j=1, 2,..., n - матрица затрат сырья m видов при выпуске продукции n видов. Тогда при известных объемах запаса каждого вида сырья, которые образуют соответствующий вектор
Пример. Предприятие выпускает три вида продукции, используя сырье трех видов. Необходимые характеристики производства представлены следующими данными:
Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья. Задачи такого рода типичны при прогнозах и оценках функционирования предприятий, экспертных оценках проектов освоения месторождений полезных ископаемых, а также в планировании микроэкономики предприятий. Линейная модель торговли
Пусть аij - доля бюджета хj, которую j-я страна тратит на закупку товаров у i-й страны. Введем матрицу коэффициентов аij:
Тогда, если весь бюджет расходуется только на закупки внутри страны и вне ее (это можно трактовать как торговый бюджет), справедливо равенство
Матрица А с данным свойством, в силу которого сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли. Для i-й страны общая выручка от внутренней и внешней торговли выражается формулой Pi = ai1x1+ai2x2+…+ainxn Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е. xi ≤ Pi, или xi ≤ ai1x1+ai2x2+…+ainxn, i=1, 2, …, n. Докажем, что в условиях не может быть знака неравенства. Действительно, сложим все эти неравенства при i от 1 до n. Группируя слагаемые с величинами бюджетов xj, получаем: x1+x2+xn≤x1(a11+a21+...+an1)+x2(a12+a22+...+an2)+xn(a1n+a2n+...+anm) Нетрудно заметить, что в скобках стоят суммы элементов матрицы А по ее столбцам, которые равны единице по условию. Стало быть, мы получили неравенство x1+x2+...+xn≤x1+x2+...+xn, откуда следует, что возможен только знак равенства. Таким образом, условия принимают вид равенств:
ПОНЯТИЕ ФУНКЦИИ
Понятие функции в математике — одно из основных. Выражает зависимость одних переменных величин от других. Определение. Функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества. Пусть каждому числу x из множества значений D поставлено в соответствие число y из множества значений E. Чаще всего этот способ обозначают как y=f(x). Для обозначения функции применяют и другие буквы: y=g(x), s=f(t) и т.д. Если функция задана соответствием y=f(x), переменная x называется независимой переменной или аргументом, y — зависимой переменной или функцией. Множество значений D, которые может принимать x, называется областью определения функции. Множество значений E, которые может принимать y, называется областью значений функции. Функции, в которых значения аргумента и значения функции — числа, называются числовыми функциями. Примеры функций. 1) При движении автомобиля с постоянной скоростью пройденный путь является функцией от времени. 2) Периметр квадрата является функцией от его стороны. Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x), а f — функция от u: f=f(u), то функция y=f(u) — сложная. А u в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций. 1) y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, есл и u — некоторая функция от x. Примеры сложных функций с синусом: y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u. y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u. y=sin (x/7). Внутренняя функция u=x/7, внешняя функция f=sin u. 2) y=cos x — «простая» функция. y=cos u — сложная функция, если u — некоторая функция, зависящая от x. Примеры сложных функций с внешней функцией — косинусом: y=cos (4-11x). Внутренняя функция u=4-11x, внешняя функция — косинус: y=cos u. y=cos (7x³ -4x²). Внутренняя функция u=7x³ -4x², внешняя — y=cos u. Определение. Пусть дана функция y = f(x). Она имеет обратную, если из зависимости y = f(x) можно переменную x однозначно выразить через переменную y. Выразив x через y, мы получим равенство вида Дана функция y = f(x). Поставим следующий вопрос: при каком условии существует функция, обратная к функции f? Самым простым ответом на поставленный вопрос будет такой: по определению функция f имеет обратную, если из соотношения y = f(x) переменную x можно однозначно выразить через y. Условие существования обратной функции можно выразить геометрически. Функция y = f(x) имеет обратную, если всякая прямая y = y0 пересекает график функции y = f(x) не более чем в одной точке (она может совсем не пересекать график, если y0 не принадлежит области значений функции f). Если функция g является обратной для функции f, то и функция f является обратной для функции g, потому что равенства y = f(x) и x = g(y) по определению обратной функции равносильны, т. е. может существовать только одна пара чисел x и y, между которыми выполняется как зависимость y = f(x), так и зависимость x = g(y). В силу симметрии понятия обратной функции пару функций f и g называют взаимно обратными функциями.
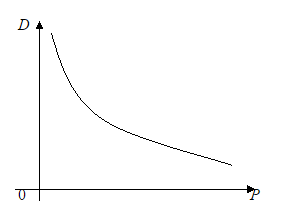
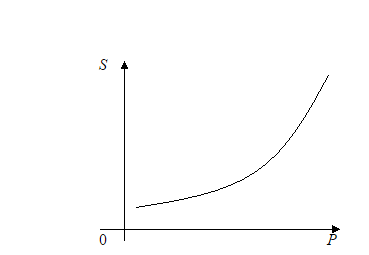
Производственные функции Рассмотрим некоторую производственную систему. Определение. Функция, выражающая зависимость объема производства от величины затраченных ресурсов, называется производственной. Существует целое семейство производственных функций. Рассмотрим производственную функцию y=f(x), где х – суммарная величина затрат в стоимостном выражении, у – суммарный выпуск в стоимостном выражении. По своему экономическому смыслу, х Если предположить, что производственная функция строго возрастает, т.е. любое увеличение затрат ведет к увеличению выпуска, то производственная функция имеет обратную функцию x=f-1(y), которая определяет величину производственных затрат х, необходимых для выпуска объема у. Эта функция называется функцией затрат. Она будет строго возрастающей. Кривые спроса и предложения. Точка равновесия D=kPa+c, где а < 0. Рассмотрим функцию предложения S от цены на товар P. Предложение растет с увеличением цены на товар. Зависимость S от Р имеет следующий вид: S=Pb+d, где b Параметры c и d - так называемые экзогенные величины; они зависят от ряда причин (благосостояние общества, политическая обстановка и т.п.). Переменные, входящие в формулы, положительны, поэтому графики функций имеют смысл только в первой координатной четверти. Для экономики представляет интерес условие равновесия, т.е. когда спрос равен предложению. Такое условие задается уравнением D(P)=S(P)
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.40.207 (0.17 с.) |
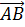 . Вектор
. Вектор 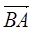 (у него начало в точке В, а конец в точке А) называется противоположным вектору
(у него начало в точке В, а конец в точке А) называется противоположным вектору 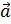 . Вектор, равный по длине вектору
. Вектор, равный по длине вектору 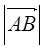 . Вектор нулевой длины называется нулевым и обозначается символом
. Вектор нулевой длины называется нулевым и обозначается символом 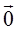 . Нулевой вектор направления не имеет.
. Нулевой вектор направления не имеет. называется число, обозначаемое
называется число, обозначаемое  и определяемое равенством
и определяемое равенством 
 умножается скалярно на третий вектор
умножается скалярно на третий вектор  .
.
 — правая, и со знаком «−», если тройка векторов — левая.
— правая, и со знаком «−», если тройка векторов — левая. 








 называется уравнением прямой в отрезках (a — абсцисса точки пересечения прямой с осью OX, b — ордината точки пересечения прямой с осью OY).
называется уравнением прямой в отрезках (a — абсцисса точки пересечения прямой с осью OX, b — ордината точки пересечения прямой с осью OY). .
.




 R:
R:





 разложение по i–ой строке
разложение по i–ой строке разложение по j–ому столбцу.
разложение по j–ому столбцу.
 min(m;n);
min(m;n); .
. где
где 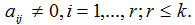
 не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:  , где 0 = (0,0,…,0). В противном случае строки матрицы называются линейно независимыми.
, где 0 = (0,0,…,0). В противном случае строки матрицы называются линейно независимыми. 2 и т.д.
2 и т.д. 0. Если таких миноров нет или они все равны нулю, то r(А) = k-1; если есть хотя бы один такой минор Мк
0. Если таких миноров нет или они все равны нулю, то r(А) = k-1; если есть хотя бы один такой минор Мк 




 на три других вектора:
на три других вектора:






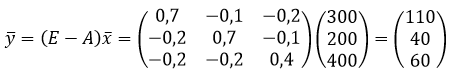
 , вектор-план
, вектор-план 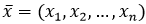 выпуска продукции определяется из решения системы m уравнений с n неизвестными:
выпуска продукции определяется из решения системы m уравнений с n неизвестными: где индекс "т" означает транспонирование вектора-строки в вектор-столбец.
где индекс "т" означает транспонирование вектора-строки в вектор-столбец.

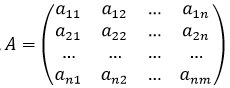

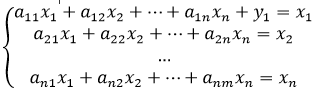
 , каждая компонента которого характеризует бюджет соответствующей страны. Тогда систему уравнений можно записать в матричной форме:
, каждая компонента которого характеризует бюджет соответствующей страны. Тогда систему уравнений можно записать в матричной форме: 
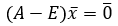
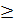 0 и у
0 и у