
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства линейных операций с векторамиСодержание книги
Поиск на нашем сайте
Для любых векторов 1. 2. 3. 4. 5. 6. 7.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Скалярным произведением векторов Свойства скалярного произведения векторов
Из определения скалярного произведения следует, что угол между ненулевыми векторами
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Векторным произведением векторов
3. Векторы
Замечание. Это определение однозначно определяет векторное произведение ненулевых векторов. Если хотя бы один из сомножителей — нулевой вектор, то векторное произведение считается равным нулевому вектору.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ Смешанным произведением векторов
Геометрический смысл смешанного произведения: смешанное произведение векторов 1. Условие компланарности векторов: три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю. 2. 3. 4.
СИСТЕМЫ КООРДИНАТ Декартова система координат определяется некоторой ее точкой O и базисом из двух векторов, параллельных плоскости. Точка O называется началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. Они лежат в плоскости и называются осями абсцисс и ординат. Каждая ось координат является числовой осью с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM (радиус–вектор точки М)
Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной. На плоскости часто употребляется также полярная система координат
Она определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Полярными координатами ρ и φ точки M называются расстояние ρ от полюса до точки M (ρ = |OM|) и угол φ между полярной осью и вектором OM. Угол φ называется полярным углом, измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Полярные координаты точки O: ρ = 0, угол φ не определен. У остальных точек ρ > 0 и угол φ определен с точностью до 2π. Обычно полагают 0 ≤ φ < 2π или − π < φ ≤ π. Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и φ формулами x = ρcosφ y = ρsinφ.
Полярные координаты ρ и φ точки M выражаются через ее декартовы координаты x и y формулами:
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ В декартовой системе координат на плоскости каждая прямая определяется уравнением 1–й степени и, обратно, каждое уравнение 1–й степени определяет прямую. Уравнение вида Ax + By + Cz = 0 называется общим уравнением прямой. Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом (b — ордината точки пересечения прямой с осью OY). Угловым коэффициентом k прямой называется число k = tgα, где α — угол наклона прямой к оси OX (0 ≤ α < π). Уравнение прямой Уравнение прямой, проходящей через две точки M1(x1, y1) и M2(x2, y2), имеет вид Угол между прямыми с угловыми коэффициентами k1 и k2 определяется формулой: Условие параллельности прямых: k1 = k2 Условие перпендикулярности прямых: k1k2 = −1
МАТРИЦЫ Матрицей размера m×n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов: Числа aij (i = 1, …, m, j = 1, …, n) называются элементами матрицы A. Первый индекс обозначает номер строки, второй — номер столбца, в которых находится данный элемент. Квадратная матрица, все элементы которой, стоящие на главной диагонали, равны единице, а остальные — нулю, т.е. матрица вида В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике. Матрицы A = (aij) и B = (bij) называются равными, если они одного и того же размера m×n и i = 1, …, m, j = 1, …, n aij = bij.
Транспонированная матрица обозначается символом AT.
Действия над матрицами Сложение матриц · A + B = B + A; · (A + B) + C = A + (B + C); · если O — нулевая матрица размера m×n, то A + O = A; A + (−A) = O. Умножение матрицы на число
· 1•A = A; · α(βA) = (αβ)A. Для любых матриц A и B одного и того же размера и любых чисел α, β · (α + β)A = αA + βA; · α(A + B) = αA + αB. Операции сложения и умножения на число называют линейными операциями. Элементарные преобразования матриц Элементарными преобразованиями матриц являются: · перестановка местами двух параллельных рядов матрицы; · умножение всех элементов ряда матрицы на число, отличное от нуля; · прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженные на одно и то же число. Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований.
· Умножение матриц ассоциативно, т.е. выполняется равенство (A•B)•C = A•(B• C) · Умножение матриц дистрибутивно по отношению к сложению, т.е. если определено выражение A•(B + C), то A•(B + C) = A•B + A •C.
ОПРЕДЕЛИТЕЛИ Пусть A = (aij) (i, j = 1, …, n) — квадратная матрица порядка n. Определитель матрицы n×n называется определителем n–го порядка.
вычисляется по правилу Саррюса: приписать к определителю справа два первых столбца, не меняя их порядка, и составить сумму произведений элементов главной диагонали и элементов, параллельных ей, из которой затем вычесть сумму произведений элементов побочной диагонали и элементов параллельных ей.
или Свойства определителей 1. При транспонировании матрицы величина ее определителя не меняется, т.е. 2. Отсюда следует, что любое утверждение, справедливое для столбцов определителя, справедливо также и для строк. 3. При перестановке двух столбцов (или строк) матрицы ее определитель меняет знак на противоположный.
РАНГ МАТРИЦЫ Основные понятия Свойства ранга матрицы
1. Если матрица А имеет размеры mxn, то rang A 2. rang A =0 тогда и только тогда, когда все элементы матрицы А равны 0; 3. Если матрица А - квадратная порядка n, то rang A = n тогда и только тогда, когда Элементарные преобразования 1. отбрасывание нулевой строки (столбца); 2. умножение всех элементов строки (столбца) матрицы на число, не равное нулю; 3. изменение порядка строк (столбцов) матрицы; 4. прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число; 5. транспонирование матрицы. С помощью элементарных преобразований матрицу можно привести к ступенчатому виду:
Метод окаймляющих миноров 1. Найти какой–либо минор М1 первого порядка (т.е. элемент матрицы), отличный от нуля. Если такого минора нет, то матрица А нулевая и r(A) = 0 2. Вычислять миноры 2-го порядка, содержащие М1 (окаймляющие М1) до тех пор, пока не найдется минор М2, отличный от нуля. Если такого минора нет, то r(A) = 1, если есть, то r(A)
3. Вычислять (если они существуют) миноры к-го порядка, окаймляющие минор Мк-1 При нахождении ранга матрицы таким способом достаточно на каждом шаге найти всего один ненулевой минор к-го порядка, причем искать его только среди миноров, содержащих минор Мк-1
ОБРАТНАЯ МАТРИЦА Матрица A − 1 называется обратной к квадратной матрице A n –го порядка, если A • A − 1 = A − 1 • A = E, где E — единичная матрица n –ого порядка. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е.det A ≠ о. Если det A=0, то матрица А называется вырожденной. Если обратная матрица существует, то она единственная. Вычисление обратной матрицы с помощью алгебраических дополнений
Матричные уравнения Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом: А*Х=В (1) Х*А=В (2) А*Х*С=В (3) В этих уравнениях А, В, С, Х - матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров. Если в уравнениях (1), (2) матрица А невырожденная, то их решения записываются следующим образом: Х=А-1*В, Х=В*А-1 Если в уравнении (3) матрицы А и С невырождены, то его решение записывается так: Х=А-1*В*С-1
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.186.131 (0.014 с.) |

 и любых чисел α, β:
и любых чисел α, β:






 и
и  коллинеарны тогда и только тогда, когда они пропорциональны, т.е. существует число α ≠ 0 такое, что
коллинеарны тогда и только тогда, когда они пропорциональны, т.е. существует число α ≠ 0 такое, что 
 называется число, обозначаемое
называется число, обозначаемое  и равное произведению их модулей и косинуса угла φ между ними, т.е.
и равное произведению их модулей и косинуса угла φ между ними, т.е. 
 и любых чисел α, β:
и любых чисел α, β: 



 определяется формулой
определяется формулой 

 координаты перемножаемых векторов
координаты перемножаемых векторов  орты координатных осей
орты координатных осей который обозначается
который обозначается  удовлетворяет следующим трем условиям:
удовлетворяет следующим трем условиям:

 образуют правую тройку, т.е. из конца вектора
образуют правую тройку, т.е. из конца вектора  к вектору
к вектору  виден против часовой стрелки.
виден против часовой стрелки.
 для любого вектора
для любого вектора  и любых чисел α, β:
и любых чисел α, β:




 называется число, обозначаемое
называется число, обозначаемое  и определяемое равенством
и определяемое равенством 
 умножается скалярно на третий вектор
умножается скалярно на третий вектор  .
.
 — правая, и со знаком «−», если тройка векторов — левая.
— правая, и со знаком «−», если тройка векторов — левая. 








 называется уравнением прямой в отрезках (a — абсцисса точки пересечения прямой с осью OX, b — ордината точки пересечения прямой с осью OY).
называется уравнением прямой в отрезках (a — абсцисса точки пересечения прямой с осью OX, b — ордината точки пересечения прямой с осью OY). .
.




 R:
R:





 разложение по i–ой строке
разложение по i–ой строке разложение по j–ому столбцу.
разложение по j–ому столбцу.
 min(m;n);
min(m;n); .
. где
где 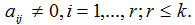
 не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:  , где 0 = (0,0,…,0). В противном случае строки матрицы называются линейно независимыми.
, где 0 = (0,0,…,0). В противном случае строки матрицы называются линейно независимыми. 2 и т.д.
2 и т.д. 0. Если таких миноров нет или они все равны нулю, то r(А) = k-1; если есть хотя бы один такой минор Мк
0. Если таких миноров нет или они все равны нулю, то r(А) = k-1; если есть хотя бы один такой минор Мк 






