
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование заменой переменных в определенном интегралеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Функция Теорема. Пусть функция
Рис.8.
Доказательство 1.По условию теоремы функция 2.Следовательно, имеет смысл сложная функция 3.В силу сделанных предположений, подынтегральные функции в обеих частях формулы 4.Пусть 5.Тогда для 6.В соответствии с формулой Ньютона- Лейбница:
Следовательно, Замечание. Если при вычислении неопределённого интеграла с помощью замены переменной следует возвращаться к старой переменной, то при вычислении определённого интеграла этого делать не нужно. При использовании формулы Интегрирование по частям в определенном интеграле Теорема. Если функции
Доказательство 1.Имеем 2.Все эти 3 интеграла существуют, так как по условию теоремы функции 3.На основании формулы Ньютона- Лейбница можно записать:
4.Сравним формулы п.1 и п.3 и сделаем вывод
Пример. Вычислить
Модуль Тема №10 Понятие квадратируемой фигуры, кубируемого тела и спрямляемой кривой Лекция №21 1. Определений понятия площади. 2. Квадратируемые фигуры. 3. Простейшие свойства площади. 4. Площадь криволинейной трапеции. 5. Площадь фигуры, расположенной под осью 6. Площадь фигуры в декартовых координатах. 7. Площадь фигуры, ограниченной снизу и сверху графиками функций.
8. Площадь фигуры, ограниченной кривой, заданной параметрическими уравнениями. Определение понятия площади
1. Для таких фигур понятие площади было достаточно изучено в школьном курсе геометрии. Теперь рассмотрим на плоскости произвольную фигуру 2. Ее граница или контур обозначается
3. Рассмотрим всевозможные многоугольники 4. Пусть 5. Множество площадей Обозначим точную верхнюю грань множества чисел 6. Аналогично, множество площадей Пусть 7. Эти границы Определение 2. Если границы
Квадратируемые области Приведенное определение 2 позволяет формулировать условие квадратируемости фигур или областей в виде двух соответствующих теорем. Теорема 1. Для того чтобы плоская фигура
Тогда этот предел
|
||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.100.99 (0.011 с.) |

 , заданная на промежутке
, заданная на промежутке 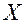 , называется непрерывно дифференцируемой на
, называется непрерывно дифференцируемой на  непрерывна на
непрерывна на  , а функция
, а функция 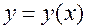 непрерывно дифференцируема на
непрерывно дифференцируема на  , причём
, причём  . Тогда справедлива формула
. Тогда справедлива формула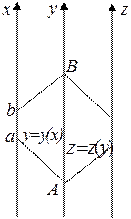
 . (*)
. (*) .
. непрерывны. Следовательно, оба интеграла формулы существуют.
непрерывны. Следовательно, оба интеграла формулы существуют.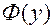 – какая – либо первообразная функции
– какая – либо первообразная функции  на интервале
на интервале  .
. имеет смысл сложная функция
имеет смысл сложная функция 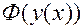 , которая является первообразной для функции
, которая является первообразной для функции  .
.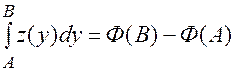 и
и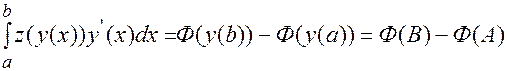 [15].
[15]. . Эта формула называется формулой замены переменной. Ч.т.д.
. Эта формула называется формулой замены переменной. Ч.т.д.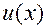 и
и  непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке  .
. на основании производной произведения двух непрерывно дифференцируемых функций и свойства определённого интеграла..
на основании производной произведения двух непрерывно дифференцируемых функций и свойства определённого интеграла.. .
. или
или [16].
[16].
 .
.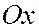 .
. Определение 1. Многоугольной областью или многоугольником называется произвольная плоская фигура, ограниченная одной или несколькими ломаными линиями (рис. 1.).
Определение 1. Многоугольной областью или многоугольником называется произвольная плоская фигура, ограниченная одной или несколькими ломаными линиями (рис. 1.).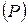 , представляющую собой ограниченную замкнутую область (рис. 2.).
, представляющую собой ограниченную замкнутую область (рис. 2.).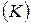 и представляет собой замкнутую кривую или несколько замкнутых кривых.
и представляет собой замкнутую кривую или несколько замкнутых кривых.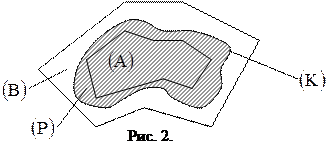
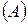 , целиком содержащиеся в фигуре
, целиком содержащиеся в фигуре  , и всевозможные многоугольники
, и всевозможные многоугольники  , целиком содержащие в себе фигуру
, целиком содержащие в себе фигуру  и
и 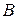 обозначают площади этих многоугольников. Очевидно, что
обозначают площади этих многоугольников. Очевидно, что 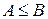 .
. многоугольников
многоугольников  и очевидно, что
и очевидно, что  .
. многоугольников
многоугольников  или любым
или любым  - точная нижняя грань множества чисел
- точная нижняя грань множества чисел  , очевидно, что
, очевидно, что 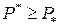 .
. , то плоская фигура
, то плоская фигура  .
. и
и  содержащихся в фигуре
содержащихся в фигуре 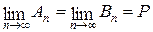 .
.


