
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование простейших иррациональных функций
Некоторые иррациональные и трансцендентные функции можно преобразовать к рациональным функциям и осуществлять интегрирование рациональных функций. Определение. Преобразование подынтегральной функции в рациональную функцию с помощью определенных подстановок называется рационализацией интегралов. Рационализация интеграла - это один из методов, с помощью которого устанавливается интегрируемость некоторых классов нерациональных функций. Рассмотрим интегрирование некоторых простейших иррациональных функций. Интеграл вида:
1. Такой интеграл рационализируется подстановкой:
2. Возведем обе части равенства в m степень:
3. Продифференцируем полученное выражение:
4. Таким образом, рассматриваемый интеграл принимает вид:
где Итак, полученный интеграл вычисляется по правилам интегрирования рациональных функций. Переход к старой переменной осуществляется с помощью подстановки
Интеграл вида:
1. В данном случае нельзя применить подстановку 2. Рационализация данного интеграла достигается с помощью одной из трех подстановок Эйлера. Модуль Тема №8 Неопределенный интеграл и его основные методы интегрирования Лекция №15 1. Три подстановки Эйлера. 2. Интегралы от некоторых тригонометрических функций. Примеры. 3. Интегралы от некоторых показательных функций. Примеры. Первая подстановка Эйлера Леонард Эйлер (1707-1783) – математик, механик, физик, астроном, член Петербургской академии наук. 1. Если а > 0, то применяется подстановка
2. Для определенности рассмотрим подстановку вида
3. Возведем в квадрат обе части записанного выражения, получим:
4. Дифференцируем обе части записанного выражения:
5. Поэтому
6. Так как теперь
где Вторая подстановка Эйлера 1. Если
2. Рассмотрим для определенности подстановку
3. Возведем в квадрат обе части этого равенства, получим:
4. Отсюда 5. Продифференцируем обе части выражения, получим:
6. При этом
7. Тогда данный интеграл примет вид:
где Третья подстановка Эйлера 1. Если квадратный трехчлен
2. Следовательно, подынтегральная функция рационально зависит от
3. Таким образом, пришли к рассмотренному выше интегралу I типа, который рационализируется с помощью подстановки Замечание. 1. Формула таблицы основных интегралов
2. Вычисление интегралов с помощью подстановок Эйлера обычно приводит к громоздким выражениям и трудоемким выкладкам. Поэтому их следует применять только, если данный интеграл не удается вычислить более коротким способом.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 941; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.33.41 (0.008 с.) |
 , где подынтегральная функция
, где подынтегральная функция  является сложной функцией от аргумента
является сложной функцией от аргумента  и
и  , где a,b,c,d,g- const, но
, где a,b,c,d,g- const, но ,
,  N.
N. .
.
 .
.
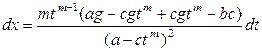 ,
, 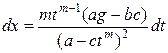 .
. =
= 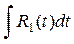 ,
,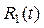 - рациональная функция от переменной t.
- рациональная функция от переменной t. .
. , где
, где  ,
,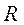 – сложная функция от
– сложная функция от 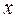 и
и 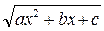 .
.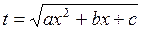 .
. .
. .
.
 ,
,  .
. или
или 
 .
. .
.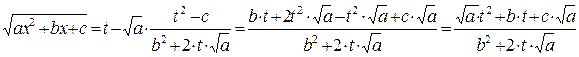 .
. и радикал рационально выражаются через
и радикал рационально выражаются через  , то подставим в данный интеграл вместо
, то подставим в данный интеграл вместо 
 и
и 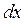 их значения:
их значения:
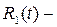 рациональная функция от переменной
рациональная функция от переменной 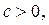 то для рационализации интеграла
то для рационализации интеграла  можно применить вторую подстановку Эйлера:
можно применить вторую подстановку Эйлера: .
. .
. или
или  или
или  .
.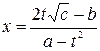 .
. ,
, или
или 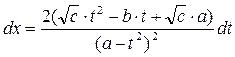 .
.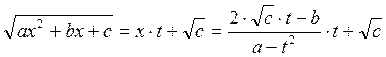 ,
, .
. =
= 
 рациональная функция от переменной
рациональная функция от переменной  имеет различные действительные корни
имеет различные действительные корни 
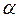 и
и  , то считая
, то считая 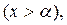 мы получаем:
мы получаем: .
. так, что
так, что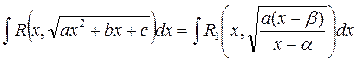 .
. Эта подстановка и представляет собой третью подстановку Эйлера.
Эта подстановка и представляет собой третью подстановку Эйлера.
 была получена с помощью первой подстановки Эйлера:
была получена с помощью первой подстановки Эйлера: 



