
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь криволинейной трапеции ⇐ ПредыдущаяСтр 10 из 10
Теорема 3. Пусть на плоскости
Доказательство 1. Изобразим рисунок в соответствии с условием теоремы.
2. Разобьем произвольно отрезок
и выберем на каждом частичном отрезке 3. Восстановим перпендикуляры в точках 4. Через полученные точки провести прямые, параллельные оси 5. Площадь криволинейной трапеции
6. Очевидно что при 7. С другой стороны, площадь ступенчатой фигуры является интегральной суммой 8. Так как по условию теоремы функция
9. Следовательно, и площадь криволинейной трапеции
Геометрический смысл теоремы: определенный интеграл от неотрицательной непрерывной функции Площадь фигуры расположенной под осью Ox Теорема 4. Пустьфункция
Доказательство 1. Изобразим рисунок в соответствии с условием теоремы.
2. Рассмотрим функцию 3. Эта функция неотрицательна и непрерывна на 4. Криволинейная трапеция, ограниченная сверху графиком функции 5. Следовательно, фигуры 6. Площадь криволинейной трапеции
7. Следовательно, по этой же формуле определяется площадь заданной трапеции по условию теоремы. ч. т. д.
Площадь фигуры в декартовой системе координат 1. Рассмотрим теперь более общий случай, когда некоторые части кривой 2.
3. Теперь в соответствии с двумя предыдущими теоремами площадь фигуры будет определяться так:
Площадь фигуры, ограниченной сверху и снизу Графиками функций 1. 2. Изобразим рисунок:
3. Так как обе функции неотрицательны, то площадь данной фигуры равна разности площадей двух криволинейных трапеций, ограниченных сверху соответственно графиками функций 4. Следовательно, площадь фигуры определяется по формуле:
Замечание. Данная формула будет справедлива тогда и только тогда, когда
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 768; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.129.100 (0.017 с.) |
 дана фигура, ограниченная отрезком
дана фигура, ограниченная отрезком  оси
оси  , прямыми
, прямыми  ,
,  и графиком непрерывной неотрицательной функции
и графиком непрерывной неотрицательной функции  на
на  .
.
 частей точками
частей точками
 произвольную точку
произвольную точку  , так чтобы
, так чтобы  .
. до пересечения с графиком.
до пересечения с графиком. приблизительно равна площади ступенчатой фигуры:
приблизительно равна площади ступенчатой фигуры: .
. , где
, где  площадь ступенчатой фигуры стремится к площади криволинейной трапеции.
площадь ступенчатой фигуры стремится к площади криволинейной трапеции. для определенного интеграла
для определенного интеграла  .
. непрерывна на отрезке
непрерывна на отрезке  по
по  .
. . ч. т. д.
. ч. т. д. , то есть кривая
, то есть кривая  или
или  .
.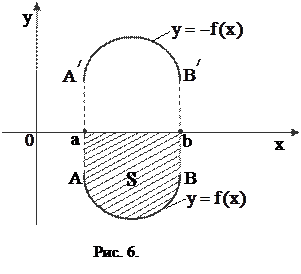
 .
. и
и  конгруэнтны (равны), и по свойству площадей их площади равны.
конгруэнтны (равны), и по свойству площадей их площади равны.


 .
. Изобразим рисунок:
Изобразим рисунок: или
или  [1], [15].
[1], [15]. Определим площадь фигуры, ограниченной снизу и сверху графиками функций
Определим площадь фигуры, ограниченной снизу и сверху графиками функций  ,
,  ,
,  , для любого
, для любого  , где
, где  ,
,  – непрерывные и неотрицательные функции на
– непрерывные и неотрицательные функции на  .
. .
. и
и 


