
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство необходимостиСодержание книги
Поиск на нашем сайте 1. Пусть площадь плоской фигуры
2. Так как фигура
3. Тогда 4. По свойству точной верхней грани множеств для любого 5. Перейдем к пределу в двойном неравенстве при 6. Так как 7. Переходя к пределу в последнем двойном неравенстве при
на основании теоремы о сжатой переменной следует. 8. В соответствии с п. 5 и п. 7 можно записать
Доказательство достаточности 1. Пусть существуют две последовательности многоугольников
Требуется доказать, что фигура 2. Пусть 3. Тогда площади многоугольников
4. По условию п. 1 5. Из неравенства п. 3 при переходе к пределу при Замечание. Иногда вместо многоугольников целесообразно рассматривать другие фигуры, квадратируемость которых уже установлена. Теорема 2. Если для фигуры Доказательство 1. Так как фигура 2. По свойству точной верхней грани последовательности можно записать неравенство 3. Так как по условию теоремы
на основании теоремы о сжатой переменной. 4. Так как по условию теоремы фигура 5. По свойству точной нижней грани последовательности можно записать неравенство 6. Так как по условию теоремы
на основании теоремы о сжатой переменной. 7. Таким образом, существуют две последовательности многоугольников Значит, на основании теоремы 1 фигура Вывод. Каждой квадратируемой фигуре Простейшие свойства площади 1. Конгруэнтные (равные) фигуры имеют равные площади. 2. Площадь части фигуры меньше, чем площадь всей фигуры. 3. Если плоская фигура
4. Пусть фигура прямых, параллельных осям координат на части. Если эти части представляют собой квадратируемые криволинейные трапеции, то по свойству 3 сама фигура
Замечание. Плоские фигуры, встречающиеся на практике, как, правило, могут быть разбиты на подобные трапеции, таким образом, можно вычислять площади практически любых плоский фигур [15].
|
||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 равна числу
равна числу  . Требуется доказать, что в нее можно вписать и около нее можно описать множество многоугольников, площади которых будут иметь общий предел, равный числу
. Требуется доказать, что в нее можно вписать и около нее можно описать множество многоугольников, площади которых будут иметь общий предел, равный числу  .
. .
. - точная верхняя грань площадей многоугольников
- точная верхняя грань площадей многоугольников  , которые вписаны в фигуру
, которые вписаны в фигуру  найдется содержащийся в фигуре
найдется содержащийся в фигуре  , такой что будет выполняться неравенство
, такой что будет выполняться неравенство  , (по аналогии
, (по аналогии  ). Здесь
). Здесь  .
. , получим
, получим  , на основании теоремы о пределе сжатой переменной.
, на основании теоремы о пределе сжатой переменной. - точная нижняя грань множества площадей многоугольников
- точная нижняя грань множества площадей многоугольников  , содержащиеся в фигуре
, содержащиеся в фигуре  , содержащий фигуру
, содержащий фигуру  , (на основании свойства нижней грани
, (на основании свойства нижней грани  ). Здесь
). Здесь 
 и
и  содержащихся в фигуре
содержащихся в фигуре  ,
,  , и, очевидно,
, и, очевидно,  .
. и
и  удовлетворяют неравенствам
удовлетворяют неравенствам .
. . А на основании определения 2 следует, что фигура
. А на основании определения 2 следует, что фигура  и
и  , содержащихся в
, содержащихся в  , то фигура
, то фигура  по условию квадратируема, то на основании теоремы 1 найдется такая последовательность многоугольников
по условию квадратируема, то на основании теоремы 1 найдется такая последовательность многоугольников  .
. (
( , то перейдя к пределу в неравенстве пункта 2, получим
, то перейдя к пределу в неравенстве пункта 2, получим
 квадратируема, то на основании теоремы 1 существует последовательность многоугольников, содержащих в себе фигуру
квадратируема, то на основании теоремы 1 существует последовательность многоугольников, содержащих в себе фигуру  (
( , то перейдя к пределу в двойном неравенстве пункта 5 получим
, то перейдя к пределу в двойном неравенстве пункта 5 получим
 и
и  , то квадратируемость двух из этих фигур
, то квадратируемость двух из этих фигур  , т. е. площадь обладает свойством аддитивности.
, т. е. площадь обладает свойством аддитивности.
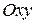 и может быть разбита с помощью
и может быть разбита с помощью



