
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неопределенный интеграл и его основные методы интегрированияСтр 1 из 10Следующая ⇒
Тема №8 Неопределенный интеграл и его основные методы интегрирования Лекция №10 1. Задачи восстановления функции по ее производной. 2. Неопределенный интеграл. 3. Свойства неопределенного интеграла. 4. Таблица основных интегралов. Задача восстановления функции по её производным Основной задачей дифференциального исчисления является отыскание производной заданной функции. Разнообразные задачи математического анализа и его многочисленные приложения в геометрии, физике, технике приводят к обратной задаче: по данной функции f (x) найти функцию F (x), производная которой равна f (x). Определение. Функция F (x) называется первообразной для функции f (x) на некотором множестве X, если для всех значений x Î X справедливо равенство: F '(x) = f (x). Пример №1. Функция F(x) = sin x есть первообразная для функции Пример №2. Функция F (x) = x 3 есть первообразная для функции Пример №3. Функция
Задача отыскания по данной функции f (x) её первообразной F (x) решаются неоднозначно. Действительно, если F (x) – первообразная для функции f (x), т.е. F' (x) =f (x), то и функция F (x) +С, где С – произвольная постоянная, также является первообразной для функции f (x), так как производная постоянной равна нулю, и Пример. Для функции Теорема. Всякие две первообразные одной и той же функции отличаются друг от друга на постоянную, определённую на одном и том же множестве X. Доказательство 1) Пусть F1 (x) и F2 (x) – некоторые первообразные функции f (x), определенные на промежутке X. 2) Введем вспомогательную функцию Ψ(x) = F2 (x)- F1 (x), и Ψ(x) – дифференцируема на X как производная разности двух дифференцируемых функций. 3) Причем, Ψ 4) На основании следствия к теореме Лагранжа функция Ψ(x) будет являться постоянной, так как её производная равна нулю на X, следовательно, Ψ(x) =C. 5) Поэтому Ψ(x) можно представить в виде Ψ(x) = F2 (x) - F1 (x) = C, следовательно, F2 (x) = F1 (x) + C. ч.т.д. Следствие. Если F (x) – какая-либо первообразная функции f (x)на промежутке X, то совокупность всех первообразных функции f (x)на промежутке X совпадает со множеством функции { F (x) +C }, C Î ℝ, C – const. Множество первообразных функции { F (x) +C } обозначается F (x) +C, C – const.
Чтобы выделить определенную первообразную Ф (x) для f (x)из { F (x) +C }, необходимо наложить некоторое дополнительное условие на функцию Ф (x). Обычно это начальное условие, т.е. требование, чтобы функция Ф (x) имела в какой-либо фиксированной точке x0 наперед заданное значение y0: F (x0) +C = Ф (x0) + y0.
Неопределенный интеграл Равенство F' (x) = f (x) можно записать
Определение №1. Если функция F (x) –первообразная функции f (x) на промежутке X, то множество функции F (x) +C, где C – произвольная постоянная, называется неопределенным интегралом от функции f (x)на этом промежутке X и обозначается символом Символ Определение №2. Восстановлением функции по её производной или, что то же, отыскание неопределенного интеграла по данной подынтегральной функции, называется интегрированием этой функции. Интегрирование представляет собой операцию обратную дифференцированию. Для того, чтобы проверить, правильно ли выполнено интегрирование, достаточно, продифференцировать результат и получить при этом подынтегральную функцию. Пример №1. Пример №2. Доказательство 1) Справедливость обеих формул следует из определения неопределенного интеграла. 2) Так 3) Аналогично: ч.т.д. 2. Пусть функция y=F (x) непрерывна на отрезке [ a, b ] и дифференцируема на (a,b), тогда выполняется равенство:
Доказательство Так как дифференциал функции
ч.т.д. 3. Если функции у = f1 (х)и y = f2 (x) имеют первообразные на [ a, b ], то и функция у = f 1(x) + f 2(x) будет иметь первообразную на [ a, b ], причем
Доказательство 1) Пусть 2) Тогда функция 3) Поэтому функция 4) По определению F 1 + F 2 будет первообразной для функции f 1 + f 2 на 5) А значит, 6) Сложим два интеграла п.1 7) В силу произвольности постоянных C 1, C 2 и C эти совокупности совпадают, и можно записать, что
ч.т.д. Замечание. Это свойство справедливо для любого конечного числа слагаемых функций. 4. Если функция у = f (x) имеет первообразную на [ a, b ] и k – const, k Î ℝ, то и функция у = k × f (x) будет иметь первообразную на [ a, b ], причем, если k ¹0, то Доказательство 1) Пусть 2) Значит, функция k × F (x) – непрерывна на [ a, b ] как произведение непрерывной функции на константу. 3) И функция 4) Следовательно, функция k × F (x) является первообразной для функции k × f (x) на [ a, b ]. 5) Поэтому 6) Исследуем неопределенный интеграл
7) В силу произвольности констант C и C 1 следует, что при k ¹ 0 эти совокупности совпадают, т.е.
ч.т.д. Таблица основных интегралов Часть формул этой таблицы непосредственно следует из определения интегрирования как операции, обратной дифференцированию и таблицы производных. 1. Доказательство 1) Так как dF (x)= f (x). 2) Тогда ч.т.д. 2. 3. Примеры 1). 2). 4. 5. Примеры 1). 2). 6. 7. Примеры 1). 2). 3). 8. Пример. 9. Пример. 10. Пример. 11. 12. Доказательство
1) 2) Пусть 3) Тогда 4) Поэтому 5) Пусть х Î(– а, + а), a > 0. 6) Тогда 7) Поэтому
8) Пусть х Î(а, +
9) Тогда 10) Поэтому 11) Значит, ч.т.д. 13.
Пример. 14. 15. Доказательство 1) Пусть x Î ℝ. 2) Тогда 3) Пусть x Î(– 4) Тогда 5) Поэтому 6) Пусть 7) Поэтому ч.т.д. 16. 17.
Замечание 1. Интегралы, содержащиеся в этой таблице, принято называть табличными. 2. Все формулы основной таблицы интегралов остаются справедливыми и в том случае, когда переменная интегрирования не является независимой, а представляет функцию от некоторой переменной
Модуль Тема №8 Лекция №11 1. Непосредственное интегрирование. Примеры. 2. Интегрирование подстановкой и заменой переменных. Примеры. 3. Формула интегрирования заменой переменной. Примеры. 4. Метод интегрирования по частям. Примеры. Непосредственное интегрирование Определение. Вычисление интегралов с помощью непосредственного использования таблицы интегралов и основных простейших свойств неопределенного интеграла называется непосредственным интегрированием. Примеры 1. 2. 3.
Доказательство
1) Из условия теоремы следует, что определены две сложные функции z 2) Функция F (y) дифференцируема и непрерывна на отрезке [ A, B ], так как является первообразной для функции z 3) Следовательно, функция F (y (x)) будет непрерывна на [ a, b ], как композиция непрерывных функций (как сложная функция от непрерывных функций). 4) Применим правило дифференцирования сложной функции, т.е. продифференцируем функцию F (y) и y (x).
5) Следовательно, функция F (y (x))является первообразной для функции 6) Тогда по определению неопределенного интеграла можно записать
ч.т.д. Доказательство 1. По правилу дифференцирования произведения двух функций на (a, b) можно записать:
2. Следовательно, из этого равенства можно записать
3. Первообразной функции 4. Из определения неопределенного интеграла можно записать:
5. По условию теоремы функция 6. Следовательно, исходя из п.2 можно заключить, что
ч.т.д. Замечание. Полученная формула позволяет свести вычисление интеграла Примеры 1.
2. 1) 2) Преобразуем интеграл
3) Тогда
Замечание. Иногда при вычислении неопределенного интеграла методом интегрирования по частям приходится пользоваться несколько раз. Пример. Модуль Тема №8 Лекция №12, 13 1. Интегрирование рациональных выражений. 2. Метод неопределенных коэффициентов. 3. Виды дробей. 4. Интегрирование простейших дробей I и II типа. Примеры. 5. Интегрирование простейших дробей III типа. Примеры. 6. Интегрирование простейших дробей IV типа. Примеры. Сведения из алгебры Определение. Дроби вида Теорема. Каждая рациональная функция представляется в виде суммы некоторого многочлена и конечного числа простых рациональных функций. 1. Рассмотрим рациональную функцию 2. Если 3. Пусть 4. Известно, что в разложении дроби
5. Множителю
5. Коэффициенты Виды простых дробей Простейшие дроби – это дроби следующих четырех типов: I тип: II тип: III тип: IV тип: Модуль Тема №8 Лекция №14 1. Интегрирование простейших иррациональных функций. Пример. 2. Интеграл вида 3. Интеграл вида Модуль Тема №8 Лекция №15 1. Три подстановки Эйлера. 2. Интегралы от некоторых тригонометрических функций. Примеры. 3. Интегралы от некоторых показательных функций. Примеры. Первая подстановка Эйлера Леонард Эйлер (1707-1783) – математик, механик, физик, астроном, член Петербургской академии наук. 1. Если а > 0, то применяется подстановка
2. Для определенности рассмотрим подстановку вида
3. Возведем в квадрат обе части записанного выражения, получим:
4. Дифференцируем обе части записанного выражения:
5. Поэтому
6. Так как теперь
где Вторая подстановка Эйлера 1. Если
2. Рассмотрим для определенности подстановку
3. Возведем в квадрат обе части этого равенства, получим:
4. Отсюда 5. Продифференцируем обе части выражения, получим:
6. При этом
7. Тогда данный интеграл примет вид:
где Третья подстановка Эйлера 1. Если квадратный трехчлен
2. Следовательно, подынтегральная функция рационально зависит от
3. Таким образом, пришли к рассмотренному выше интегралу I типа, который рационализируется с помощью подстановки Замечание. 1. Формула таблицы основных интегралов
2. Вычисление интегралов с помощью подстановок Эйлера обычно приводит к громоздким выражениям и трудоемким выкладкам. Поэтому их следует применять только, если данный интеграл не удается вычислить более коротким способом. Модуль Тема №9 Лекция №16 1. Задача о площади криволинейной трапеции. 2. Задача о пройденном пути. 3. Понятие определенного интеграла по Риману. 4. Суммы Дарбу и их геометрический смысл. Задача о пройденном пути 1.Определим путь 2.Разобьём 3.Пусть 4.Выберем в каждом из них произвольно момент времени 5.Вычислим скорость движения материальной точки в этот момент времени, т.е. найдём 6.Если дробление промежутка 7.Тогда путь, пройденный материальной точкой за i -й промежуток времени, будет приближённо равен 8.Тогда от момента времени 9.Это приближённое равенство будет тем точнее, чем мельче будет дробление отрезка времени 10.Точное равенство может быть достигнуто, если вычислить предел от этой суммы при Вывод: решение обеих задач свелось к одному и тому же вычислительному процессу. Можно было привести ещё целый ряд задач из других областей науки. Все они приводят к рассмотрению предела суммы вида Суммы Дарбу Гастон Дарбу – фр. математик (1842 - 1917).
1.Пусть функция 2.Обозначим через 3. Составим следующие суммы: 4.Эти суммы соответственно называются нижней и верхней суммами Дарбу функции 5. Из определения нижней и верхней граней функции Модуль Тема №9 Лекция №17 1. Свойства сумм Дарбу. 2. Необходимое и достаточное условия интегрируемости функции по Риману. 3. Интегрируемость непрерывной функции. 4. Интегрируемость монотонных функций. Свойства сумм Дарбу
Доказательство 1.Для доказательства свойства достаточно ограничиться присоединением к уже имеющимся точкам деления ещё одной точки деления
2.Пусть эта точка попадает между точками  и и 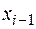 , т.е. , т.е.  и и  . .
Рис.3. 3.Так как то 4.Так как Ч.т.д.
Доказательство
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.56 (0.239 с.) |
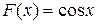 , так как " x Î ℝ: (sin x)'x = cos x.
, так как " x Î ℝ: (sin x)'x = cos x. .
. есть первообразная для функции
есть первообразная для функции  , на интервале (-1;1), так как в любой точке этого интервала
, на интервале (-1;1), так как в любой точке этого интервала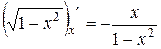 .
.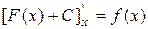 для любого числа С.
для любого числа С. первообразной является не только sin
первообразной является не только sin  , но и функция
, но и функция  , так как
, так как  .
.
 .
.
 имеет место тогда и только тогда, когда dF (x) = f (x) dx. Поэтому первообразную функции f (x) называют первообразной дифференциальной формы,
имеет место тогда и только тогда, когда dF (x) = f (x) dx. Поэтому первообразную функции f (x) называют первообразной дифференциальной формы,  , т.е.
, т.е. .
. = F (x) +C (читают: интеграл эф икс дэ икс), где f (x) – подынтегральная функция, f (x) dx – подынтегральное выражение, x – переменная интегрирования, C – постоянная интегрирования.
= F (x) +C (читают: интеграл эф икс дэ икс), где f (x) – подынтегральная функция, f (x) dx – подынтегральное выражение, x – переменная интегрирования, C – постоянная интегрирования. =
=  , неопределенный интеграл
, неопределенный интеграл 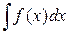 можно записать в других эквивалентных формах
можно записать в других эквивалентных формах  .
. . Утверждение верно на любом промежутке из
. Утверждение верно на любом промежутке из 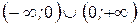 .
. , верно на любом промежутке из
, верно на любом промежутке из 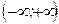 .
. .
.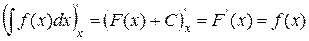 .
. или
или  , то есть неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной.
, то есть неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной. , то
, то .
. .
. ,
,  , где
, где  ,
,  – непрерывны на [ a, b ], а
– непрерывны на [ a, b ], а  и
и  – непрерывны на
– непрерывны на  будет непрерывна на [ a, b ] как сумма двух непрерывных на [ a, b ] функций.
будет непрерывна на [ a, b ] как сумма двух непрерывных на [ a, b ] функций. будет непрерывна как сумма двух непрерывных функций на (a, b).
будет непрерывна как сумма двух непрерывных функций на (a, b).
 .
.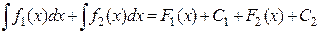 или
или  .
. .
. .
. , где функция F (x) непрерывна на [ a, b ], а функция
, где функция F (x) непрерывна на [ a, b ], а функция  непрерывна на (a, b).
непрерывна на (a, b). будет непрерывна на (a, b) по той же причине.
будет непрерывна на (a, b) по той же причине. .
. , где C=k × C 2.
, где C=k × C 2. .
.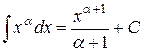 , a ¹ –1. Эта формула справедлива для любого промежутка, на котором имеет смысл степень xa.
, a ¹ –1. Эта формула справедлива для любого промежутка, на котором имеет смысл степень xa. .
. . Эта формула справедлива для любого промежутка, не содержащего x = 0.
. Эта формула справедлива для любого промежутка, не содержащего x = 0. . Эта формула справедлива для любого промежутка, удовлетворяющего неравенству f (x) ¹ 0.
. Эта формула справедлива для любого промежутка, удовлетворяющего неравенству f (x) ¹ 0. , так как квадратный трехчлен x 2 + x + 1 всюду положителен на ℝ.
, так как квадратный трехчлен x 2 + x + 1 всюду положителен на ℝ.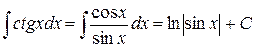 , верно на любом промежутке, где sin x ¹ 0.
, верно на любом промежутке, где sin x ¹ 0. , a ¹ –1, a > 0. Формула справедлива для любого промежутка из ℝ.
, a ¹ –1, a > 0. Формула справедлива для любого промежутка из ℝ. . Формула справедлива для произвольного промежутка.
. Формула справедлива для произвольного промежутка. , верно на любом промежутке.
, верно на любом промежутке. , верно на любом промежутке.
, верно на любом промежутке. , верно для любого промежутка.
, верно для любого промежутка. , верно для любого промежутка.
, верно для любого промежутка. , верно на любом промежутке из ℝ.
, верно на любом промежутке из ℝ. , верно на любом промежутке, удовлетворяющем неравенству x > 0.
, верно на любом промежутке, удовлетворяющем неравенству x > 0.
 , верно на любом промежутке из ℝ.
, верно на любом промежутке из ℝ. , верно для любого промежутка, на котором определен tg x.
, верно для любого промежутка, на котором определен tg x. , верно на любом промежутке, на котором определен
, верно на любом промежутке, на котором определен  .
. , верно на любом промежутке, где определен ctg x.
, верно на любом промежутке, где определен ctg x. , верно на любом промежутке, исключая х = 2p n, где n Î ℤ.
, верно на любом промежутке, исключая х = 2p n, где n Î ℤ. , a ¹ 0, верно для любого промежутка из ℝ.
, a ¹ 0, верно для любого промежутка из ℝ. , верно для любого промежутка из ℝ.
, верно для любого промежутка из ℝ. , верно для любого промежутка из ℝ..
, верно для любого промежутка из ℝ.. , a ¹ 0,верно для любого промежутка, не содержащего точек x = a и x = – a.
, a ¹ 0,верно для любого промежутка, не содержащего точек x = a и x = – a.
 .
. , a > 0.
, a > 0.
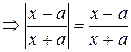 .
.
 (производная от неопределенного интеграла равна подынтегральной функции).
(производная от неопределенного интеграла равна подынтегральной функции). .
.
 .
. ), a > 0.
), a > 0. .
.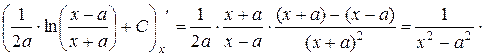
 ,
, 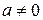 .
. , а ¹ 0. Формула справедлива для любого промежутка из интервала (–| a |, | a |), так как
, а ¹ 0. Формула справедлива для любого промежутка из интервала (–| a |, | a |), так как .
. , справедливо на любом промежутке из интервала (–4, 4).
, справедливо на любом промежутке из интервала (–4, 4). , формула справедлива для любого промежутка из интервала (–1, 1).
, формула справедлива для любого промежутка из интервала (–1, 1). , a ¹ 0, при x 2 + a 2 –справедлива для любого промежутка, при x 2 – a 2 – справедлива для любого промежутка, лежащего вне отрезка [–| a |, | a |].
, a ¹ 0, при x 2 + a 2 –справедлива для любого промежутка, при x 2 – a 2 – справедлива для любого промежутка, лежащего вне отрезка [–| a |, | a |].
 .
. , поэтому
, поэтому 
 .
.
 .
. .
. , верно на любом промежутке ℝ.
, верно на любом промежутке ℝ. , верно на любом промежутке из ℝ.
, верно на любом промежутке из ℝ.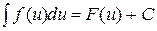 , где u = j (x).
, где u = j (x).
 , выражение справедливо на любом промежутке из ℝ, кроме x ¹ 0.
, выражение справедливо на любом промежутке из ℝ, кроме x ¹ 0.
 , выражение справедливо на любом промежутке из ℝ.
, выражение справедливо на любом промежутке из ℝ. =
=  , выражение справедливо на любом промежутке, на котором определена функция tg x.
, выражение справедливо на любом промежутке, на котором определена функция tg x.
 z (y (x)), где
z (y (x)), где  , F (y (x)), где
, F (y (x)), где  .
. .
. по определению первообразной.
по определению первообразной. .
. .
.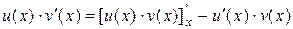 .
.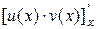 на [ a, b ] будет являться функция
на [ a, b ] будет являться функция 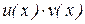 по определению первообразной.
по определению первообразной. .
.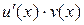 имеет первообразную на отрезке [ a, b ].
имеет первообразную на отрезке [ a, b ].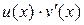 будет иметь первообразную на [ a, b ], т.е.
будет иметь первообразную на [ a, b ], т.е.  или
или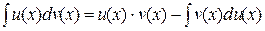 , или в более компактной форме
, или в более компактной форме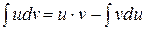 .
. к вычислению интеграла
к вычислению интеграла  , который может оказаться более простым.
, который может оказаться более простым.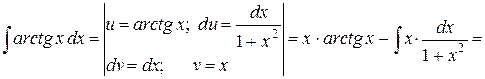
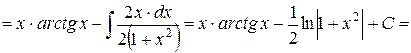
 –
– 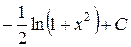 , выражение справедливо на любом промежутке из ℝ..
, выражение справедливо на любом промежутке из ℝ..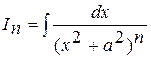 , n Î N, a = const, a Î ℝ.
, n Î N, a = const, a Î ℝ.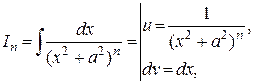
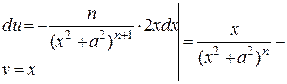
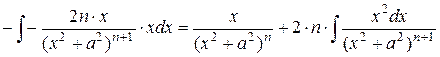 .
.
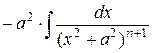 .
.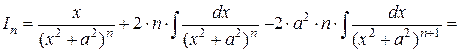
 .
.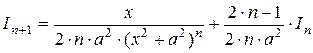 – рекуррентная формула для вычисления интеграла
– рекуррентная формула для вычисления интеграла 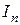 , при " n Î ℕ.
, при " n Î ℕ.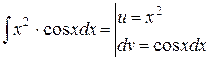

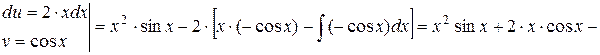
 , справедливо на любом промежутке из ℝ. Интеграл вычислен двукратным интегрированием по частям.
, справедливо на любом промежутке из ℝ. Интеграл вычислен двукратным интегрированием по частям. где
где  N называются простыми дробями,
N называются простыми дробями,  имеет отрицательный дискриминант.
имеет отрицательный дискриминант. где
где  - многочлен nой –степени,
- многочлен nой –степени,  - mой – степени, n,m
- mой – степени, n,m  N.
N. то функцию можно представить в виде
то функцию можно представить в виде 
 где
где  - многочлен степени n-m,
- многочлен степени n-m,  многочлен степени
многочлен степени  . Такое разложение рациональной функции получено в результате деления многочлена
. Такое разложение рациональной функции получено в результате деления многочлена 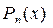 на
на  . Разложим многочлен
. Разложим многочлен  , где
, где  на простые дроби множителю
на простые дроби множителю  соответствует группа из k простых дробей:
соответствует группа из k простых дробей: .
. будет соответствовать группа из
будет соответствовать группа из  простых дробей:
простых дробей: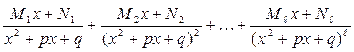 .
.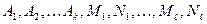 определяются методом неопределенных коэффициентов.
определяются методом неопределенных коэффициентов.
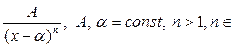 N.
N.
 N,
N, 
 . Примеры.
. Примеры. .
. .
. .
.
 ,
,  .
. или
или 
 .
. .
.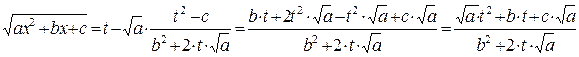 .
. и радикал рационально выражаются через
и радикал рационально выражаются через  , то подставим в данный интеграл вместо
, то подставим в данный интеграл вместо 
 и
и 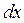 их значения:
их значения: =
= 
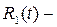 рациональная функция от переменной
рациональная функция от переменной 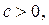 то для рационализации интеграла
то для рационализации интеграла  можно применить вторую подстановку Эйлера:
можно применить вторую подстановку Эйлера: .
. .
. или
или  или
или  .
.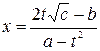 .
. ,
, или
или 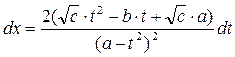 .
.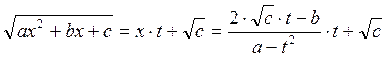 ,
, .
. =
= 
 рациональная функция от переменной
рациональная функция от переменной  имеет различные действительные корни
имеет различные действительные корни 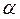 и
и  , то считая
, то считая 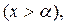 мы получаем:
мы получаем: .
.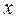 и от радикала
и от радикала  так, что
так, что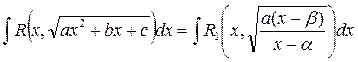 .
. Эта подстановка и представляет собой третью подстановку Эйлера.
Эта подстановка и представляет собой третью подстановку Эйлера.
 была получена с помощью первой подстановки Эйлера:
была получена с помощью первой подстановки Эйлера: 
 , пройденный материальной точкой за промежуток времени от момента
, пройденный материальной точкой за промежуток времени от момента  до T, если известна скорость движения точки как функции времени
до T, если известна скорость движения точки как функции времени  , т.е.
, т.е.  .
. на n произвольных отрезков точками
на n произвольных отрезков точками  В результате промежуток
В результате промежуток  разобьётся на частичные промежутки вида
разобьётся на частичные промежутки вида  , где
, где 
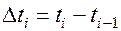 - величина i -го промежутка.
- величина i -го промежутка.

 .
. .
. .
.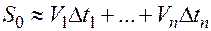 или
или  .
. .
. где
где  - величина наибольшего частичного промежутка времени, т.е.
- величина наибольшего частичного промежутка времени, т.е. 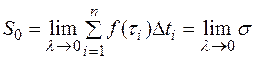 , где
, где 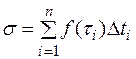 .
. . Изучение предела такой суммы приводит к понятию определённого интеграла.
. Изучение предела такой суммы приводит к понятию определённого интеграла.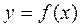 ограничена на отрезке
ограничена на отрезке  и
и  - разбиение этого отрезка точками
- разбиение этого отрезка точками 

 и
и 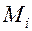 соответственно точную нижнюю и точную верхнюю грани этой функции на частичном отрезке
соответственно точную нижнюю и точную верхнюю грани этой функции на частичном отрезке  :
: 
 .
. ;
; 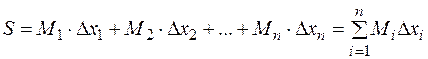 .
. для данного разбиения
для данного разбиения  отрезка
отрезка  или, если умножить все части двойного неравенства на
или, если умножить все части двойного неравенства на  и просуммировать по
и просуммировать по  от 1 до
от 1 до  , то
, то  или
или  . Любая интегральная сумма и суммы Дарбу для данного разбиения связаны этим неравенством. Очевидно, что
. Любая интегральная сумма и суммы Дарбу для данного разбиения связаны этим неравенством. Очевидно, что  .
. При добавлении точек разбиения отрезка нижняя сумма Дарбу может только увеличиться, а верхняя сумма Дарбу - только уменьшиться.
При добавлении точек разбиения отрезка нижняя сумма Дарбу может только увеличиться, а верхняя сумма Дарбу - только уменьшиться. .
.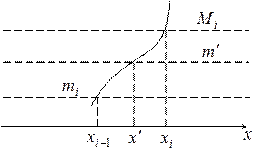

 ,
, и
и  , где
, где  - нижняя сумма Дарбу,
- нижняя сумма Дарбу,  - новая нижняя сумма Дарбу с дополнительной точкой разбиения
- новая нижняя сумма Дарбу с дополнительной точкой разбиения  =
=  , то
, то  , где
, где  - верхняя сумма Дарбу, а
- верхняя сумма Дарбу, а  - новая верхняя сумма Дарбу с добавлением точки
- новая верхняя сумма Дарбу с добавлением точки  Каждая нижняя сумма Дарбу не превосходит каждой верхней суммы Дарбу, хотя бы отвечающей другому разбиению, т.е.
Каждая нижняя сумма Дарбу не превосходит каждой верхней суммы Дарбу, хотя бы отвечающей другому разбиению, т.е. 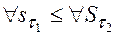 .
.


