
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегралы от некоторых тригонометрических функцийСодержание книги
Поиск на нашем сайте
I. Интеграл вида Определение. Рационализация этого интеграла достигается с помощью так называемой универсальной подстановкой: t = tg 1. Действительно, так как
3. Тогда интеграл примет вид:
где Замечание. Универсальная подстановка Пример. Вычислить интеграл 1. Воспользуемся универсальной подстановкой
2. Интеграл примет вид:
II. Интеграл вида 1. Для вычисления такого интеграла используется подстановка
2. В этом случае 3. Исследуемый интеграл примет вид
где III. Интеграл вида 1. Пусть 2. Тогда 3. Исследуемый интеграл примет вид:
где IV. Интеграл вида 1. Пусть 2. Тогда 3. Интеграл примет вид где V. Интеграл вида 1. Пусть
2. Поэтому 3. Интеграл примет вид: где Интегралы от показательных функций I. Интеграл вида: 1. Применим подстановку: 2. Прологарифмируем обе части записанного выражения по основанию 3. Продифференцируем обе части записанного выражения, получим: 4. Исходный интеграл принимает вид: где Пример. Вычислить интеграл II. Интеграл вида: 1. В данном случае интегрирование осуществляется с использованием метода интегрирования по частям.
2. При однократном применении формулы (*), степень многочлена 3. Если степень многочлена
III. Интегралы вида: 1. В данном случае интегрирование осуществляется с использованием метода интегрирования по частям
2. При однократном применении формулы (**) степень многочлена 3. Если степень многочлена
IV. Интегралы вида: Интегрирование осуществляется по формуле (*):
V. Интегралы вида: Интегрирование осуществляется по формуле (*): Модуль Тема №9 Определенный интеграл. Формула Ньютона - Лейбница Лекция №16 1. Задача о площади криволинейной трапеции. 2. Задача о пройденном пути. 3. Понятие определенного интеграла по Риману. 4. Суммы Дарбу и их геометрический смысл.
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.37.43 (0.005 с.) |

 , где
, где  функция от аргументов
функция от аргументов 
 , -p <
, -p < 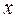 < p.
< p. ,
, 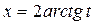 , то
, то 
 и
и  .
.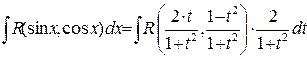 =
=  ,
, - рациональная функция от переменной
- рациональная функция от переменной  .
.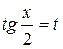 во многих случаях приводит к сложным вычислениям, так как при её применении
во многих случаях приводит к сложным вычислениям, так как при её применении  и
и  выражаются через
выражаются через  .
. .
. .
.
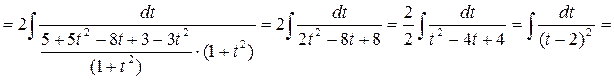
 верно на любом интервале, кроме
верно на любом интервале, кроме 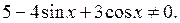
 .
.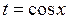 ,
, 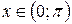 .
. ,
, 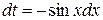 .
.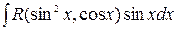 =
=  ,
, - рациональная функция от переменной
- рациональная функция от переменной  .
. .
. ,
,  .
.
 ,
,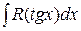 .
. .
.
 .
.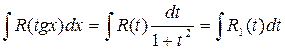 ,
, Q.
Q. , тогда
, тогда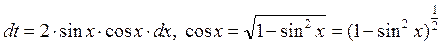 .
. .
.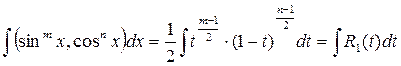 ,
, .
.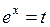 .
. , получим:
, получим: 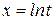 .
. .
.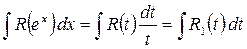 ,
, .
. 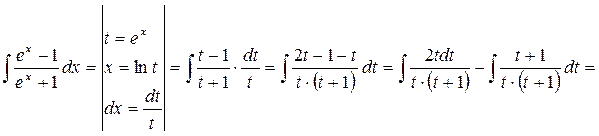
 верно налюбом промежутке из R.
верно налюбом промежутке из R.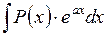 , где
, где  - многочлен некоторой натуральной степени,
- многочлен некоторой натуральной степени,  – константа из R.
– константа из R. ,
, 
 . (*)
. (*) , то формулу (*) нужно применять
, то формулу (*) нужно применять ,
, 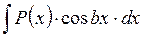 , где
, где 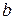 - константа из R.
- константа из R. ,
,  (**)
(**) .
. .
.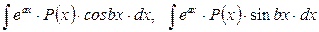 .
. .
.


