
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определенный интеграл с переменным верхним пределом
1.Ранее были рассмотрены определённые интегралы с постоянными пределами интегрирования
2.Если изменять, например, верхний предел интегрирования так, чтобы не выйти за границы  , то величина определённого интеграла будет меняться. Другими словами, интеграл с переменным верхним пределом представляет собой функцию своего верхнего предела. , то величина определённого интеграла будет меняться. Другими словами, интеграл с переменным верхним пределом представляет собой функцию своего верхнего предела.
Рис.7. 3.Рассмотрим интеграл 4.Обозначим эту функцию через Геометрически, функция Теорема. Если функция Доказательство 1.Пусть 2.Придадим аргументу 3.Тогда 4.Найдём разность 5.Если 6.Если
7.Таким образом, если 8. Если 9.При Следствие№1. Если функция Доказательство 1.Если функция 2.Тогда функция Следствие№2 (формула Ньютона- Лейбница). Если функция Доказательство 1.Известно, что если функция непрерывна на отрезке 2.Пусть 3.Известно, что любые первообразные одной и той же функции будут отличаться друг от друга на 4.Известно свойство определённого интеграла: 5.Тогда
6.Таким образом, для 7.Если Таким образом, определённый интеграл от непрерывной функции равен разности значений любой её первообразной, вычисленной от верхнего и нижнего пределов интегрирования. В этом заключается метод вычисления определённого интеграла. Замечание. Формула Ньютона- Лейбница выведена в предположении, что функция
|
||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 743; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.152.251 (0.005 с.) |
 и
и  .
.
 , где
, где  с постоянным нижним пределом
с постоянным нижним пределом  , и переменным верхним пределом
, и переменным верхним пределом  . Величина этого интеграла является функцией верхнего предела
. Величина этого интеграла является функцией верхнего предела 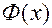 , т.е.
, т.е.  , чтобы не спутать с переменным верхним пределом
, чтобы не спутать с переменным верхним пределом  .
. непрерывна на отрезке
непрерывна на отрезке  , то функция
, то функция  и
и  или
или  .
. .
. приращение
приращение  так, чтобы
так, чтобы  не выходило за пределы
не выходило за пределы  .
.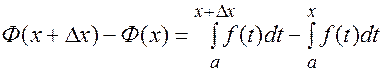 .
. , то
, то 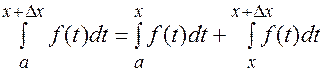 , тогда
, тогда  .
. , то рассмотрим
, то рассмотрим  , тогда
, тогда .
. = | на основании теоремы о среднем | =
= | на основании теоремы о среднем | = 
 .
. = | на основании теоремы о среднем | =
= | на основании теоремы о среднем | =  .
.
 . Перейдя к пределу в последнем равенстве при
. Перейдя к пределу в последнем равенстве при  . Ч.т.д.
. Ч.т.д. непрерывна на отрезке
непрерывна на отрезке  , так как на основании теоремы справедливо утверждение
, так как на основании теоремы справедливо утверждение  - её произвольная первообразная на этом отрезке, то
- её произвольная первообразная на этом отрезке, то  . Эта формула называется формулой Ньютона- Лейбница [3].
. Эта формула называется формулой Ньютона- Лейбница [3]. .
. , т.е.
, т.е.  или
или  где
где  .
. .
.
 .
. , то
, то  . Ч.т.д.
. Ч.т.д. непрерывна. При определённых условиях она будет справедлива и для разрывных функций.
непрерывна. При определённых условиях она будет справедлива и для разрывных функций.


