
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие определенного интеграла по РимануСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Пусть функция 2.Разобьём отрезок 3. 4.В каждом частичном отрезке разбиения выберем по одной точке 5.Составим интегральную сумму Римана: Определение 1. Если существует конечный предел от интегральной суммы Римана Определение 2 (“на языке последовательностей”, по Гейне). Функция Символически: Определение 3 (по Коши). Число Символически: Замечание. 1. Из определения определённого интеграла следует, что величина определенного интеграла зависит от вида функции 2. Из этого следует, что определённый интеграл не зависит от обозначения аргумента подынтегральной функции, т.е. от обозначения переменной интегрирования Теорема. Если функция Доказательство 1.Предположим противное, т.е. 2.За счёт произвольного выбора точек 3.Так как предел Замечание. Обратное утверждение неверно, т.е. условие ограниченности функции является необходимым, но недостаточным для интегрируемости функции.
Пример. Рассмотрим функцию Дирихле, определяемую на отрезке
0, если Эта функция ограничена на а) б) Следовательно, интегральная сумма при Суммы Дарбу Гастон Дарбу – фр. математик (1842 - 1917).
1.Пусть функция 2.Обозначим через 3. Составим следующие суммы: 4.Эти суммы соответственно называются нижней и верхней суммами Дарбу функции 5. Из определения нижней и верхней граней функции
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.119.128 (0.009 с.) |

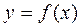 определена на
определена на  .
. на n-произвольных частей точками
на n-произвольных частей точками 
 - разбиение
- разбиение  - отрезок разбиения,
- отрезок разбиения,  - его длина и
- его длина и  - ранг разбиения
- ранг разбиения  , причём
, причём  .
. .
. , независящий от способа дробления промежутка
, независящий от способа дробления промежутка  , то функция
, то функция  называется интегрируемой по Риману на отрезке
называется интегрируемой по Риману на отрезке 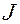 называют определённым интегралом функции
называют определённым интегралом функции  по отрезку
по отрезку  , т.е
, т.е  =
= 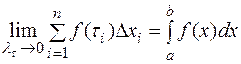 , где
, где  - нижний предел интегрирования,
- нижний предел интегрирования,  – верхний предел интегрирования,
– верхний предел интегрирования,  - переменная интегрирования,
- переменная интегрирования,  , у которой
, у которой  , соответствующая последовательность интегральных сумм
, соответствующая последовательность интегральных сумм  стремится к одному и тому же числу
стремится к одному и тому же числу  , т.е.
, т.е.  [9].
[9]. , независимо от выбора точек
, независимо от выбора точек  ).
). существует
существует  такое, что при
такое, что при  независимо от выбора точек
независимо от выбора точек 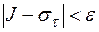 .
. .
. .
. и т.д.
и т.д.
 , где M – наперёд заданное большое число.
, где M – наперёд заданное большое число.

 1, если
1, если  =
=  , если
, если  - рациональные точки.
- рациональные точки. , если
, если  предела не имеет [10].
предела не имеет [10].

 и
и 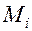 соответственно точную нижнюю и точную верхнюю грани этой функции на частичном отрезке
соответственно точную нижнюю и точную верхнюю грани этой функции на частичном отрезке  :
: 
 .
. ;
; 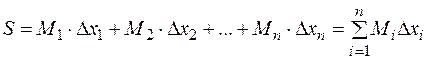 .
. отрезка
отрезка  или, если умножить все части двойного неравенства на
или, если умножить все части двойного неравенства на  и просуммировать по
и просуммировать по  от 1 до
от 1 до  , то
, то  или
или  . Любая интегральная сумма и суммы Дарбу для данного разбиения связаны этим неравенством. Очевидно, что
. Любая интегральная сумма и суммы Дарбу для данного разбиения связаны этим неравенством. Очевидно, что  .
.


