
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адсорбция на границе твердое тело – газ. Уравнение ЛенгмюраСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
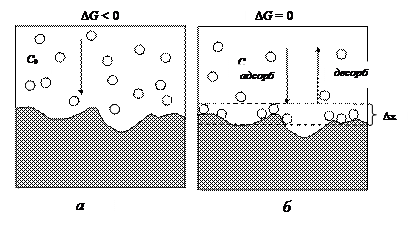
Исходя из молекулярно-кинетических представлений, американский физико-химик И. Ленгмюр предложил модель адсорбции в системе твердое тело – газ, исходя из следующих положений. Во-первых, физическая адсорбция на границе твердое тело – газ происходит не на всей поверхности, а на так называемых активных центрах – участках поверхности, активно взаимодействующих с адсорбтивом. Во-вторых, энергия адсорбции – одна и та же для молекул адсорбтива. В соответствии с этими положениями при достижении состояния динамического равновесия (рис. 15) скорость адсорбции становится равна скорости десорбции – процессу, обратному адсорбции.
Рис. 15. Схема процесса адсорбции газа на твердой поверхности: а) состояние системы до начала процесса адсорбции, концентрация газа с 0; б) состояние динамического равновесия между адсорбцией и десорбцией, концентрация газа в газовой фазе с; Dх – толщина адсорбционного слоя
Для твердого адсорбента обычно остается неизвестным поверхностное натяжение sт-г и толщина поверхностного слоя (Dх), в котором концентрируется адсорбат. Чтобы преодолеть возникшее затруднение в определении параметров адсорбционного слоя, поступают следующим образом. Измеряют концентрацию адсорбтивав u [л] газовой фазы до (с 0) и после (с) контакта газа с адсорбентом, когда наступит динамическое равновесие. Разность концентраций позволяет определить избыток адсорбата n [моль] на поверхности s [м2] адсорбента и величину адсорбции Гиббса: сs = (с – с0), n =(с – с0)×u [моль],
Обычно поверхность s твердого пористого адсорбента неизвестна. В этом случае экспериментальную величину адсорбции Гиббса рассчитывают в моль на грамм адсорбента: Г [моль/г].
Физико-химический процесс адсорбции можно представить уравнением: Ац + Ад ⇄ Ац×Ад, где Ац – активные центры на поверхности, Ад – адсорбтив в объеме газовой фазы, Ац×Ад – адсорбционные центры, занятые адсорбатом. Константа равновесия адсорбции выражается уравнением: К = [Ац×Ад]/[Ац]×[Ад], где К – константа равновесия, [Ад] = с моль/м3 – концентрация адсорбтива в объеме газовой фазы, [Ац×Ад] = a моль/м2 – концентрация активных центров, занятая адсорбатом, [Ац] =(a0 – a) моль/м2 – концентрация свободных активных центров на поверхности адсорбента, a0 моль/м2 – максимальная концентрация активных центров адсорбента, которые могут быть заполнены адсорбатом.
Воспользовавшись введенными обозначениями, получим выражение константы равновесия для адсорбционного процесса на поверхности:
или
Уравнение Ленгмюра может быть представлено в ином виде. В нем концентрация активных центров, занятая адсорбатом, выражена через давление газа:
где Кр = К / RT. Анализ уравнения Ленгмюра показывает, что при низких давлениях (концентрациях) газа произведением Кр×р по сравнению с единицей можно пренебречь (Кр×р << 1), тогда уравнение (2.17) примет вид: a = a0 ×Крр. В соответствии с этим уравнением наблюдается линейное нарастание количества адсорбированного вещества при увеличении давления газа. При высоких давлениях (Кр×р >> 1) достигается практически полное заполнение активных центров адсорбента. Количество адсорбированного вещества перестает зависеть от давления. Уравнение (2.17) принимает вид: a = a0 Взаимодействие адсорбтива с активными центрами адсорбента является обратимым процессом при соблюдении следующих условий: 1) на каждом адсорбционном центре может располагаться только одна молекула адсорбата, поэтому поверхность адсорбента покрывается мономолекулярным слоем адсорбата. 2) адсорбированные молекулы не взаимодействуют друг с другом. Типичная изотерма адсорбции Ленгмюра представлена на рис. 16.
Рис. 16. Изотерма адсорбции Ленгмюра
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.186.27 (0.011 с.) |

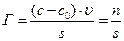 [моль/м2].
[моль/м2].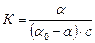 ,
,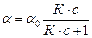 (адсорбционное уравнение Ленгмюра) (2.16)
(адсорбционное уравнение Ленгмюра) (2.16)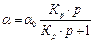 , (2.17)
, (2.17)



