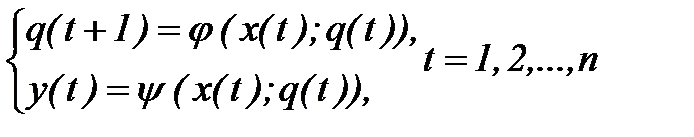Заглавная страница
Избранные статьи
Случайная статья
Познавательные статьи
Новые добавления
Обратная связь

ТОП 10 на сайте

Приготовление дезинфицирующих растворов различной концентрации

Техника нижней прямой подачи мяча.

Франко-прусская война (причины и последствия)

Организация работы процедурного кабинета

Смысловое и механическое запоминание, их место и роль в усвоении знаний

Коммуникативные барьеры и пути их преодоления

Обработка изделий медицинского назначения многократного применения

Образцы текста публицистического стиля

Четыре типа изменения баланса

Задачи с ответами для Всероссийской олимпиады по праву

Мы поможем в написании ваших работ!

ЗНАЕТЕ ЛИ ВЫ?

Влияние общества на человека

Приготовление дезинфицирующих растворов различной концентрации

Практические работы по географии для 6 класса

Организация работы процедурного кабинета

Изменения в неживой природе осенью

Уборка процедурного кабинета

Сольфеджио. Все правила по сольфеджио

Балочные системы. Определение реакций опор и моментов защемления

Главная Избранные Случайная статья Познавательные Новые добавления Обратная связь FAQ

Можно ли нарисовать картинки, не отрывая карандаша от бумаги и проводя каждую линию ровно один раз. Какие из них являются эйлеровыми графами.

⇐ ПредыдущаяСтр 11 из 12Следующая ⇒

0)	1)	2)
3)	4)	5)
6)	7)
8)	9)

3.5.2.

Задайте граф геометрически и решите задачу:

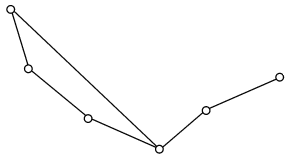
Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту ровно один раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист:

0) не с него начал и не на нем закончил?

1) с него начал, но не на нем закончил?

2) с него начал и на нем закончил?

3) Дан кусок проволоки длиной 120 см. Можно ли, не ломая проволоки, изготовить каркас куба с ребром 10 см?

4) В стране Озерная 7 озер, соединенных между собой 10 непересекающимися каналами, причем от любого озера можно доплыть до любого другого. Сколько в этой стране островов?

5) Можно ли построить 3 дома, вырыть 3 колодца и соединить тропинками каждый дом с каждым колодцем так, чтобы тропинки не пересекались?

6) Можно ли составить решетку размером 4´4 (длина стороны клетки = 1):

а) из 5 ломаных длины 8? б) из 8 ломаных длины 5?

7) В квадрате отметили 20 точек и соединили их непересекающимися отрезками друг с другом и с вершинами квадрата так, что квадрат разбился на треугольники. Сколько получилось треугольников?

8) В стране несколько городов, некоторые пары городов соединены беспосадочными рейсами одной из N авиакомпаний, причем из каждого города есть ровно по одному рейсу каждой из авиакомпаний. Известно, что из любого города можно долететь до любого другого (возможно, с пересадками). Из-за финансового кризиса был закрыт N- 1рейс, но ни в одной из авиакомпаний не закрыли более одного рейса. Докажите, что по-прежнему из любого города можно долететь до любого другого.

9) В Совершенном городе шесть площадей. Каждая площадь соединена прямыми улицами ровно с тремя другими площадями. Никакие две улицы в городе не пересекаются. Из трёх улиц, отходящих от каждой площади, одна проходит внутри угла, образованного двумя другими. Начертите возможный план такого города.

3.5.3. Граф задан геометрически. Выпишите гамильтонов цикл у данного графа, если он есть:

0) Решение: 1) Решение:

2) Решение: 3) Решение:

4) Решение: 5) Решение:

6) Решение: 7) Решение:

8) Решение: 9) Решение:

Глава 4. Автоматы

Система A=(X;Q;Y;j;y) называется конечным автоматом,
где

X = {a1,…,am} - входной алфавит с входными сигналами,

Q = {q1,…,qn} - множество состояний,

Y = {b1,…,bp} - выходной алфавит с выходными сигналами,

j: X ´ Q ® Q - функция переходов, т.е. j(x, q) ÎQ "xÎX; "qÎQ,

y: X ´ Q ® Y - функция выходов, т.е. y(x, q) Î Y "xÎX; "qÎQ.

Существуют следующие способы задания автоматов:

- с помощью таблицы. Функции j и y задаются таблицей, строки которой соответствуют буквам входного алфавита, а столбцы – состояниям. В пересечении строки a_j и столбца q_i помещается состояние
y (a_j, q_i), в которое переходит автомат из состояния q_i под воздействием входного символа a_j, и значение j (a_j, q_i), которое при этом появляется на выходе;

- в виде диаграммы. Состояния q_i изображаются на плоскости кружками, из которого проводится стрелка в q_u, если автомат, находящийся в состоянии q_i, при подаче некоторого входного символа может быть переведен в состояние q_u;

- совокупностью четверок вида: q_ia_j ® q_la_p,. Если на вход автомата, находящегося в состоянии q_i, в момент времени t подается символ a_j, то на выходе автомата в этот же момент времени появляется символ a_p, и в следующий момент времени t+1 автомат будет находиться в состоянии q_l.

- в виде системы булевых функций. Каждому q_j ÎQ взаимно-однозначно ставится в соответствие двоичная последовательность длины r - двоичный код a(q) = z₁z₂…z_r. Аналогично каждому a_iÎX и каждому b_k ÎY ставим взаимно-однозначно в соответствие двоичные последовательности b(a) = x₁x₂…x_k; g(b) = y₁y₂…y_s.В результате автомат будет задан системой булевых функций {j₁,j₂,…,j_r,y₁,y₂,…,y_s};

- в виде канонических уравнений. Если в момент времени t=1,2,… на вход автомата A=(X; Q; Y; j; y) последовательно подаются входные символы x(t)ÎX и при этом автомат находится в состоянии q(t)ÎQ, то под воздействием символа x(t) автомат перейдет в новое состояние q(t+1)ÎQ и выдаст выходной сигнал y(t). Величины x(t), y(t), q(t), q(t+1) связаны между собой следующими каноническими уравнениями:

К задачам теории автоматов относятся: задачи анализа и синтеза автоматов, задачи полноты, минимизации, эквивалентных преобразований автоматов и другие.

Задачи анализа автоматов

Задача анализа состоит в том, чтобы по заданному описанию автомата (или по неполным данным об автомате и его функционированию) задать его поведение и установить те или иные его свойства.

Примеры выполнения заданий

1. Работа автомата задана таблично и выдает на выходе символ “*”, всякий раз, когда во входном алфавите встречается цепочка из комбинаций символов 0, 1, 2. Опишите работу автомата с помощью совокупности четверок. X = {0, 1, 2}, Y = {0, 1, 2} и Q = {q₀, q₁, q₂, q₃}. Определите, что распознает автомат.

Символы алфавита	С о с т о я н и я
q₀	q₁	q₂	q₃
	q₁,1	q₂,1	q₀,0	q₀,0
	q₀,1	q₀,1	q₀,1	q₀,1
	q₀,2	q₀,2	q₃,1	q₀,*

Решение:

q₀0® q₁1 q₀1® q₀1 q₀2® q₀2

q₁0® q₂1 q₁1® q₀1 q₁2® q₀2

q₂0® q₀0 q₂1® q₀1 q₂2® q₃1

q₃0® q₀0 q₃1® q₀1 q₃2® q₀*

Автомат распознает цепочку вида: 1111*

2. Описание автомата - двоичного сумматора последовательного действия, задано с помощью совокупности четверок. X= {00, 01, 10, 11},
Y = {0, 1}, Q = {q₀, q₁}. Опишите работу автомата с помощью диаграммы.

q₀<0,0> → q₀0 q₀<0,1> → q₀1 q₀<1,0> → q₀1 q₀<1,1> → q₁0

q₁<0,0> → q₀1 q₁<0,1> → q₁0 q₁<1,0> → q₁0 q₁<1,1> → q₁1

Решение.

q₁

(00,0)Ú(01,1)Ú(10,1) (01,0)Ú(10,0)Ú(11,1)

(11,0)

q₁

q₀

(00,1)

Задания для самостоятельного выполнения

4.1.1. Работа автомата задана с помощью совокупности четверок и выдает на выходе символ “ * ”, всякий раз, когда во входной последовательности алфавита {a, b} встречается цепочка символов. Определите, что распознает автомат. Опишите работу автомата таблично.

0)

q₀b → q₀b q₀a → q₁a q₁b → q₂b q₁a → q₀b q₂b → q₃b q₂a → q₀b q₃b → q₀b q₃a → *

1)

q₀b → q₁b q₀a → q₀b q₁b → q₀b q₁a → q₂a q₂b → q₃b q₂a → q₀b q₃b → q₀b q₃a → *

2)

q₀a → q₁a q₀b → q₀a q₁a → q₂a q₁b → q₀a q₂a → q₀a q₂b → q₃b q₃a → q₀a q₃b → *

3)

q₀b → q₁b q₀a → q₀b q₁b → q₂b q₁a → q₀b q₂b → q₀b q₂a → q₃a q₃b → q₀b q₃a → *

4)

q₀a → q₁a q₀b → q₀a q₁a → q₂a q₁b → q₀a q₂a → q₃a q₂b → q₀a q₃a → q₀a q₃b → *

5)

q₀b → q₁b q₀a → q₀b q₁b → q₂b q₁a → q₀b q₂b → q₃b q₂a → q₀b q₃b → q₀b q₃a → *

6)

q₀a → q₀a q₀b → q₁b q₁a → q₀a q₁b → q₂b q₂a → q₀a q₂b → q₃b q₃a → q₀a q₃b → *

7)

q₀b → q₀b q₀a → q₁a q₁b → q₀b q₁a → q₂b q₂b → q₀b q₂a → q₃b q₃b → q₀b q₃a → *

8)

q₀a → q₁a q₀b → q₀b q₁a → q₀a q₁b → q₂b q₂a → q₃a q₂b → q₀b q₃a → q₀a q₃b → *

9)

q₀a → q₀a q₀b → q₁b q₁a → q₂a q₁b → q₀a q₂a → q₃b q₂b → q₀a q₃a → q₀a q₃b → *

Решение:

Символы алфавита С о с т о я н и я

q₀ q₁ q₂ q₃

a

b

4.1.2. Работа автомата задана таблично и выдает на выходе символ “&”, всякий раз, когда во входном алфавите встречается цепочка символов. Определите, что распознает автомат. Опишите работу автомата с помощью совокупности четверок.

0)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

О q₀,О q₂,О q₀,О q₀,О

К q₁,К q₀,О q₀,О q₀,О

Т q₀,О q₀,О q₃,Т q₀&

1)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

С q₀,С q₂,С q₀,С q₀,С

О q_1,О q₀,С q₀,С q₀,С

А q₀,С q₀,С q₃,А q₀&

2)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

М q₀,М q₀,М q₃,М q₀&

А q₀,М q₂,А q₀,М q₀,М

С q₁,С q₀,М q₀,М q₀,М

3)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

А q₀,А q₂,А q₀,А q₀,А

Д q₁,Д q₀,А q₀,А q₀,А

Р q₀,А q₀,А q₃,Р q₀&

4)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

О q₀,О q₂,О q₂,О q₀,О

Р q₁,Р q₀,О q₂,О q₀,О

М q₀,О q₀,О q₃,М q₀&

5)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

Р q₀,Р q₀,О q₃,Р q₀&

М q₁,М q₀,О q₀,О q₀,О

И q₀,Р q₂,И q₀,О q₀,О

6)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

А q₀,А q₂,А q₀,А q₀А

П q₁,П q₀,А q₀,А q₀,А

Р q₀,А q₀,А q₃,Р q₀&

7)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

М q₀,М q₀,М q₃,М q₀&

И q₀,М q₂,И q₀,М q₀,М

Р q₁,Р q₀,М q₀,М q₀,М

8)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

Р q₀,Р q₀,Р q₃,Р q₀&

У q₀,Р q₂,У q₀,Р q₀,Р

Т q₁,Т q₀,Р q₀,Р q₀,Р

9)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

Л q₀,Л q₂,Л q₀,Л q₀,Л

Т q₁,Т q₀,Л q₀,Л q₀,Л

Я q₀,Л q₀,Л q₃,Я q₀&

Решение:

q₀ → q₁ → q₂ → q₃ →

q₀ → q₁ → q₂ → q₃ →

q₀ → q₁ → q₂ → q₃ →

4.1.3. Работа автомата задана с помощью диаграммы и выдает на выходе символ “*", всякий раз, когда во входном алфавите встречается цепочка символов. Определите, что распознает автомат. Опишите работу автомата с помощью совокупности четверок.

0)

(б, б) (К, б) Ú (б, *)

q₀

q₁

(К, К)

1)

(м, м) (с, м) Ú (м, *)

q₀

q₁

(с, с)

2)

(б, б) (М, б) Ú (б, *)

q₀

q₁

(М, М)

3)

(г, г) (к, г) Ú (г, *)

q₀

q₁

(к, к)

4)

(б, б) (Г, б) Ú (б, *)

q₀

q₁

(Г, Г)

5)

(м, м) (д, м) Ú (м, *)

q₀

q₁

(д, д)

6)

(г, г) (м, г) Ú (г, *)

q₀

q₁

(м, м)

7)

(б, б) (Т, б) Ú (б, *)

q₀

q₁

(Т, Т)

8)

(а, а) (г, а) Ú (а, *)

q₀

q₁

(г, г)

9)

(м, м) (к, м) Ú (м, *)

q₀

q₁

(к, к)

Решение:

q₀ → q₁ →

q₀ → q₁ →

4.2. Задачи синтеза автоматов

Задача синтеза автоматов состоит в построении автомата с наперед заданным поведением или функционированием.

Примеры выполнения заданий

1. Постройте конечный автомат, воспринимающий на входе двоичную последовательность и выдающий на выходе специальный символ
‘ *’, если во входной последовательности подряд встретится 4 единицы. В остальных случаях автомат на выходе повторяет входной символ.

Решение.

q₀0® q₀0 q₀1® q₁1 q₁0® q₀0 q₁1® q₂1 q₂0® q₀0 q₂1® q₃1 q₃0® q₀0 q₃1® q₀*

2. Постройте конечный автомат таблично, представляющий двоичный сумматор последовательного действия.

Решение. Обозначим через q₀ и q₁ его состояния, соответствующие отсутствию и наличию переноса.

Символы алфавита Состояния

x₁ x₂ q₀ q₁

q₀,0 q₀,1

q₀,1 q₁,0

q₀,1 q₁,0

q₁,0 q₁,1

Задания для самостоятельного выполнения

4.2.1. Постройте конечный автомат, выдающий на выходе символ “!”, всякий раз, когда во входной двоичной последовательности встречается:

0) последовательность 0000;

1) последовательность 1111;

2) последовательность 0110;

3) последовательность 0111;

4) последовательность 1000;

5) последовательность 0011;

6) последовательность 0010;

7) последовательность 1110;

8) последовательность 0001;

9) последовательность 1100.

4.2.2. Постройте конечный автомат, выдающий на выходе символ “♫”, всякий раз, когда во входной последовательности в алфавите

0) {А, н, ю, т} встречается имя “Анюта”;

1) {А, л, е, ш} встречается имя “Алеша”;

2) {И, р, н, а} встречается имя “Ирина”;

3) {С, а, ш} встречается имя “Саша”;

4) {Д, а, я, н} встречается имя “Даяна”;

5) {Н, и, а} встречается имя “Нина”;

6) {А, н, ж, е, л} встречается имя “Анжела”;

7) {А, н, т, о} встречается имя “Антон”;

8) {С, е, р, ж, а} встречается имя “Сережа”;

9) {Л, и, я} встречается имя “Лилия”.

⇐ Предыдущая 3 4 5 6 7 8 9 101112 Следующая ⇒

Поделиться:

Читайте также:

Техника прыжка в длину с разбега

Тактические действия в защите

История Олимпийских игр

История развития права интеллектуальной собственности

Последнее изменение этой страницы: 2016-09-19; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы!

infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.106.100 (0.098 с.)