
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Треугольник Паскаля. Бином НьютонаСодержание книги
Поиск на нашем сайте
Составим таблицу значений сочетаний
Легко заметить, что коэффициенты в правых частях этих формул взяты из соответствующих строк треугольника Паскаля. Оказывается, при любом натуральном n справедлива формула Ньютона:
Правую часть формулы называют разложением степени бинома. Если вычисляется (а - b)n = (a + (-b))n, то далее знаки чередуются. Задания для самостоятельного выполнения 1. Запишите разложение бинома:
2. Вычислите без калькулятора:
3. Запишите разложение бинома:
Зачетные задания по теме «Комбинаторика» Задание 1. 0) Из города А в город В ведут пять дорог, а из города В в город С – три дороги. Сколько путей, проходящих через В, ведут из А в С? 1) Из двух спортивных обществ, насчитывающих по 100 фехтовальщиков каждое, надо выделить по одному фехтовальщику для участия в состязании. Сколькими способами может быть сделан этот выбор? 2) Имеется пять видов конвертов без марок и четыре вида марок одного достоинства. Сколькими способами можно выбрать конверт с маркой для посылки письма? 3) Сколькими способами можно выбрать гласную и согласную буквы из слова «камзол»? 4) Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»? 5) Бросают игральную кость с шестью гранями и запускают волчок, имеющий восемь граней. Сколькими различными способами они могут упасть? 6) На вершину горы ведут пять дорог. Сколькими способами •турист может подняться на гору и спуститься с нее? То же самое при условии, что спуск и подъем происходят по разным путям. 7) На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз? 8) Сколькими способами можно указать на шахматной доске два квадрата – белый и черный? А если нет ограничений на цвет выбранных квадратов? 9) Из 12 слов мужского рода, 9 женского и 10 среднего надо выбрать по одному слову каждого рода. Сколькими способами может быть сделан этот выбор? Задание 2. 0) В местком избрано 9 человек. Из них надо выбрать председателя, заместителя председателя, секретаря и культорга. Сколькими способами это можно сделать? 1) Из состава конференции, на которой присутствует 52 человека, надо избрать делегацию, состоящую из 5 человек. Сколькими способами это можно сделать? 2) Автомобильные номера состоят из одной, двух или трех букв и четырех цифр. Найти число таких номеров, если используются 32 буквы русского алфавита. 3) Сколько различных перестановок можно получить, переставляя буквы в слове «математика»? В слове «парабола»? 4) В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? Сколькими способами можно купить 8 открыток? 5) Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них' было не менее 2 женщин. Сколькими способами это можно сделать? 6) Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки? 7) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз? 8) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно один туз? 9) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно два туза?
Глава 3. Графы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 627; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.45.90 (0.006 с.) |

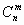 для n,m = 0,1,2,3,4,5,6,7.
для n,m = 0,1,2,3,4,5,6,7.
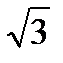 )4;
)4;
 )4;
)4;
 + 2y) 4;
+ 2y) 4;
 )4;
)4;
 )4;
)4;
 + 4y) 4;
+ 4y) 4;
 )4;
)4;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
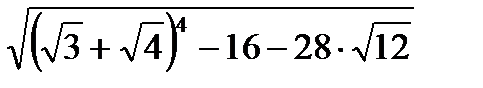 ;
;
 ;
;
 ;
;
 ;
;
 ;
;



