Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
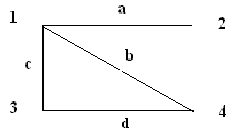
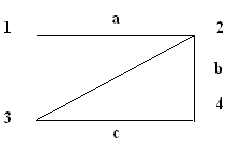
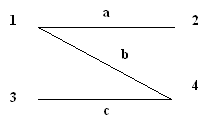
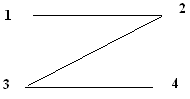
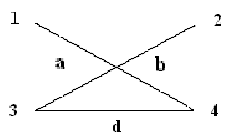
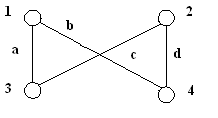
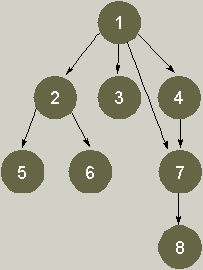
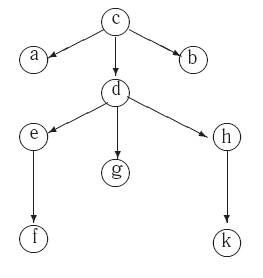
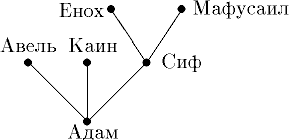
Определите, являются ли данные графы деревьями, почему?Содержание книги
Поиск на нашем сайте
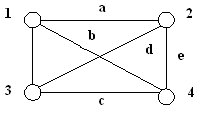
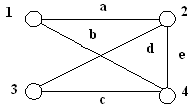
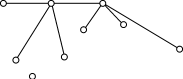
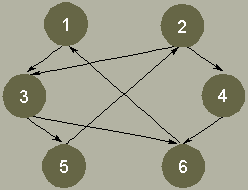
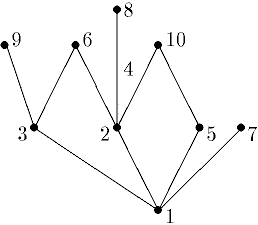
3.1.5. Определите виды графов и подсчитайте валентность вершин:
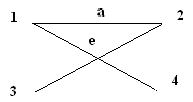
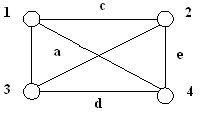
3.1.6. Определите виды графов и подсчитайте валентность вершин:
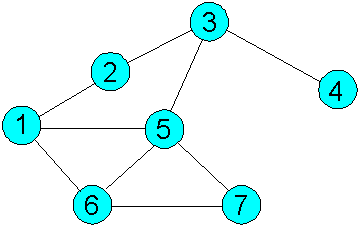
3.1.7. Решите задачи по вычислению валентности вершин графа: 0) В одной компании из 7 человек: Саша дружит с Леной и Алешей, Надя с Колей, Ваня с Сашей и Колей. Какова валентность вершин графа? 1) В государстве 100 городов, и из каждого из них выходит 4 дороги. Сколько всего дорог в государстве? 2) В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 - по 4 друга, а 10 - по 5 друзей? 3) В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы было 4 телефона, каждый из которых соединен с тремя другими, 8 телефонов, каждый из которых соединен с шестью, и 3 телефона, каждый из которых соединен с пятью другими? 4) - У меня зазвонил телефон. - Кто говорит? - Слон... А потом позвонил Крокодил... А потом позвонили Зайчатки... А потом позвонили Мартышки... А потом позвонил Медведь... А потом позвонили Цапли... Итак, у Слона, Крокодила, Зайчаток, Мартышек, Медведя, Цапель и у меня установлены телефоны. Каждые два телефонных аппарата соединены проводом. Как сосчитать, сколько для этого понадобилось проводов? Указание: заметьте, каждый провод соединяет два аппарата.
5) У короля 19 баронов-вассалов. Может ли оказаться так, что у каждого вассального баронства 1, 5 или 9 соседних баронств? 6) Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог? 7) Джон, приехав из Диснейленда, рассказывал, что там на заколдованном озере имеются 7 островов, с каждого из которых ведет 1, 3 или 5 мостов. Верно ли, что хотя бы один из этих мостов обязательно выходит на берег озера? 8) Можно ли нарисовать на плоскости 9 отрезков так, чтобы каждый пересекался, ровно с тремя другими? 9) Резидент одной иностранной разведки сообщил в центр о готовящемся подписании ряда двусторонних соглашений между пятнадцатью бывшими республиками СССР. Согласно его донесению, каждая из них заключит договор ровно с тремя другими. Заслуживает ли резидент доверия? Указание: подсчитайте двумя способами число подписей под всеми двусторонними соглашениями. И подумайте, может ли оно быть нечётным? 3.1.8. Решите задачи по вычислению валентности вершин графа: 0) В системе связи, состоящей из 2001 абонентов, каждый абонент связан ровно с n другими. Определите все возможные значения n. Указание: Посчитайте количество пар связанных абонентов и покажите, что n - четно. 1) Докажите, что не существует графа с пятью вершинами, степени которых равны 4, 4, 4, 4, 2. 2) В классе 20 учеников, причем каждый дружит не менее, чем с 14-ю другими. Можно ли утверждать, что найдутся четыре ученика, которые все дружат между собой? Указание У одного из учеников 14 друзей. Достаточно выбрать из них трех попарно знакомых. 3) В сказочной стране Перра-Терра среди прочих обитателей проживают Карабасы и Барабасы. Каждый Карабас знаком с шестью Карабасами и девятью Барабасами. Каждый Барабас знаком с десятью Карабасами и семью Барабасами. Кого в этой стране больше — Карабасов или Барабасов? 4) Можно ли 77 телефонов соединить между собой проводами так, чтобы каждый был соединён ровно с пятнадцатью? 5) На кошачьей выставке каждый посетитель погладил ровно трех кошек. При этом оказалось, что каждую кошку погладили ровно три посетителя. Докажите, что посетителей было ровно столько же, сколько кошек. Указание: мысленно натяните ниточки между каждой кошкой и погладившим её посетителем.
6) На третье занятие кружка по математике пришло 17 человек. Может ли случиться так, что каждая девочка знакома ровно с 3 из присутствующих на занятии кружковцев, а каждый мальчик ровно с 5? 7) Каждые две из шести ЭВМ соединены своим проводом. Можно ли раскрасить каждый из этих проводов в один из пяти цветов так, чтобы из каждой ЭВМ выходило пять проводов разного цвета? 8) В норке живёт семья из 24 мышей. Каждую ночь ровно четыре из них отправляются на склад за сыром. Может ли так получиться, что в некоторый момент времени каждая мышка побывала на складе с каждой ровно по одному разу? 9) Можно ли занумеровать ребра куба натуральными числами от 1 до 12 так, чтобы для каждой вершины куба сумма номеров ребер, которые в ней сходятся, была одинаковой? 3.1.9.Решите задачи по выявлению связности графа: 0) Можно ли соединить пять точек в связную систему так, чтобы при стирании любого отрезка образовались ровно две связные системы точек, не связанные друг с другом? (Мы считаем, что в местах пересечения отрезков переход с одного из них на другой невозможен.) 1) В Тридевятом царстве лишь один вид транспорта - ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний - одна, а из всех остальных городов - по 20. Докажите, что из столицы можно долететь в Дальний (возможно, с пересадками). 2) В стране из каждого города выходит 100 дорог и от любого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь эта возможность сохранилась. 3) Тетрадный лист раскрасили в 23 цвета по клеткам. Пара цветов называется хорошей, если существует две соседние клетки, закрашенные этими цветами. Каково минимальное число хороших пар? 4) В стране Древляндия 101 город, и некоторые из них соединены дорогами. При этом любые два города соединяет ровно один путь. Сколько в этой стране дорог? 5) Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля-Меркурий, Плутон-Венера, Земля-Плутон, Плутон-Меркурий, Меркурий-Венера, Уран-Нептун, Нептун-Сатурн, Сатурн-Юпитер, Юпитер-Марс и Марс-Уран. Можно ли добраться с Земли до Марса? 6) В стране Семерка 15 городов, каждый из которых соединен дорогами не менее, чем с 7 другими. Докажите, что из любого города можно добраться до любого другого (в т.ч., проезжая через другие города). 7) Гарри Поттер умеет превращать жабу в принцессу, гриб в жабу и грушу, грушу в яблоко, огрызок от яблока в котёнка и ёжика, котёнка в грушу или яблоко, ёжика в грушу, а яблоко — только в огрызок. Сейчас у него есть яблоко. Сможет ли он превратить его в принцессу? 8) В стране Цифра есть 9 городов с названиями от 1 до 9. Путешественник обнаружил, что два города соединены железной дорогой, если двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли добраться на поезде из города 1 в город 9? 9) Как соединить 50 городов наименьшим числом авиалиний так, чтобы из любого города можно было попасть в любой, сделав не более двух пересадок? Операции над графами Пусть даны два графа G1(V1, E1) и G2(V2, E2). Объединением графов G1(V1, E1) и G2(V2, E2) при условии, что V1ìüV2 = Æ; E1ìüE 2 = Æ, называется граф G1(V1, E1) îþ G2(V2, E2), множеством вершин которого является множество V1îþ V2, а множеством его ребер является множество E1îþE 2.
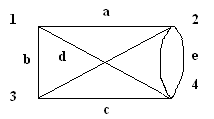
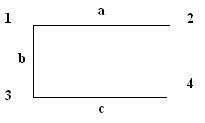
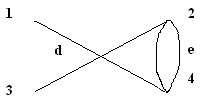
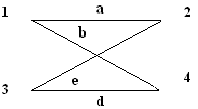
Пересечением графов G1(V1, E1) и G2(V2, E2) называется граф G1 (V1, E1) ìü G2 (V2, E2), множеством вершин которого является множество V1ìü V2, а множеством его ребер - множество E1ìüE 2. Суммой по модулю два графов G1(V1, E1) и G2(V2, E2) при условии, что V1ìüV2 = Æ; E1ìüE 2 = Æ, называется граф G1(V1, E1) Å G2(V2,E2), множеством вершин которого является множество V1îþ V2, а множеством его ребер - множество E1 Å E 2.. Этот граф состоит только из ребер, присутствующих либо в первом, либо во втором графе, но не в обоих одновременно. Дополнением графа G1 (V1, E1) называется граф Примеры выполнения заданий Пусть заданы два графа G1(V1, E1) и G2(V2, E2). Изобразите геометрически объединение, пересечение и сумму по модулю два.
Задания для самостоятельного выполнения 3.2.1. Пусть заданы два графа G1(V1, E1) и G2(V2, E2). Изобразите геометрически объединение, пересечение и сумму по модулю два.
Представление графов в ПЭВМ Неориентированные графы Неориентированный граф G (V, E) – непустое конечное множество узлов (вершин) V и набор неупорядоченных пар вершин (ребер) E. Способы задания графа: 1) аналитический (в виде алгебраической системы); 2) геометрический (в виде произвольного рисунка); 3) матричный (в виде матриц смежности и инцидентности). Пусть v 1, v 2,... vn - вершины графа G (V, E), а e 1, e 2,... em - его ребра. Матрицей смежности графа G называется матрица A(G)= || aij ||, i =1,..., n; Свойства матрицы смежности: 1) симметричная относительно главной диагонали, 2) значениями являются натуральные числа и ноль, 3) количество петель записывается на главной диагонали, 4) сумма значений по строке или в столбце равна валентности вершины.
Матрицей инцидентности для неориентированного графа с n вершинами и m ребрами называется матрица В(G) = [bij], i=1, 2,..., n, j = 1,2,..., m, строки которой соответствуют вершинам, а столбцы - ребрам. Элемент bij=1, если вершина vi инцидентна ребру ej и bij=0, если вершина vi не инцидентна ребру ej. Свойства матрицы инцидентности: 1) несимметричная, 2) значениями являются ноль и единица, 3) сумма значений по строке или в столбце равна 2, если нет петель. Примеры выполнения заданий
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 931; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.174 (0.013 с.) |



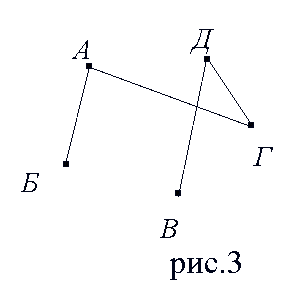
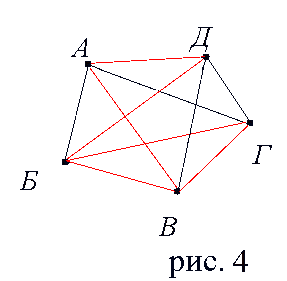
 множеством вершин которого является множество V1, а множеством его ребер является множество
множеством вершин которого является множество V1, а множеством его ребер является множество 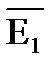 = {eÎ V1 x V1: eÏE1}
= {eÎ V1 x V1: eÏE1}