Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изобразите геометрически множество истинности двуместного предиката A(x, y).Содержание книги
Поиск на нашем сайте
Электронный практикум По дискретной математике для студентов факультета «Прикладная информатика» по областям
Глава 1. Элементы логики предикатов Понятие предиката Предикатом арности n (n-арным, или n-местным предикатом) называют функцию от n переменных Q(x1, x2, …,xn), определенную на декартовом произведении множеств: X1´X2´ …´Xn и принимающую значения из множества {И, Л}. Примеры выполнения заданий 1. Постройте матрицу одноместного предиката Р(x), если: P(x) = "x кратно 2", где xÎ [1, 14)
2. Изобразите геометрически множество истинности двуместного предиката P(x,y) = 1/4x ³ 1/4y”, если x, y Î (-2, 5];
область истинности предиката расположена ниже прямой, включая ее точки (т.к. нестрогое неравенство).
Задания для самостоятельного выполнения 1.1.1. Постройте матрицу одноместного предиката Q(x), если:
1.1.2. Изобразите геометрически множество истинности одноместных предикатов G(x) и P(x), если:
X 0 X 1.1.3. Изобразите геометрически множество истинности предиката P(x), решив систему неравенств:
X 0 1.1.4. Постройте матрицу двуместного предиката P(x,y) и проверьте решение геометрически:
Изобразите геометрически множество истинности двуместного предиката A(x, y).
Изобразите геометрически множество истинности двуместного предиката Q(x,y).
Операции над предикатами и кванторами Все логические операции логики высказываний справедливы и для предикатов (отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция). Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. В математической логике приписывание квантора к формуле называется связыванием, а переменную, к которой он относится, называют связанной иначе свободной. Например, в предикате "x A(x, y)Ú"z B(c, z) переменные x и z - связанные, а переменные у и z – свободные. Чаще всего используют два вида кванторов:
Пусть задан одноместный предикат P(x) на множестве Х = { a1, a2, a3, a4 }, тогда: "xP(x)=P(a1)&P(a2)&P(a3)&P(a4); $xP(x)=P(a1)ÚP(a2)ÚP(a3)ÚP(a4). Говорят, что у квантора всеобщности конъюнктивная природа, а у квантора существования – дизъюнктивная. Квантор уменьшает число свободных переменных в логическом выражении и превращает трёхместный предикат в двухместный, двухместный — в одноместный, одноместный — в высказывание. Примеры выполнения заданий 1. Пусть предикат Q(x,y) определен на конечных множествах: X={a1,a2,a3, a4, a5}, Y={b1, b2, b3, b4, b5, b6} и имеет таблицу истинности:
Глава 2. Комбинаторика
Размещения без повторений Размещениями из n элементов по m (m Задания для самостоятельного выполнения 0) Составьте все слова из трех букв А, В, С по две буквы. 1) В классе 30 учащихся. Сколькими способами можно выбрать из класса команду из 4 учащихся для участия в олимпиаде по истории? 2) Сколькими способами можно составить двуцветный полосатый флаг, если имеется материал 5 различных цветов? Та же задача, если одна из полос должна быть красной? 3) Из состава конференции, на которой присутствует 45 человека, надо избрать делегацию из 6 человек. Сколькими способами это можно сделать? 4) В турнире принимают участие 8 команд. Сколько различных предположений относительно распределения трех первых мест можно сделать? 5) Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различны и нечетны? 6) Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя 6 различных цветов? 7) Сколько существует трехзначных чисел, в записи которых цифры 1, 2, 3 встречаются ровно по одному разу? 8) На полке стоят 5 книг. Сколькими способами можно выложить в стопку несколько из них (стопка может состоять и из одной книги)? 9) У Димы есть 5 шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами он сможет украсить ими 5 елок, если на каждую требуется надеть ровно один шарик? Размещения с повторениями Размещениями с повторениями из n по m называются упорядоченные m-элементные выборки, в которых элементы могут повторяться. Задания для самостоятельного выполнения 0) Сколько четырехбуквенных «слов» можно составить из букв "М" и "А"? 1) Сколькими способами можно разместить восемь пассажиров в три вагона? 2) Каждый телефонный номер состоит из семи цифр. Сколько всего телефонных номеров, не содержащих других цифр, кроме 2, 3, 5 и 7? 3) Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки? 4) Сколько различных трехбуквенных слов можно составить из 32 букв алфавита (со смыслом и без)? 5) В селении проживает 2000 жителей. Доказать, что, по крайней мере, двое из них имеют одинаковые инициалы. 6) Сколькими способами можно покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски неограниченно, а каждую елку можно покрасить только в один цвет? 7) Каждую клетку квадратной таблицы 2 × 2 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы? 8) Сколькими способами можно заполнить одну карточку в лотерее «Спортпрогноз»'? Указание: в этой лотерее нужно предсказать итог тринадцати спортивных матчей. Итог каждого матча - победа одной из команд либо ничья; счет роли не играет. 9) Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке племени Мумбо-Юмбо? Указание: сосчитайте отдельно количества одно-, двух-, трех- и четырехбуквенных слов. Перестановки без повторений Перестановками из n элементов называются размещения из n элементов по n. Пусть (a1,a2,…,an), — перестановка элементов множества {1, 2,...,n}.Пара (ai, aj) называется инверсией перестановки, если i < j, то ai > aj. Таблицей инверсии перестановки (a1,a2,…,an) называется последовательность (d1,d2,…,dn),где dj — число элементов, больших j и расположенных левее j.
Задания для самостоятельного выполнения 0) Сколькими способами можно расставить 7 книг на книжной полке? 1) Сколькими способами можно разложить 8 различных писем по 8 различным конвертам, если в каждый конверт кладется только одно письмо? 2) Сколько ожерелий можно составить из семи бусин разных размеров? 3) Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом? 4) Сколько слов можно получить, переставляя буквы в слове «градус»? 5) Сколькими различными способами можно рассадить 6 человек на 6 креслах в кинотеатре? 6) Сколько всего шестизначных четных чисел можно составить из цифр 1, 3, 4, 5, 7 и 9, если из этих чисел ни одна не повторяется? 7) Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг друга? 8) Сколько всего семизначных четных чисел можно составить из цифр 0, 2, 3, 5, 7 и 9, если из этих чисел ни одна не повторяется? 9) Как велико число различных отображений, переводящих множество из n элементов в себя? Перестановки с повторениями Перестановки с повторениями вычисляются по формуле:
Задания для самостоятельного выполнения 0) Сколько различных шестизначных чисел можно составить из цифр: 1, 1, 1, 5, 5, 9? 1) Сколькими способами можно расположить в ряд 2 зеленые и 4 красные лампочки? 2) Сколько всего шестизначных чисел, у каждого из которых цифра 2 встречается два раза, а цифра 3 - четыре раза? 3) Имеется 5 мест на флагштоке и 5 флагов: 2 красных и 3 белых. Сколько можно изобразить различных сигналов, если использовать все флаги одновременно? 4) Сколько различных слов можно получить, переставляя буквы в слове «молоко»? В слове «караоке»? В слове «ингредиент»? 5) В магазине игрушек имеются 7 одинаковых Чебурашек и 2 одинаковых Крокодила. Сколькими способами их можно расставить в один ряд на витрине? 6) Сколькими способами можно разделить 40 одинаковых яблок а) между 4 мальчиками; в) чтобы каждый получил, по крайней мере, 3 яблока? 7) Сколькими способами в библиотеке можно расположить на одной полке 6 экземпляров романа «Овод», 7 экземпляров сказки «Золушка» и 8 экземпляров учебника Акимова «Дискретная математика»? 8) Сколькими способами можно расставить белые фигуры (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски? 9) В магазине ``Все для чая'' продается 7 чашек, 5 блюдец и 6 чайных ложек. Сколькими способами можно распределить посуду с разными названиями? Сочетания без повторений Сочетаниями из n элементов по m (m Задания для самостоятельного выполнения 0) Составьте все сочетания из трех букв А, В, С по две буквы. 1) У 6 взрослых и 11 детей обнаружены признаки инфекционного заболевания. Чтобы проверить заболевание, следует взять выборочный анализ у 2 взрослых и 3 детей. Сколькими способами можно это сделать? 2) Сколькими способами можно группу из 20 студентов разделить на две подгруппы так, чтобы в одной группе было 13, а в другой 7 человек? 3) На книжной полке стоят 3 книги по алгебре, 4 книги по геометрии и 5 книг по литературе. Сколькими способами можно взять с полки три книги по математике? 4) Учащийся хочет использовать для раскраски географической контурной карты 4 краски из 6, которые он имеет в своем распоряжении. Сколькими способами он может выбрать 4 краски из 6? 5) Даны две параллельные прямые. На одной из них имеется 10 точек, а на другой - 20. Сколько существует треугольников с вершинами в данных точках? 6) Сколькими способами можно распределить 28 костей домино между 4 игроками так, чтобы каждый получил 7 костей? 7) В классе 12 юношей и 13 девушек. Сколькими способами из них можно выбрать четырех учащихся для дежурства на вечере, если а) освободить девушек; б) юноши и девушки? 8) Сколькими способами абитуриент может выбрать 3 ВУЗа из 5 для подачи документов? 9) Из двух математиков и десяти экономистов надо составить комиссию в составе восьми человек. Сколькими способами может быть составлена комиссия, если в нее должен входить хотя бы один математик?
Сочетания с повторениями Сочетаниями с повторениями из n по m называются неупорядоченные m-элементные выборки, в которых элементы могут повторяться.
Задания для самостоятельного выполнения 0) В почтовом отделении имеются открытки 3 видов. Сколькими способами можно купить набор из 6 открыток? 1) Сколькими способами можно выбрать четыре из четырех пятикопеечных монет и из четырех двухкопеечных монет? 2) В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 8 булок хлеба? 3) Сколько имеется костей в обычной игре "домино"? 4) Сколько вариантов строения ДНК Шубуршунчика обворожительного может быть, если длина цепи 1000 нуклеотидов (нуклеотиды 4 видов: А, Т, Г, Ц)? 5) Сколько всего чисел можно составить из цифр 1, 2, 3, 4, 5, в каждом из которых цифры расположены в неубывающем порядке? 6) Шесть пассажиров садятся на остановке в трамвайный поезд, состоящий из трех трамвайных вагонов. Сколькими различными способами могут они распределиться в каждом из 3 вагонов? 7) Как велико число отличных друг от друга результатов бросаний двух одинаковых кубиков? 8) Сколькими способами можно выбрать 7 крупных апельсинов из 2 имеющихся на рынке сортов? 9) В магазине продаются белые, черные и красные носки. Сколькими способами можно купить 5 пар?
Примеры решения сложных задач Приведем в систему полученные формулы всех 6 видов комбинаций с повторениями и без повторений, представив алгоритм определения вида комбинации (см. рис. 1). Задания для самостоятельного выполнения 0) Из 10 роз и 8 георгинов нужно составить букет так, чтобы в нем было 2 розы и 3 георгина. Сколькими способами это можно сделать? 1) Собрание из 40 человек избирает председателя, секретаря и трех членов редакционной комиссии. Сколько существует возможностей выбора этих пяти человек? 2) Сколькими способами можно расставить 8 томов энциклопедии на книжной полке так, чтобы первый и второй тома: а) стояли рядом; б) не стояли рядом? 3) На окружности расположено 20 точек. Сколько существует вписанных треугольников с вершинами в этих точках? 4) Сколько существует номерных знаков для автомобилей, состоящих из двух букв с последующими четырьмя цифрами, если буквы могут повторяться, а цифры — нет? 5) Лифт, в котором находится восемь пассажиров, останавливается на шести этажах. Пассажиры выходят группами по одному, три и четыре человека. Сколькими способами это может произойти, если на каждом этаже может выйти только одна группа пассажиров, при этом порядок выхода пассажиров одной группы не имеет значения? 6) В алфавите племени Бум-Бум шесть букв. Словом является любая последовательность из шести букв, в которой есть хотя бы две одинаковые буквы. Сколько слов в языке племени Бум-Бум? 7) В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране? 8) На глобусе проведены 17 параллелей и 24 меридиана. На сколько частей разделена поверхность глобуса? Меридиан — это дуга, соединяющая Северный полюс с Южным. Параллель — это окружность, параллельная экватору (экватор тоже является параллелью). Указание. Решите задачу для двух меридианов (0o и 180o) и одной параллели (экватора). 9) У людоеда в подвале томятся 25 пленников. а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин? б) Сколько есть способов выбрать 3-х, чтобы отпустить на свободу?
Рис. 1. Алгоритм определения вида комбинации Задание 1. 0) Из города А в город В ведут пять дорог, а из города В в город С – три дороги. Сколько путей, проходящих через В, ведут из А в С? 1) Из двух спортивных обществ, насчитывающих по 100 фехтовальщиков каждое, надо выделить по одному фехтовальщику для участия в состязании. Сколькими способами может быть сделан этот выбор? 2) Имеется пять видов конвертов без марок и четыре вида марок одного достоинства. Сколькими способами можно выбрать конверт с маркой для посылки письма? 3) Сколькими способами можно выбрать гласную и согласную буквы из слова «камзол»? 4) Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»? 5) Бросают игральную кость с шестью гранями и запускают волчок, имеющий восемь граней. Сколькими различными способами они могут упасть? 6) На вершину горы ведут пять дорог. Сколькими способами •турист может подняться на гору и спуститься с нее? То же самое при условии, что спуск и подъем происходят по разным путям. 7) На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз? 8) Сколькими способами можно указать на шахматной доске два квадрата – белый и черный? А если нет ограничений на цвет выбранных квадратов? 9) Из 12 слов мужского рода, 9 женского и 10 среднего надо выбрать по одному слову каждого рода. Сколькими способами может быть сделан этот выбор? Задание 2. 0) В местком избрано 9 человек. Из них надо выбрать председателя, заместителя председателя, секретаря и культорга. Сколькими способами это можно сделать? 1) Из состава конференции, на которой присутствует 52 человека, надо избрать делегацию, состоящую из 5 человек. Сколькими способами это можно сделать? 2) Автомобильные номера состоят из одной, двух или трех букв и четырех цифр. Найти число таких номеров, если используются 32 буквы русского алфавита. 3) Сколько различных перестановок можно получить, переставляя буквы в слове «математика»? В слове «парабола»? 4) В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? Сколькими способами можно купить 8 открыток? 5) Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них' было не менее 2 женщин. Сколькими способами это можно сделать? 6) Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки? 7) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз? 8) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно один туз? 9) Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно два туза?
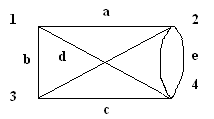
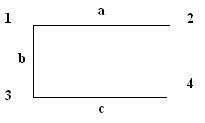
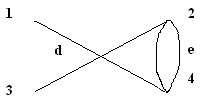
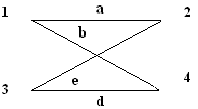
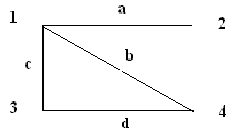
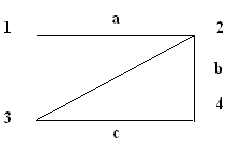
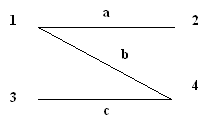
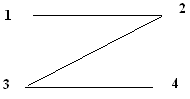
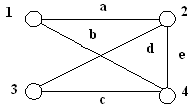
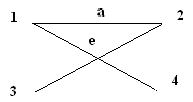
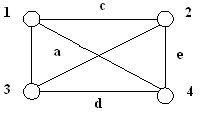
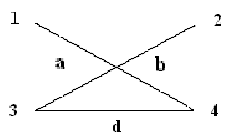
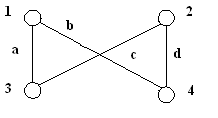
Глава 3. Графы Операции над графами Пусть даны два графа G1(V1, E1) и G2(V2, E2). Объединением графов G1(V1, E1) и G2(V2, E2) при условии, что V1ìüV2 = Æ; E1ìüE 2 = Æ, называется граф G1(V1, E1) îþ G2(V2, E2), множеством вершин которого является множество V1îþ V2, а множеством его ребер является множество E1îþE 2. Пересечением графов G1(V1, E1) и G2(V2, E2) называется граф G1 (V1, E1) ìü G2 (V2, E2), множеством вершин которого является множество V1ìü V2, а множеством его ребер - множество E1ìüE 2. Суммой по модулю два графов G1(V1, E1) и G2(V2, E2) при условии, что V1ìüV2 = Æ; E1ìüE 2 = Æ, называется граф G1(V1, E1) Å G2(V2,E2), множеством вершин которого является множество V1îþ V2, а множеством его ребер - множество E1 Å E 2.. Этот граф состоит только из ребер, присутствующих либо в первом, либо во втором графе, но не в обоих одновременно. Дополнением графа G1 (V1, E1) называется граф Примеры выполнения заданий Пусть заданы два графа G1(V1, E1) и G2(V2, E2). Изобразите геометрически объединение, пересечение и сумму по модулю два.
Задания для самостоятельного выполнения 3.2.1. Пусть заданы два графа G1(V1, E1) и G2(V2, E2). Изобразите геометрически объединение, пересечение и сумму по модулю два.
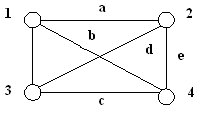
Представление графов в ПЭВМ Неориентированные графы Неориентированный граф G (V, E) – непустое конечное множество узлов (вершин) V и набор неупорядоченных пар вершин (ребер) E. Способы задания графа: 1) аналитический (в виде алгебраической системы); 2) геометрический (в виде произвольного рисунка); 3) матричный (в виде матриц смежности и инцидентности). Пусть v 1, v 2,... vn - вершины графа G (V, E), а e 1, e 2,... em - его ребра. Матрицей смежности графа G называется матрица A(G)= || aij ||, i =1,..., n; Свойства матрицы смежности: 1) симметричная относительно главной диагонали, 2) значениями являются натуральные числа и ноль, 3) количество петель записывается на главной диагонали, 4) сумма значений по строке или в столбце равна валентности вершины. Матрицей инцидентности для неориентированного графа с n вершинами и m ребрами называется матрица В(G) = [bij], i=1, 2,..., n, j = 1,2,..., m, строки которой соответствуют вершинам, а столбцы - ребрам. Элемент bij=1, если вершина vi инцидентна ребру ej и bij=0, если вершина vi не инцидентна ребру ej. Свойства матрицы инцидентности: 1) несимметричная, 2) значениями являются ноль и единица, 3) сумма значений по строке или в столбце равна 2, если нет петель. Примеры выполн |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 989; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

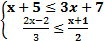
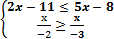
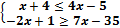
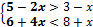
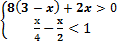
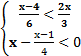
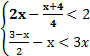
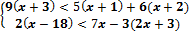
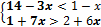
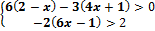
 n) называются упорядоченные m -элементные выборки из данных n элементов
n) называются упорядоченные m -элементные выборки из данных n элементов 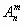 .
. 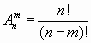

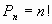
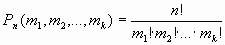

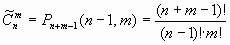

 множеством вершин которого является множество V1, а множеством его ребер является множество
множеством вершин которого является множество V1, а множеством его ребер является множество 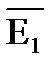 = {eÎ V1 x V1: eÏE1}
= {eÎ V1 x V1: eÏE1}