
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граф G(V,E): задан геометрически.Содержание книги
Поиск на нашем сайте
а) Задайте граф G(V,E) как алгебраическую систему. б) Выясните, является ли заданное отношение отношением эквивалентности
Решение: а)V={1,2,3,4,}, E={(1,1),(1,2),(2.2),(2,1),(3,3),(3,4),(4,3),(1,4),(4,4),(4,1),(4,5),(5,4),(5,5) б) Нарушено условие транзитивности. Отсутствуют пары (2,4), (4,2), (2,3), (3,2), (3,5),(5,3), (2,5), (5,2), (1,5), (5,1), поэтому отношение R не является эквивалентным. 3. Графы G1(V1,E1) и G2(V2,E2) заданы геометрически. Постройте: а) для графа G1(V1,E1) матрицу смежности, б) для графа G2(V2,E2) матрицу смежности и матрицу инцидентности.
Задания для самостоятельного выполнения 3.3.1.1. Граф G(V,E): V={a, b, c, d, e}, задан как алгебраическая система. a) Для приведенного отношения задайте граф геометрически. б) Выясните, является ли заданное отношение отношением эквивалентности. 0) R = {(a, a), (а, b), (b, а), (b, b), (b, с), (с, b), (с, а), (а, с), (d, e), (е, d), (d, d)}; 1) R = {(а, 6), (b, a), (b, b), (b, с), (с, b), (с, d), (d, с), (с, а), (а, с), (c, c), (d, d)}; 2) R = {(b, b), (b, а), (b, с), (с, b), (c, c), (с, d), (d, с), (d, e), (e, d), (a, a), (e, e)}; 3) R = {(a, b), (a, а), (b, с), (b, b), (c, c), (d, d), (d, с), (d, e), (e, e), (a, e), (e, a)}; 4) R = {(b, c), (b, а), (b, d), (с, b), (c, a), (с, d), (d, с), (d, a), (e, d), (a, b), (d, d)}; 5) R = {(b, b), (a, а), (c, с), (с, b), (b, c), (с, d), (d, с), (d, d), (e, d), (d, e), (e, e)}; 6) R = {(a, c), (b, c), (c, с), (с, b), (c, a), (с, d), (d, с), (d, e), (d, d), (a, a), (e, a)}; 7) R = {(b, b), (a, а), (c, с), (d, b), (b, d), (d, d), (d, с), (d, e), (d, a), (a, c), (e, c)}; 8) R = {(e, d), (d, а), (a, b), (с, b), (e, c), (с, e), (e, a), (b, e), (e, e), (a, e), (c, c)}; 9) R = {(c, b), (b, c), (b, a), (a, b), (c, c), (с, d), (e, с), (d, e), (e, d), (a, a), (e, e)}. Постройте для графа G(V,E), заданного геометрически а) матрицу смежности; б) матрицу инциденций.
3.
Матрицу смежности и матрицу инцидентности. Задайте граф как алгебраическую систему. Подсчитайте валентность вершин. Определите тип графа.
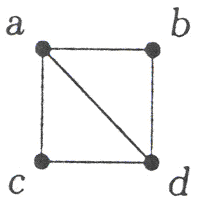 

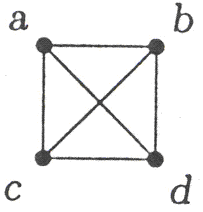
Ориентированные графы Ориентированный граф (или орграф) G1 (V, E) – непустое конечное множество узлов (вершин) V и набор упорядоченных пар вершин (дуг) E. Пусть v 1, v 2,... vn - вершины графа G1 (V, E), а e 1, e 2,... em - его дуги. Матрицей смежности графа G1 называется матрица A(G1)= || aij ||, i =1,..., n; Свойства матрицы смежности: 1) несимметричная, в общем случае, относительно главной диагонали, 2) значениями являются натуральные числа и ноль, 3) количество петель записывается на главной диагонали, 4) сумма значений по строке (столбце) равна валентности вершины. Матрицей инцидентности для ориентированного графа с n вершинами и m дугами называется матрица В(G1) = [bij], i=1, 2,..., n, j = 1,2,..., m, строки которой соответствуют вершинам, а столбцы - дугам. Ее элемент: bij=1, если дуга еi выходит из вершины vj; bij= -1, если дуга ei входит в вершины vj; bij=0, если вершина vj не инцидентна дуге еi. Свойства матрицы инцидентности: 1) несимметричная, 2) значениями являются -1, ноль и 1. Примеры выполнения заданий 1. Орграф G1(V,E) задан геометрически. Постройте для орграфа: а) матрицу смежности; б) матрицу инцидентности.
2. Решите следующую задачу по обходу графов: В некоторой стране есть столица и еще 100 городов. Некоторые города (в том числе и столица) соединены дорогами с односторонним движением. Из каждого нестоличного города выходит 20 дорог, и в каждый такой город входит 21 дорога. Докажите, что в столицу нельзя проехать ни из одного города. Решение: Пусть в столицу входит a дорог. Тогда общее число "входящих" дорог равно 21 · 100 + a, а общее количество "выходящих" дорог не больше 20 · 100 + (100- a). Поэтому 21×100 + а £ 20×100 + (100 – а), то есть 2а £ 0. Таким образом, a = 0. Задания для самостоятельного выполнения 3.3.2.1. Орграф G1(V,E): V={a, b, c, d, e, f}, задан как алгебраическая система. a) Для приведенного отношения задайте орграф геометрически. б) Постройте матрицу смежности орграфа. 0) R = {(а, b), (b, а), (b, с), (с, b), (с, а), (а, с), (d, e), (е, d)}; 1) R = {(а, b), (b, a), (b, с), (с, b), (с, d), (d, с), (с, а), (а, с)}; 2) R = {(a, b), (b, а), (b, с), (с, b), (с, d), (d, с), (d, e), (e, d)}; 3) R = {(а, b), (b, с), (а, с), (b, е), (с, f), (с, d), (d, f), (f, е)}; 4) R = {(b, c), (a, d), (b, a), (d, c), (b, d), (с, a), (f, d), (f,c)}; 5) R = {(b, а), (а, а), (b, с), (с, d), (d, с), (d, b), (d, а), (d, e)}; 6) R = {(a, b), (а, с), (а, d), (с, а), (d, e), (e, d), (c, c), (d, b)}; 7) R={(b, a), (c, с), (а, d), (с, а), (d, e), (e, c), (d, b), (e, f)}; 8) R = {(a, b), (а, с), (а, d), (e, а), (d, e), (e, d), (c, b), (d, d)}; 9) R = {(a, e), (а, a), (а, d), (с, а), (d, e), (d, d), (c, c), (b, d)}.
3.3.2.2. Орграф задан геометрически. Укажите валентность вершин.Постройте матрицу смежности орграфа.
3.3.2.3. Дана матрица смежности орграфа. а) Задайте орграф геометрически, в) постройте матрицу инцидентности. 0) 5) 3.3.2.4. Дана матрица инцидентности орграфа. а) Задайте орграф геометрически, в) постройте матрицу смежности.
3.3.2.5. Решите следующие задачи по обходу графов: 0) Дима, приехав из Врунляндии, рассказал, что там есть несколько озер, соединенных между собой реками. Из каждого озера вытекают три реки, и в каждое озеро впадают четыре реки. Докажите, что он ошибается. 1) В некотором государстве каждый город соединен с каждым дорогой. Сумасшедший король хочет ввести на дорогах одностороннее движение так, чтобы, выехав из любого города, в него нельзя было вернуться. Можно ли так сделать? 2) Утверждают, что в одной компании из пяти человек каждый знаком с двумя другими. Возможна ли такая компания? 3) В некотором государстве 101 город. Все города соединены дорогами с односторонним движением, причем в каждый город входит 50 дорог и из каждого города выходит 50 дорог. Докажите, что из любого города можно доехать в любой другой, проехав не более, чем по двум дорогам. 4) На плоскости даны 6 точек так, что никакие три из них не лежат на одной прямой. Каждая пара точек соединена отрезком синего или красного цвета. Докажите, что среди данных точек можно выбрать такие три, что все стороны образованного ими треугольника будут окрашены в один цвет. 5) В некотором государстве 101 город. Некоторые города соединены дорогами с односторонним движением, причем в каждый город входит 40 дорог и из каждого города выходит 40 дорог. Докажите, что из любого города можно добраться до любого другого, проехав не более, чем по трем дорогам. 6) Можно ли провести в городе 10 автобусных маршрутов и установить на них остановки так, что какие бы 8 маршрутов ни были взяты, найдётся остановка, не лежащая ни на одном из них, а любые 9 маршрутов проходят через все остановки. 7) Жук ползет по ребрам куба. Сможет ли он последовательно обойти все ребра, проходя по каждому ребру ровно один раз? Указание: задумайтесь над вопросом: сколько раз жук может побывать в каждой вершине? 8) Художник нарисовал картину "Контур квадрата и его диагонали". Мог ли он нарисовать свою картину, не отрывая карандаша от бумаги и не проводя одну линию дважды? Указание: из каждой точки, за исключением начала и конца пути карандаша, должно исходить четное число линий. 9) Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
3.3.2.6. Решите следующие задачи по обходу графов: 0) Метро города Урюпинска состоит из трёх линий и имеет, по крайней мере, две конечные станции и, по крайней мере, два пересадочных узла, причём ни одна из конечных станций не является пересадочной. С каждой линии на каждую можно перейти, по крайней мере, в двух местах. Нарисуйте пример такой схемы метро, если известно, что это можно сделать, не отрывая карандаша от бумаги и не проводя два раза один и тот же отрезок. Указание: не забудьте, что бывают кольцевые линии. 1) Как, не отрывая карандаша от бумаги, провести шесть отрезков таким образом, чтобы оказались зачёркнутыми 16 точек, расположенных в вершинах квадратной сетки 4 на 4? 2) Можно ли провести в каждом квадратике на поверхности кубика Рубика диагональ так, чтобы получился несамопересекающийся путь? 3) Доска имеет форму креста, который получается, если из квадратной доски 4 × 4 выкинуть угловые клетки. Можно ли обойти ее ходом шахматного коня и вернуться на исходное поле, побывав на всех полях ровно по разу? 4) Пешеход обошёл шесть улиц одного города, пройдя каждую ровно два раза, но не смог обойти их, пройдя каждую лишь раз. Могло ли это быть? 5) В центре куба 3´3´3 сидит жук. Доказать, что он, переползая через ребра, не сможет обойти все кубики 1´1´1по одному разу. 6) В квадрате 6×6 отмечают несколько клеток так, что из любой отмеченной можно пройти в любую другую отмеченную, переходя только через общие стороны отмеченных клеток. Отмеченную клетку называют концевой, если она граничит по стороне ровно с одной отмеченной. Отметьте несколько клеток так, чтобы получилось а) 10, б) 11, в) 12 клеток. 7) В одной из вершин а) октаэдра б) куба сидит муха. Может ли она проползти по всем его ребрам ровно по одному разу и возвратиться в исходную вершину? (Примечание: октаэдр представляет собой две четырехугольные пирамиды, склеенные по основаниям.) 8) Как, не отрывая карандаша от бумаги, провести шесть отрезков таким образом, чтобы оказались зачёркнутыми 16 точек, расположенных в вершинах квадратной сетки 4 на 4? 9) Можно ли провести в каждом квадратике на поверхности кубика Рубика диагональ так, чтобы получился несамопересекающийся путь? Указание: на поверхности кубика Рубика всего 54 квадрата.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.74.47 (0.008 с.) |

 Решение:
Матрица смежности:
v1 v2 v3 v4
А(G) =
Решение:
Матрица смежности:
v1 v2 v3 v4
А(G) = 
 В(G) =
В(G) = 







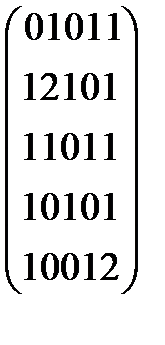

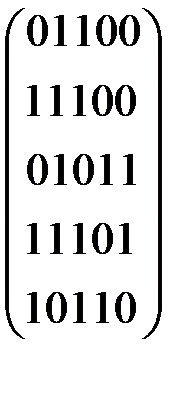
 1)
1)  2)
2)  3)
3)  4)
4) 
 6)
6)  7)
7)  8)
8)  9)
9) 



