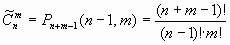Инверсии. Обратные перестановки

Пусть (a1,a2,…,an), — перестановка элементов множества {1, 2,...,n}.Пара (ai,aj) называется инверсией перестановки, если i<j, а ai>aj.

Например, перестановка (3 1 4 2) имеет три инверсии (3, 1), (3, 2), (4, 2).

Каждая инверсия — это пара элементов, «нарушающих порядок», следовательно, единственная перестановка, не содержащая инверсий, отсортированная перестановка (1, 2,..., n).

Таблицей инверсии перестановки (a1,a2,…,an),называется последовательность (d1,d2,…,dn),где dj — число элементов, больших j и расположенных левее j. То есть dj— число инверсий, у которых второй элемент равен j.

Задания для самостоятельного выполнения

2.6.1. Составьте таблицу инверсий для перестановки:
0) b= {5,7,3,4,2,6,1,10,11,8,9}; 1) b= {7,4,3,1,5,6,2,8,11,10,9}; 2) b= {3,2,1,4,5,10,7,11,9,6,8}; 3) b= {10,11,8,7,5,6,4,3,9,1,2}; 4) b= {4,5,3,1,2,8,7,6,9,11,10};	5) b= {11,2,9,8,5,6,7,4,3,10,1}; 6) b= {6,10,3,4,5,1,8,7,9,2,11}; 7) b= {8,9,5,4,3,6,7,1,2,10,11}; 8) b= {9,7,10,4,11,6,2,8,1,3,5}; 9) b= {4,7,6,9,11,10,5,8,3,1,2}.
2.6.2. Составьте перестановку по заданной таблице инверсий:
0) d = {8,6,7,3,6,4,1,3,0,0,0}; 1) d = {7,7,4,2,2,2,2,0,0,0,0}; 2) d = {5,1,7,6,2,0,2,1,1,0,0}; 3) d = {10,1,7,6,3,3,3,2,1,1,0}; 4) d = {3,3,2,0,0,2,1,0,0,1,0};	5) d = {9,9,7,6,4,4,3,2,2,0,0}; 6) d = {2,1,0,0,0,4,1,3,2,0,0}; 7) d = {3,5,2,1,1,1,0,0,2,1,0}; 8) d = {6,4,2,2,0,0,0,2,2,0,0}; 9) d = {4,2,6,5,1,2,8,9,2,3,0}.
2.6.3. Составьте обратную перестановку a ^–1 для заданной перестановки a и вычислите: a a ^–1:
0) A = {5,7,3,4,2,6,1,10,11,8,9}; 1) A = {7,4,3,1,5,6,2,8,11,10,9}; 2) A = {3,2,1,4,5,10,7,11,9,6,8}; 3) A = {10,11,8,7,5,6,4,3,9,1,2}; 4) A = {4,5,3,1,2,8,7,6,9,11,10};	5) A = {11,2,9,8,5,6,7,4,3,10,1}; 6) A = {6,10,3,4,5,1,8,7,9,2,11}; 7) A = {8,9,5,4,3,6,7,1,2,10,11}; 8) A = {9,7,10,4,11,6,2,8,1,3,5}; 9) A = {4,7,6,9,11,10,5,8,3,1,2}.
2.6.4. Найдите перестановку c = ab, если:
0) A = {11,2,9,8,5,6,7,4,3,10,1}; b={7,4,3,1,5,6,2,8,11,10,9}; 1) A = {6,10,3,4,5,1,8,7,9,2,11}; b={7,4,3,1,5,6,2,8,11,10,9}; 2) A = {8,9,5,4,3,6,7,1,2,10,11}; b={7,4,3,1,5,6,2,8,11,10,9}; 3) A = {9,7,10,4,11,6,2,8,1,3,5}; b={5,7,3,4,2,6,1,10,11,8,9}; 4) A = {4,7,6,9,11,10,5,8,3,1,2}; b={3,2,1,4,5,10,7,11,9,6,8}.	5) a = {5,7,3,4,2,6,1,10,11,8,9}; b={7,4,3,1,5,6,2,8,11,10,9}; 6) A = {7,4,3,1,5,6,2,8,11,10,9}; b={4,7,6,9,11,10,5,8,3,1,2}; 7) A = {3,2,1,4,5,10,7,11,9,6,8}; b={9,7,10,4,11,6,2,8,1,3,}; 8) A = {10,11,8,7,5,6,4,3,9,1,2}; b={8,9,5,4,3,6,7,1,2,10,11}; 9) A = {4,5,3,1,2,8,7,6,9,11,10}; b={6,10,3,4,5,1,8,7,9,2,11};

Сочетания без повторений

Сочетаниями из n элементов по m (m n) называются неупорядоченные m-элементные выборки из данных n элементов.

Задания для самостоятельного выполнения

0) Составьте все сочетания из трех букв А, В, С по две буквы.

1) У 6 взрослых и 11 детей обнаружены признаки инфекционного заболевания. Чтобы проверить заболевание, следует взять выборочный анализ у 2 взрослых и 3 детей. Сколькими способами можно это сделать?

2) Сколькими способами можно группу из 20 студентов разделить на две подгруппы так, чтобы в одной группе было 13, а в другой 7 человек?

3) На книжной полке стоят 3 книги по алгебре, 4 книги по геометрии и 5 книг по литературе. Сколькими способами можно взять с полки три книги по математике?

4) Учащийся хочет использовать для раскраски географической контурной карты 4 краски из 6, которые он имеет в своем распоряжении. Сколькими способами он может выбрать 4 краски из 6?

5) Даны две параллельные прямые. На одной из них имеется 10 точек, а на другой - 20. Сколько существует треугольников с вершинами в данных точках?

6) Сколькими способами можно распределить 28 костей домино между 4 игроками так, чтобы каждый получил 7 костей?

7) В классе 12 юношей и 13 девушек. Сколькими способами из них можно выбрать четырех учащихся для дежурства на вечере, если а) освободить девушек; б) юноши и девушки?

8) Сколькими способами абитуриент может выбрать 3 ВУЗа из 5 для подачи документов?

9) Из двух математиков и десяти экономистов надо составить комиссию в составе восьми человек. Сколькими способами может быть составлена комиссия, если в нее должен входить хотя бы один математик?

 

Сочетания с повторениями

Сочетаниями с повторениями из n по m называются неупорядоченные m-элементные выборки, в которых элементы могут повторяться.

Задания для самостоятельного выполнения

0) В почтовом отделении имеются открытки 3 видов. Сколькими способами можно купить набор из 6 открыток?

1) Сколькими способами можно выбрать четыре из четырех пятикопеечных монет и из четырех двухкопеечных монет?

2) В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 8 булок хлеба?

3) Сколько имеется костей в обычной игре "домино"?

4) Сколько вариантов строения ДНК Шубуршунчика обворожительного может быть, если длина цепи 1000 нуклеотидов (нуклеотиды 4 видов: А, Т, Г, Ц)?

5) Сколько всего чисел можно составить из цифр 1, 2, 3, 4, 5, в каждом из которых цифры расположены в неубывающем порядке?

6) Шесть пассажиров садятся на остановке в трамвайный поезд, состоящий из трех трамвайных вагонов. Сколькими различными способами могут они распределиться в каждом из 3 вагонов?

7) Как велико число отличных друг от друга результатов бросаний двух одинаковых кубиков?

8) Сколькими способами можно выбрать 7 крупных апельсинов из 2 имеющихся на рынке сортов?

9) В магазине продаются белые, черные и красные носки. Сколькими способами можно купить 5 пар?

 

Примеры решения сложных задач

Приведем в систему полученные формулы всех 6 видов комбинаций с повторениями и без повторений, представив алгоритм определения вида комбинации (см. рис. 1).

Задания для самостоятельного выполнения

0) Из 10 роз и 8 георгинов нужно составить букет так, чтобы в нем было 2 розы и 3 георгина. Сколькими способами это можно сделать?

1) Собрание из 40 человек избирает председателя, секретаря и трех членов редакционной комиссии. Сколько существует возможностей выбора этих пяти человек?

2) Сколькими способами можно расставить 8 томов энциклопедии на книжной полке так, чтобы первый и второй тома:

а) стояли рядом; б) не стояли рядом?

3) На окружности расположено 20 точек. Сколько существует вписанных треугольников с вершинами в этих точках?

4) Сколько существует номерных знаков для автомобилей, состоящих из двух букв с последующими четырьмя цифрами, если буквы могут повторяться, а цифры — нет?

5) Лифт, в котором находится восемь пассажиров, останавливается на шести этажах. Пассажиры выходят группами по одному, три и четыре человека. Сколькими способами это может произойти, если на каждом этаже может выйти только одна группа пассажиров, при этом порядок выхода пассажиров одной группы не имеет значения?

6) В алфавите племени Бум-Бум шесть букв. Словом является любая последовательность из шести букв, в которой есть хотя бы две одинаковые буквы. Сколько слов в языке племени Бум-Бум?

7) В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?

8) На глобусе проведены 17 параллелей и 24 меридиана. На сколько частей разделена поверхность глобуса? Меридиан — это дуга, соединяющая Северный полюс с Южным. Параллель — это окружность, параллельная экватору (экватор тоже является параллелью).

Указание. Решите задачу для двух меридианов (0^o и 180^o) и одной параллели (экватора).

9) У людоеда в подвале томятся 25 пленников.

а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин? б) Сколько есть способов выбрать 3-х, чтобы отпустить на свободу?

 

 

Рис. 1. Алгоритм определения вида комбинации