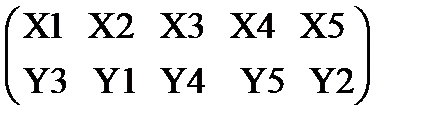Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды графов. Изоморфизм графов.Содержание книги
Поиск на нашем сайте Любая система, предполагающая наличие дискретных состояний или наличие узлов и переходов между ними может быть описана графом. Соединения между узлами (V) графа называются ребрами (E). Если узлы графа не нумерованы, то ребра являются неориентированными. У графа с нумерованными узлами ребра ориентированы и называются дугами
Число ребер, исходящих из вершины vi(петля учитывается дважды), называется валентностью (степенью вершины) и обозначается:d(vi). Если V и E конечные множества, то и граф им соответствующий называется конечным. Граф называется вырожденным, если он не имеет ребер. Неориентированный граф называется простым, если он не имеет петель и любая пара вершин соединена не более чем одним ребром. Графы отображаются на плоскости набором точек и соединяющих их линий или векторов. Грани могут отображаться и кривыми линиями, а их длина не играет никакой роли. Граф G называется планарным (плоским), если его можно отобразить в плоскости без пересечения его граней (рис. 5). Граф называется связным, если для любых двух вершин существует последовательность ребер их соединяющая (рис. 3), т.е. граф не имеет изолированных фрагментов (вершин, ребер). Граф называется полным, если любые две вершины соединены только одним ребром (рис.4). Если полный граф имеет n вершин, то количество ребер будет равно n(n-1)/2. Специальными видами графов являются деревья (рис. 6), кольца и списки, что не входит в рассмотрение нашего курса. Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом.
Часто на одном множестве объектов определено несколько различных бинарных отношений. Для представления такой ситуации служат мультиграфы. Мультиграфы будут использоваться для представления диаграмм конечных автоматов. Ребро (дуга) и любая из его вершин называются инцидентными. Принято говорить, что (дуга) ребро (u, v) соединяет вершины u и v. Если вершина не инцидентна ни одному ребру (дуге), то она называется изолированной (d(vi)=0), если принадлежит только одному ребру (дуге), то называется висячей (d(vi)=1). Основные положения о вершинах графа: 1. В графе G сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа, так как каждое ребро участвует в этой сумме ровно два раза. Этот результат называют леммой о рукопожатиях: если несколько человек обменялись рукопожатиями, то общее число пожатых рук обязательно четно, ибо в каждом рукопожатии участвуют две руки (при этом каждая рука считается столько раз, сколько она участвовала в рукопожатиях). 2. Число нечетных вершин любого графа четно. 3. Во всяком графе с n вершинами, где n ³2, всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями. 4. Если в графе с вершинами n>2 две вершины имеют одинаковую степень, то в этом графе всегда найдется либо одна вершина степени 0, либо одна вершина степени n - 1. Два графа G1=(V1,E1) и G2=(V2,E2) называются изоморфными, если между их вершинами существует взаимно однозначное соответствие. Алгоритм распознавания изоморфизма двух графов G1(X, E)и G2(Y,E) 1. Если X ≠ Y, то графы не изоморфны. 2. Выписываем все элементы обоих графов, определяя пары (xi,xj) и (yi, yj) для каждого элемента, где xi, yi - число исходов для каждой вершины обоих графов, а xj, yj – число заходов. 3. Для каждого элемента x графа G1 ищем такой элемент y графа G2, что выполняется условие: число исходов x совпадает с числом исходов y, и число заходов x совпадает с числом заходов y. Найденные элементы x и y соединяем дугой, т.е. строим граф соответствия. Если соответствия нет, то графы неизоморфны. 4. Выписываем подстановку, которая переводит граф G1 в граф G2.
Примеры выполнения заданий 1. 
А Б Решение: А) d(v1)=2,d(v2)=3,d(v3)=3,d(v4)=2,d(v5)=3,d(v6)=3. Б) d(v1)=2,d(v2)=3,d(v3)=3,d(v4)=2,d(v5)=3,d(v6)=3. 2. Докажите, что графы G1(X1, E1) и G2(Y2, E2) изоморфны.
Решение:
В результате получим подстановку:
Следовательно, графы G1(X, E) и G2(Y, E)изоморфны.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 816; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.009 с.) |

 Рис. 2. Примеры А) неориентированного и Б) ориентированного графов.
Рис. 2. Примеры А) неориентированного и Б) ориентированного графов.
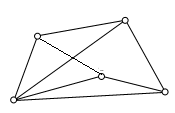 Рис. 5. Пример непланарного графа
Рис. 5. Пример непланарного графа