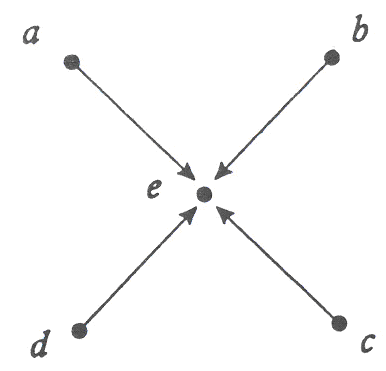
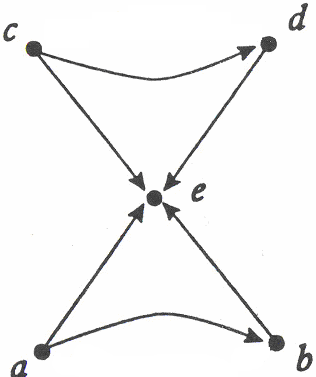
Орграф задан геометрически. Постройте матрицу расстояний.

Вычислите центр орграфа.

2)

3)

4)

5)

6)

7)

0)

1)

8)

9)

0)

 

 

3.4.3.Определите кратчайший путь от вершины графа, отмеченной номером варианта до вершины А.

 

 

7)

3.4.4. Дано множество пунктов А={1,2,3,4,5,6,7,8}. Построить граф самой экономичной сети дорог, если прокладка дорог (1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8), (2,3), (2,4), (2,5), (2,6), (2,7), (2,8), (3,4), (3,5), (3,6), (3,7), (3,8), (4,5), (4,6), (4,7), (4,8), (5,6), (5,7), (5,8), (6,7), (6,8), (7,8) имеет соответственно стоимости, заданные множеством:

0) А={10,11,9,8,9,15,5,12,7,14,8,10,2,6,7,18,3,21,12,14,3,6,23,3,4,8,6,9}

1) А={12,10,9,8,9,13,5,19,7,12,8,10,2,6,7,18,3,21,12,14,3,6,23,5,4,7,5,7}

2) А={14,11,7,8,6,15,5,12,7,17,8,11,2,6,9,12,3,21,12,14,3,8,23,3,4,8,3,7}

3) А={15,11,9,7,9,11,5,12,9,14,8,10,2,4,7,14,3,20,11,16,3,6,22,3,5,8,4,9}

4) А={10,11,9,8,9,15,5,12,7,14,8,10,2,6,7,18,3,21,12,14,3,6,23,3,4,8,6,9}

5) А={10,12,4,9,9,12,6,12,7,14,8,10,2,6,7,18,3,21,12,14,3,6,23,3,4,8,3,8}

6) А={14,14,6,8,5,11,7,13,7,17,8,12,2,6,7,18,3,21,12,14,3,6,23,3,4,8,6,9}

7) А={10,11,9,8,9,15,5,12,7,14,8,10,3,6,5,17,2,20,12,16,3,7,24,4,6,8,7,4}

8) А={16,11,4,8,7,16,8,10,4,12,8,13,3,8,7,14,5,23,10,13,5,6,27,4,5,9,6,3}

9) А={11,15,9,8,5,15,3,11,7,16,5,10,6,8,7,17,3,25,10,13,3,4,21,3,6,7,6,9}

Эйлеровы и гамильтоновы графы

Эйлеровымпутем в графе называется путь, содержащий все ребра графа.
Эйлеровым циклом в графе называется цикл, содержащий все ребра графа.

Связный граф G называется эйлеровым (см. рис. 7), если существует замкнутая цепь, проходящая через каждое его ребро только один раз. Такая цепь называется эйлеровой цепью. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым (см. рис. 8). На рис.9 приведен пример не эйлерова графа.

Рис.7. Эйлеров граф Рис.8. Полуэйлеров граф Рис.9. Не эйлеров граф

Критерий эйлеровости графа

Связный неориентированный граф является эйлеровым тогда и только тогда, когда степени всех его вершин (валентность) – чётные числа.

Следовательно, замкнутую фигуру, в которой все вершины - четные, можно начертить одним росчерком без повторений, начиная обводить ее с любой точки.

Формула Эйлера: Для всякого плоского представления связного плоского графа без перегородок число вершин (V), число ребер (E) и число граней [2] с учетом бесконечной (R) связаны соотношением V – E + R = 2.

Связный орграф содержит эйлеров контур тогда и только тогда, когда для каждой вершины число входящих дуг равно числу выходящих.

Пример: эйлеровым графом может быть план выставки. Это позволяет так расставить указатели маршрута, чтобы посетитель смог пройти по каждому залу в точности по одному разу.

Гамильтоновой цепью называется простая цепь, содержащая все вершины графа. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа.

Теорема Дирака: если в простом графе с n ³ 3 вершинами степень каждой вершины не меньше n/2, то такой граф обязательно будет гамильтоновым
(см. рис. 10).

Граф, который содержит простую цепь, проходящую через каждую его вершину, называется полугамильтоновым (см. рис. 11). На рис.12 приведен пример не гамильтонова графа.

Критерий же существования гамильтонова цикла в произвольном графе еще не найден.

 

Рис.10. Гамильтонов Рис.11. Полугамильтонов Рис.12. Не гамильтонов граф граф граф

Рассмотрим несколько достаточных условий существования гамильтоновых циклов в графе.

1) всякий полный граф является гамильтоновым. Действительно, он содержит такой простой цикл, которому принадлежат все вершины данного графа.

2) если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие ребра, то он также является гамильтоновым.

Пример: если гамильтонов граф объединить с еще одной вершиной ребром так, что образуется висячая вершина, то такой граф гамильтоновым не является, поскольку не содержит простого цикла, проходящего через все вершины графа.

 

Не является гамильтоновым и граф, представляющий собой простой цикл с "перекладиной", на которой расположены одна или несколько вершин

Примеры выполнения заданий

7)

1. Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо "красный", либо "синий" граф не является плоским.

Решение:

Пусть оба эти графа - плоские. Тогда у них вместе не более, чем
(3 · 11 - 6) + (3 · 11 - 6) = 54 ребра. Однако в полном графе с 11 вершинами 55 ребер. Противоречие.

Докажите, что граф, имеющий 10 вершин, степень каждой из которых равна 5, - не плоский.

Решение:

Не выполняется неравенство 3 V - 6 ≥ E.

Семиугольник разбит на выпуклые пяти- и шестиугольники, причем так, что каждая его вершина является вершиной по крайней мере двух многоугольников разбиения. Докажите, что число пятиугольников разбиения не меньше 13.

Решение:

Докажите сначала неравенство E £ 3V - 6, используя то, что из каждой вершины выходит по крайней мере 3 ребра. Обозначим количество пятиугольников через a, количество шестиугольников через b.

Заметим, что 5a + 6b + 7 = 2E £ 6F – 12 = 6(a + b + 1) – 12. Отсюда a ³ 13.

4. Граф задан геометрически. А) Определите, содержит ли данный граф гамильтонов цикл? Б) Выпишите гамильтонов цикл у данного графа, если он есть:

Решение:

А) да, содержит, т.к. граф – полный и не содержит перекладин и висячих вершин.

Б) гамильтонов цикл выделен сплошной линией: (1,2), (2,3), (3,4), (4,5), (5,1).

Задания для самостоятельного выполнения