Шесть функций сложного процента

 

Основой финансовой математики являются следующие шесть функций

сложного процента (или шесть функций денег):

1. Будущая стоимость единицы (накопленная сумма единицы) – FV (Future value).

2. Будущая стоимость аннуитета (накопление единицы за период) – FVA (Future value of an annuity).

3. Фактор фонда возмещения (периодический взнос в фонд накопления) – SFF (Sinking fund factor).

4. Текущая стоимость единицы (дисконтирование, реверсия ) – PV (Present value).

5. Текущая стоимость аннуитета – PVA (Present value of annuity).

6. Взнос на амортизацию единицы – IAO (Installment of amortize one).

Эти функции используются в различных финансовых расчетах. Рассмотрим каждую из этих функций с точки зрения ее математической формулировки и сферы применения.

 

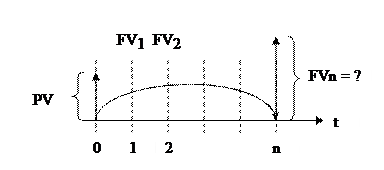
Функции наращения

Будущая стоимость денежной единицы (накопленная сумма единицы)

Данная функция позволяет определить будущую стоимость инвестированной денежной единицы, исходя из предполагаемых: ставки дохода (r), срока накопления (n) и периодичности (частоты) начисления процента (m):

FV = PV * (1+ r)n = PV * FМ1(r, n),

где FV – будущая стоимость денег;

PV – текущая стоимость денег;

r – ставка дохода;

n – число периодов накопления.

FМ1(r, n) = (1+ r)n – мультиплицирующий множитель, значения которого рассчитаны для разных значений (r) и (n) и представлены в соответствующих финансовых таблицах. Иногда его обозначают как FVIF (от англ. Future Value Interest Factor – процентный множитель будущей стоимости).

Экономический смысл множителя FМ1(r, n) состоит в том, что он показывает, чему будет равна одна денежная единица через (n) периодов при заданной процентной ставке (r). Справедливость формулы очевидна (рисунок 6.7).

Если на депозит положена сумма PV, то через один период начисления эта сумма станет равна:

FV1= PV + PV * r = PV * (1 + r),

через два периода она станет равна:

FV2= FV1+ FV1* r = FV1* (1+ r) = PV (1 + r)2,

и так далее через n периодов она станет равна:

FVn= FVn−1 + FVn−1* r = FVn−1* (1+ r) = PV (1 + r)n.

Рисунок 6.7 – Будущая стоимость денежной единицы

 

Пример. $1000 вложено в банк под 10 % годовых. Какая сумма накопится на счете через 5 лет? 10% переводим в относительные единицы, для этого делим их на 100% и получаем 10% / 100% =0,1.

FV5= 1000 (1+ 0,1)5= 1610,5.

Правило 72-х. Иногда при расчетах приходится сталкиваться с задачей определения количества периодов начисления, по истечении которых первоначально депонированная сумма увеличивается вдвое. Очень просто решить эту задачу позволяет известное «Правило 72-х», согласно которому – количество периодов, необходимое для удвоения первоначальной суммы вычисляется по формуле:

n = 72 / r.

 

Данное правило позволяет получить точные результаты при значениях r: 3% < r < 18%. Срабатывает правило и в обратном порядке для определения ставки дохода, при которой депонированная сумма удвоится.

Например, при ставке 6% годовых сумма удвоится за 72 / 6 = 12 лет.

Более частое, чем один раз в год, начисление процентов. Приведенные выше расчеты основывались на том предположении, что начисление процентов происходит один раз в год. Однако аккумулирование может происходить не только раз в год, но и чаще, например раз в квартал, раз в месяц и т. д. В этом случае необходимо ставку процента разделить на частоту накопления в течение года (m), а число лет накопления (n) умножить на частоту накопления в течение года (m). Формула расчета будет выглядеть следующим образом:

 

FV = PV (1 + r/m)n*m,

 

где m – частота начисления процентов в год;

n – число лет, в течение которых происходит накопление.

Чем чаще начисляются проценты, тем больше накопленная сумма. Приведенное преобразование справедливо в отношении всех шести функций.

 

6.2.1.2. Будущая стоимость аннуитета (накопление единицы за период)

Данная функция показывает, какой будет стоимость серии равных

платежей величиной (А) по истечении установленного срока их наращения (n) (рисунок 6.8).

Рисунок 6.8 – Будущая стоимость аннуитета постнумерандо

 

Из рисунка 6.8 видно, что будущая стоимость исходного денежного потока (аннуитета) постнумерандо (FVАpst) может быть оценена как сумма наращенных поступлений.

Очевидно, что будущая стоимость последнего платежа совпадает с величиной самого платежа, т.к. отсутствует период наращения:

FV0= А.

Будущая стоимость предпоследнего платежа будет наращена за один период и составит:

FV1= А·(1+r).

Аналогично наращиваются все платежи. Будущая стоимость первого платежа будет наращена за (n-1) периодов и составит:

FVn-1= А·(1+r) n-1.

Их общую сумму можно выразить как:

FVАpst = А·(1+r)n-1+ А·(1+r)n-2+...+ А·(1+r) + А

 

Вынесем (А) за знак скобки и обозначим (1+r) через (q). Получим выражение:

FVА = А·(qn-1+ qn-2+...+ q + 1).

 

Теперь отчетливо видно, что многочлен, содержащийся в скобках, называемый мультиплицирующий множитель и обозначаемый (FМ3(r, n)), представляет собой сумму членов геометрической прогрессии (S), но записанной в обратном порядке:

S = 1 + q + q2… + qn-2+ qn-1

 

Умножим обе части этого уравнения на (q) и получим:

 

S·q = q + q2… + qn-1+ qn

 

Вычтя из полученного уравнения предыдущее, получим:

 

S·q – S = qn–1.

Отсюда

S = (qn– 1) / (q – 1)

 

Теперь, подставив вместо (q) его значение (1+r), получаем формулу расчета мультиплицирующего множителя:

 

FМ3(r, n) = S = ((1+r)n– 1)/r

 

Следовательно, выражение для будущей стоимости обычного аннуитета величиной (А) за (n)периодов будет иметь вид:

 

FVАpst = А·FМ3(r, n) = А·((1+r)n– 1)/r).

 

Данный мультипликатор еще называют - процентный множитель будущей стоимости аннуитета FVIFA( r, n) – Future Value Interest Factor of Annuity. Экономический смысл мультиплицирующего множителя заключается в том, что он показывает, чему будет равна суммарная величина срочного (на определенный срок) накопленного аннуитета величиной в одну денежную единицу к концу срока его действия.

Поскольку значения множителя (FМ3(r, n)) зависит лишь от (r) и (n), то они рассчитаны для разных значений (r) и (n) и представлены в соответствующих финансовых таблицах.

Пример. Если вкладывать ежегодно $900 на счет в банке под 10% годовых, сколько накопится на нем через 5 лет?

 

FVА5= 900·((1+0,1)5− 1) / 0,1) = 5494,59

 

Теперь рассмотрим случая авансового аннуитета (рисунок 6.9).

Как и в случае обычного, рассмотрим накопленные суммы в конце первого, второго... n -го периода:

FV1= А·(1+r),

FV2= А·(1+r)2,

…………………………………………….……….

FVn= А· (1+r)n

FVАpre = А·(1+r)n+А·(1+ r)n −1+...+ А·(1+r)2+ А·(1+r).

Рисунок 6.9 – Будущая стоимость авансового аннуитета (пренумерандо)

 

Сравнив формулы расчета FVАpst и FVАpre, легко убедиться, что

 

FVАpre = FVАpst (1+ r).

 

Произведя соответствующее умножение, получим:

 

FVАpre = FVАpst·(1+ r) = А· ((1+r)n– 1)/r) (1+ r) =

= А· ((1+r)n+1– 1 – r)/r) = А· ((1+r)n+1– 1)/r) – 1).

 

Периодические депозиты могут вноситься чаще, чем один раз в год, соответственно чаще накапливается процент. При этом количество начислений увеличится в m раз и составит (n·m), а ставка уменьшится в m раз и составит (n/m). Тогда ранее полученная формула примет вид:

 

FVАn= А·(((1+r/m)(n+1)m– 1)/r/m) – 1).

 

Чем чаще делаются взносы, тем больше накопленная сумма.

Пример. Если вкладывать ежемесячно $75 на счет в банке под 10 % годовых, сколько накопится на нем через 5 лет?

FVА5= 75 (((1+0,1/12) 5·12– 1) / 0,1/12 = 5807,78.

 

Фактор фонда возмещения

Данная функция позволяет рассчитать величину периодического платежа (А или SFF, как его в таком случае называют), необходимого для накопления нужной суммы (FVА) по истечении (n)платежных периодов при заданной ставке процента (r) (рисунок 6.10).

Рисунок 6.10 – Периодический взнос в фонд накопления

 

Из формулы будущей стоимости аннуитета (FVА = А·FМ3(r, n)) следует, что величина каждого платежа (SFF или А) в случае обычного аннуитета вычисляется следующим образом:

 

SFFpst = Аpst = FVА / FМ3(r, n) = FVА·r/((1 + r)n− 1) = FVА·FМ5(r, n).

 

где FМ5(r, n) = r/((1 + r)n− 1) – мультиплицирующий множитель, значения которого рассчитаны для разных значений (r) и (n) и представлены в соответствующих финансовых таблицах.

Экономический смысл множителя FМ5(r, n) состоит в том, что он показывает величину периодических платежей необходимых для накопления одной денежной единицы через (n) периодов.

Пример. Необходимо за 4 года скопить $1000 при ставке банка 10%. Сколько придется вкладывать каждый год?

SFF = 1000 (0,1 / ((1 + 0,1)4− 1) = 215,47.

 

В случае авансового фонда возмещения (соответствующего авансовому аннуитету) формула единичного платежа (SFFpre) имеет вид:

 

SFFpre = FVА·r/((1 + r)(n+1)− 1− r).

Функции дисконтирования