Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квартили, перцентили, децили распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
С целью более подробного изучения структуры вариационного ряда рассчитывают квартили, децили, перцентили, расчет которых подобен расчету медианы. Квартили Q – структурные характеристики, делящие ранжированный ряд на 4 части, равные по числу единиц:
Задача №5 На основании данных интервального ряда распределения фирм по среднесписочной численности работников рассчитать квартили и сделать выводы. Решение: На базе таблицы 2 составим вспомогательную таблицу: Таблица 6 – Вспомогательная таблица для расчета квартилей
Определяем Q1 Таким образом, первая четверть фирм исследуемого ряда распределения имеет среднесписочную численность работников менее 29 человек, другие три четверти – более 29 человек.
Таким образом, первые три четверти фирм исследуемого ряда имеют среднесписочную численность работников менее 38 человек, оставшаяся часть более 38 человек. Децили – значения признаков, которые делят ранжированный ряд на десять равных частей. Перцентили – значения признаков, которые делят ранжированный ряд на сто равных частей. Графическое определение моды и медианы Приближенное модальное значение можно определить и графически – по гистограмме. Для этого нужно взять столбец, имеющий наибольшую высоту, и из его левого угла провести отрезок в верхний угол последующего столбца, а из правого угла – в верхний правый угол предыдущего. Абсцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности. Медиану можно графически определить по полигону. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с полигоном. Абсцисса точки пересечения и является медианой. Задача №6 На основании данных интервального ряда распределения фирм по среднесписочной численности работников определить моду и медиану графическим способом.
Решение:
Применение моды и медианы Медиана характеризует деление совокупности на две половины. Медиана находит применение, когда средняя является дробным числом, не имеет реального смысла, например, число человек (3,5 человека, проживающего в одной квартире). Мода применяются в экономике при исследовании производительности труда, норм выработки, позволяет выявить наиболее распространенный размер или уровень изучаемого явления. Изучение моды и медианы экономических явлений помогает выявлению неиспользованных резервов производства. 6 Задачи для самостоятельного решения Задача №8 Имеются данные о месячном заработке отдельных рабочих в бригаде, состоящей из 14 человек: 90, 94, 94, 102, 102, 102, 102, 102, 110, 110, 110, 116, 116, 120 руб. Представьте эти данные в виде ряда распределения. По какому признаку будет построен этот ряд? Решение: Данный ряд распределения будет построен по вариационному признаку Таблица 7 – Ряд распределения
Задача №9 Определить по решению задачи №8 моду и медиану. Решение: Модой будет являться заработок в 102 руб., т.к. он имеет наибольшую частоту. Определим порядковый номер медианы: медиана будет равна 7,5, т.е. медиана расположена между значениями 7 и 8 Задача №10 Вычислить моду и медиану для следующего вариационного ряда: Таблица 8 – Вариационный ряд
Решение: Используя формулы моды и медианы, подставляя значения, находим:
Мода и медиана оказались в одном интервале, но их значения не одинаковы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 727; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.92.173 (0.01 с.) |



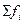
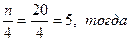

 по решению задачи №3 Определяем Q3
по решению задачи №3 Определяем Q3 



 , т.к. число 102 приходятся на середину ранжированной совокупности.
, т.к. число 102 приходятся на середину ранжированной совокупности.