
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие понятия о структурных среднихСодержание книги
Поиск на нашем сайте
В некоторых случаях возникает необходимость дать такую характеристику типичных размеров варьирующего (изменяющегося) признака, которая является одним из конкретных чисел, имеющихся в вариационном ряду. Например, при установлении размера одежды или обуви, имеющего наибольший покупательский спрос, исчисленная средняя арифметическая не дает конкретного размера, в результате вычислений можно получить средний размер одежды или обуви, который не соответствует существующим размерам, например, 49,4, т.к. в действительности имеются размеры 48 и 50. Поэтому в статистической практике применяются еще и такой вид средних величин, как структурные средние – мода и медиана. Структурные характеристики – это особый вид средних величин, которые применяются для изучения внутреннего строения ряда распределения, а также оценки средней величины, если по статистическим данным ее нельзя рассчитать. Мода – значение признака, которое имеет наибольшую частоту в статистическом ряду распределения (Мо). Мода широко применяется при изучении покупательского спроса, регистрации цен. Мода определяется по следующей формуле:
где Мо – мода, х0 – нижняя граница модального интервала,
Задача №1 На основании следующих данных построить ряд распределения: 35, 26, 20, 34, 30, 33, 28, 35, 42, 27, 36, 22, 25, 35, 32, 50, 31, 33, 41, 41. Данные отражают информацию о численности человек на предприятиях отрасли. Решение: Ряд распределения строится по вариационному признаку, т.к. численность – количественный признак, дискретный ряд распределения, т.к. построен по целым числам. По формуле Стерджесса рассчитаем количество интервалов: к=1+3,32lgn, где n – совокупность (20 фирм) к=1+3,325lg20=1+33,2×1,301=5,32. У нас есть выбор: мы можем взять 5 или 6 интервалов, т.к. лучше, чтобы было больше интервалов, а длина интервала была меньше возьмем 6 интервалов, Длину интервала определяем по формуле:
Группы интервалов: 20-25, 25-30, 30-35, 35-40, 40-45, 45-50 (так длина интервала – 5) Таблица 1 – Ряд распределения по численности человек
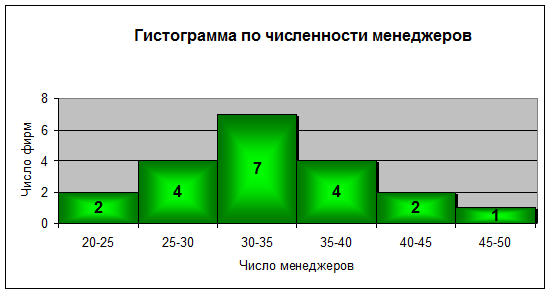
По данным таблицы построить гистограмму, отражающую численность менеджеров в фирмах:
Задача №2 На основании данных интервального ряда распределения фирм по среднесписочной численности человек рассчитать моду и сделать вывод. Таблица 2 – Ряд распределения по численности человек
Решение: Модальный интервал 30-35, т.к. его частота максимальна (7). Определим для модального интервала точное значение моды:
Ответ: таким образом, чаще всего встречаются фирмы с численностью 33 человека.
Медиана – это значение варьирующего признака, расположенное в середине упорядоченного вариационного ряда, делящей его на две равные части таким образом, что половина единиц совокупности имеет значение признака меньше, чем медиана, а вторая – больше, чем медиана. Медиана определяется по следующей формуле: где Ме – медиана, х0 – нижняя граница медианного интервала,
Пример: Представлен ряд распределения по сумме заработной платы рабочих:
В этом ряду среднее место по размеру заработной платы занимает рабочий с номером 4, получивший 1600 руб. Эта величина и есть медиана. Меньше и больше медианы одинаковое число вариантов. При определении порядкового номера медианы используется следующая формула: Задача №3 На основании данных вариационного ряда распределения фирм по среднесписочной численности менеджеров рассчитать моду и сделать вывод. Таблица 3 – Вспомогательная таблица для расчета медианы
Решение:
Определяем медианный интервал. Медианный интервал 30-35, т.к. накопленная частота именно в этом интервале превысила величину, равную половине объема распределения:
Таким образом, одна половина фирм имеет численность менеджеров меньше 33 человек, вторая больше. Свойство медианы У медианы есть отличительное свойство: Проиллюстрируем это свойство. Задача №4 Определить медиану и сумму абсолютных отклонений на основе следующей таблицы:
Таблица 4 – Исходные данные
Решение: Медианой для данной таблицы будет является длина, равная 6 см, А=3 см. если наибольшее значение признака равно 3, то абсолютная сумма отклонений равна 29, и эта сумма больше, чем сумма отклонений от медианы. Таблица 5 – Решение задачи
Это свойство имеет важное значение для решения практических задач, например, расчета самого короткого пути из всех возможных для транспорта и т.п.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.152 (0.011 с.) |

 ,
, – верхняя граница модального интервала,
– верхняя граница модального интервала, – частота модального интервала,
– частота модального интервала, – частота интервала, предшествующего модальному,
– частота интервала, предшествующего модальному, – частота интервала, следующего за модальным
– частота интервала, следующего за модальным


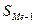 – накопленная частота интервала, предшествующего медианному,
– накопленная частота интервала, предшествующего медианному,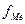 – частота медианного интервала
– частота медианного интервала .
.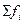
 , объем ряда распределения – 20 фирм. Определяем для медианного интервала ряда распределения точное значение моды:
, объем ряда распределения – 20 фирм. Определяем для медианного интервала ряда распределения точное значение моды:
 , т.е. сумма абсолютных отклонений значений признака у всех единиц ряда распределения от медианы меньше, чем сумма отклонений от любого значения признака у единицы в данном ряду распределения.
, т.е. сумма абсолютных отклонений значений признака у всех единиц ряда распределения от медианы меньше, чем сумма отклонений от любого значения признака у единицы в данном ряду распределения.




