Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Середня хронологічна. Приклад.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Середня хронологічна використовується для осереднення моментних показників. Якщо є два моментних показника (на початок і на кінець періоду), то середня розраховується як півсума значень за формулою:
Наприклад: Капітал банку на початок І кварталу 50 млн.у.г.о., а на кінець – 60 млн.у.г.о. Обчислимо середній розмір капіталу банку за І квартал.
Якщо моментів більше ніж два, а інтервали часу між ними рівні, то у чисельнику до півсуми крайніх значень додають усі проміжні, а знаменником є число, яке на одиницю менше від числа значень ознаки.
Така формула називається середньою хронологічною. Наприклад: Залишки коштів на рахунку клієнта у банку на початок кожного місяця становили, тис.грн.: липень - 50, серпень - 60, вересень - 62, жовтень - 80. Обчислимо середньомісячний залишок коштів за ІІ квартал.
Середня гармонічна. Приклад. Для осереднення обернених показників використовується середня гармонічна. Якщо дані не згруповані, то використовується середня гармонічна проста:
Для згрупованих даних використовують середню гармонічну зважену:
Середня гармонічна зважена використовується тоді, коли в логічній формулі середньої за умовами задачі відомий чисельник, крім значень ознаки, а знаменник невідомий. Приклад: Маємо дані про показники заробітної плати в комерційному банку
Визначити середню заробітну плату за місяць одного працівника по двох відділах у цілому. Розв¢язування: Побудуємо логічну формулу:
Фонд з/п Кількість працівників (f) невідома, її можна знайти, якщо W/X = 4200/600 і 3500/700. Підставимо дані у формулу:
Таким чином, середня гармонічна зважена використовується тоді коли в логічній формулі середньої за умовами задачі відомий чисельник, а знаменник – ні. Середня геометрична. Приклад. Середня геометрична використовується для осереднення ланцюгових відносних величин динаміки і розраховується за формулою:
де П - символ добутку; х - ланцюгові відносні величини динаміки. Приклад: Показники діяльності банківської системи України (Бюлетень НБУ № 1, 2005 р.).
Визначте середньорічне зростання емісії готівки і грошової маси Розв‘язування: Обчислимо: 1) зростання емісії готівки у середньому за рік
2) зростання грошової маси
Щороку емісія готівки у середньому зростала в 1,318 раза або на 31,8 % (131,8 -100), а грошова маса Середня квадратична. Середня квадратична використовується в статистиці при розрахунках показників варіації, а формула її буде такою:
Частотні характеристики рядів розподілу. Характерні риси та особливості структури статистичної сукупності відображаються в рядах розподілу (атрибутивних та варіаційних). Частотними характеристиками будь-якого ряду є: - частота (f) - частка (d).
Якщо інтервали варіаційного ряду нерівні, то використовують щільність частоти (частки) на одиницю інтервалу, яка розраховується за формулами: q = f: h, де h - ширина інтервалу, або q = d: h Приклад: Розподіл клієнтів банку за розмірами вкладів:
Згідно зі значеннями кумулятивних часток у більшості клієнтів (50,6%) розмір вкладу не перевищує 5 тис. грн. Щільність розподілу зі зростанням ширини інтервалу зменшується. Найбільшу щільність розподілу має перша група клієнтів з розміром вкладу 1 –2 тис. грн.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.192 (0.011 с.) |

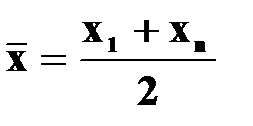 ,
,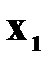 - значення показника на початок періоду;
- значення показника на початок періоду;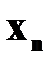 - значення показника на кінець періоду.
- значення показника на кінець періоду.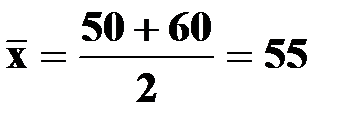 млн.у.г.о.
млн.у.г.о.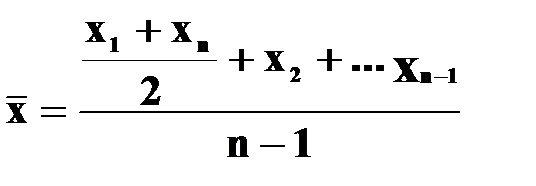
 тис. грн.
тис. грн.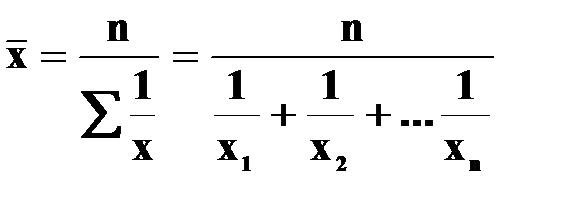
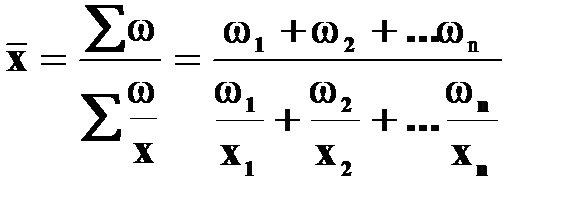 , де
, де 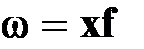 - обсяг значень ознаки
- обсяг значень ознаки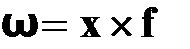
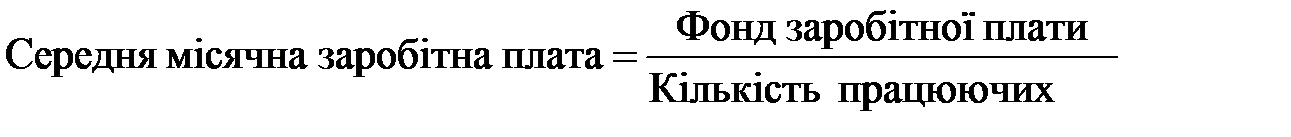
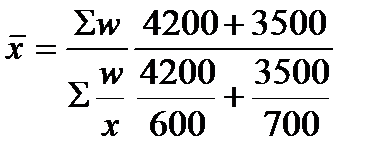 =
= 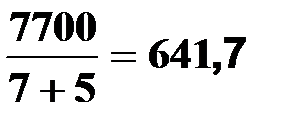 грн.
грн.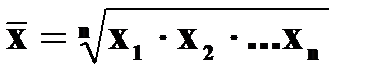 =
= 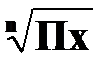 ,
,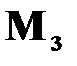 )
)
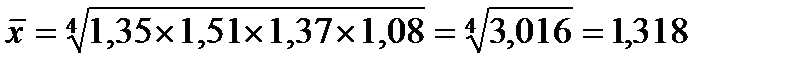 або 131.8%
або 131.8% у середньому за рік
у середньому за рік
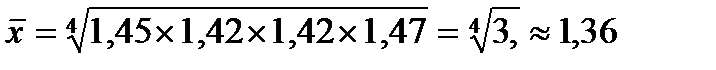 …
…