
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистична перевірка гіпотез.Содержание книги Поиск на нашем сайте
Дані вибіркових спостережень часто становлять основу для прийняття одного з кількох альтернативних рішень (продукція може бути бракованою або якісною, точність обробки виробу в межах норми або нижча від норми і т. д.). Із загальнометодологічного погляду тут йдеться про висунення деякої гіпотези, яку відхиляють або приймають після проведення деякого експерименту. Якщо цей експеримент має статистичний (стохастичний) характер, кажуть, що гіпотеза є статистичною. Означення. Статистичною називають гіпотезу про властивості генеральної сукупності, що перевіряється на основі вибірки. Статистичними гіпотезами можуть бути, наприклад, такі твердження: розподіл імовірностей випадкової величини є нормальний; розподіл імовірностей випадкової величини є пуассонівський; у нормальному розподілі випадкової величини параметри У математичній статистиці виділяють два основні типи статистичних гіпотез: · гіпотези про закон розподілу ймовірностей випадкової величини (ознаки генеральної сукупності); · гіпотези про значення параметрів розподілу випадкової величини (ознаки генеральної сукупності). Статистичні гіпотези першого типу називають непараметричними, а другого типу – параметричними. Означення. Основною (нульовою) називають висунуту гіпотезу і позначають Альтернативною (конкуруючою) називають гіпотезу, яка повністю або частково логічно заперечує нульову гіпотезу, і позначають Наприклад, математичне сподівання нормально розподіленої випадкової величини Задача про статистичну перевірку статистичних гіпотез фомулюється так. Розглядають деяку гіпотезу про те, що розподіл імовірностей деякої випадкової величини має той чи інший вигляд, або параметри розподілу мають ті чи інші значення. Задача полягає у тому, щоб на основі вивчення статистичних даних (вібірки) підтвердити справедливість висунутої гіпотези чи спростувати її. При цьому вказується також імовірність того, що прийняте рішення є правильним або помилковим. Проблема зменшення ймовірності того, що прийняте рішення є помилковим, є також однією із задач математичної статистики.
У результаті статистичної перевірки гіпотези може бути прийняте одне з двох правильних рішень: 1) гіпотеза приймається і вона істинна; 2) гіпотеза відхиляється і вона неістинна. Поряд із тим у результаті статистичної перевірки статистичної гіпотези можуть бути допущені помилки (прийняті неправильні рішення) двох типів: 1) гіпотеза відхиляється, але вона істинна (помилка першого роду); 2) гіпотеза приймається, але вона неістинна (помилка другого роду). Виявляється, що помилка першого роду має вагоміші наслідки, ніж помилка другого роду. Щоб застрахувати себе від помилки першого роду або принаймні звести до мінімуму ризик її допущення, вводиться спеціальне число Означення. Імовірність допущення помилки першого роду називають рівнем значущості і позначають через Число
58.Аналіз таблиць взаємної спряженості. Міжгрупова дисперсія обчислюється за формулою: Відношення міжгрупової дисперсії до загальної є мірою щільності зв’язку в моделі аналітичного групування і називається кореляційним відношенням
Кореляційне відношення коливається від 0 до 1, а якщо подається у процентах, то від 0до 100% і показує, скільки процентів варіації результативної ознаки пов’язано з варіацією факторної ознаки. Чим більше Однак, навіть щільний зв’язок може виникнути випадково, тому слід перевірити його істотність, тобто довести не випадковість зв’язку. Перевірка істотності зв’язку – це порівняння фактичного значення
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.107.50 (0.009 с.) |

 і
і  у показниковому розподілі випадкової величини параметр
у показниковому розподілі випадкової величини параметр  випадкові величини Х і Y незалежні і т. п.
випадкові величини Х і Y незалежні і т. п.

 основна гіпотеза; математичне сподівання нормально розподіленої випадкової величини
основна гіпотеза; математичне сподівання нормально розподіленої випадкової величини  альтернативна гіпотеза. Записують це так:
альтернативна гіпотеза. Записують це так: 
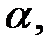 яке виражає ймовірність відхилення правильної гіпотези.
яке виражає ймовірність відхилення правильної гіпотези.
 задають наперед і найчастіше його вибирають рівним 0,1; 0,05; 0,01. Якщо
задають наперед і найчастіше його вибирають рівним 0,1; 0,05; 0,01. Якщо  то це означає, що ймовірність допустити помилку першого роду є мала, а саме – ми ризикуємо її допустити у 5-ти випадках зі 100.
то це означає, що ймовірність допустити помилку першого роду є мала, а саме – ми ризикуємо її допустити у 5-ти випадках зі 100.
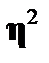 наближається до одиниці, тим щільніший зв’язок. За відсутності зв’язку
наближається до одиниці, тим щільніший зв’язок. За відсутності зв’язку  для певного рівня істотності d та кількості ступенів свободи
для певного рівня істотності d та кількості ступенів свободи 
 , m – кількість груп; n – обсяг сукупності. Якщо фактичне значення
, m – кількість груп; n – обсяг сукупності. Якщо фактичне значення 


