
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5: показатели вариации признака в совокупности (2 ч)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 1: 2. По данным обследования получено следующее распределение студентов-заочников по возрасту на факультете:
Рассчитайте: 1) средний возраст студента-заочника на факультете; 2) показатели вариации. Сформулируйте выводы. Решение: 1) средний возраст студента-заочника определим по формуле средней арифметической взвешенной, так как отдельные значения исследуемой совокупности встречаются не один, а много, причем неодинаковое число раз, т.е. представляют собой ряд распределения.
2) показатели вариации: Построим вспомогательную таблицу:
Размах вариации
Среднее линейное отклонение.
Дисперсия и среднее квадратическое отклонение.
Коэффициент вариации.
Так как, коэффициент вариации …… 33%, то совокупность можно считать ………………... Задача 2: По данным выборочного обследования зарплаты работников бюджетной сферы получены следующие показатели:
Определите: 1) среднюю зарплату работников по двум отраслям; 2) дисперсии зарплаты: а) среднюю из внутригрупповых дисперсий (отраслевых) б) межгрупповую (межотраслевую) в) общую 3) коэффициент детерминации и эмпирическое корреляционное отношение; 4) сделайте выводы. Решение: 1. Средняя заработная плата работников по двум отраслям равна
2. а) Средняя из групповых дисперсий равна
б) Межгрупповая дисперсия равна
в) Применяя правила сложения дисперсий, получим общую дисперсию:
3. а) Коэффициент детерминации равен
Он показывает, что оплата труда на …..% зависит от отраслевой принадлежности работников и на ……% - от внутриотраслевых причин. б) Эмпирическое корреляционное отношение составляет
, что свидетельствует о существенном влиянии на дифференциацию заработной платы отраслевых особенностей. Задача 3: Имеются данные о чистой прибыли банков двух районов:
Рассчитайте дисперсии чистой прибыли: внутригрупповые (по каждому району), среднюю из внутригрупповых, межгрупповую и общую. Решение. Средняя внутригрупповая дисперсия свидетельствует о случайной вариации, которая может возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от признака-фактора, положенного в основу группировки. Данная дисперсия рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным группам, затем рассчитывается средняя внутригрупповая дисперсия. Внутригрупповые дисперсии определим по формуле:
Средняя из внутригрупповых дисперсий равна
Межгрупповая дисперсия (дисперсия групповых средних) характеризует систематическую вариацию, т.е. различия в величине исследуемого признака, возникающие под влиянием признака-фактора, который положен в основу группировки. Межгрупповая дисперсия определяется по формуле:
Общая дисперсия (по правилу сложения дисперсий) равна
ТЕМА 6: МЕТОДЫ АНАЛИЗА ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ (3 ч). Задача 1. По ниже приведенным данным, характеризующим динамику производства валового выпуска продукции предприятия по месяцам, требуется: 1) осуществить сглаживание ряда, применяя трехмесячную скользящую среднюю; 2) проанализируйте полученный ряд динамики, используя следующие показатели: - цепные и базисные: абсолютные приросты, темпы роста, темпы прироста, - абсолютное значение одного процента прироста; - среднегодовые: абсолютный прирост, темп роста, темп прироста. Сделайте выводы.
Решение: 1) осуществим сглаживание ряда, применяя трехмесячную скользящую среднюю за январь-март:
за февраль-апрель:
Результаты расчета трёхлетней скользящей средней представлены в таблице:
В результате обработки ряда динамики методом скользящей средней проявилась тенденция к росту производства валового выпуска продукции предприятия. Недостатком способа сглаживания рядов динамики является то, что полученные средние не дают теоретических рядов, в основе которых лежала бы математически выраженная закономерность. 2) проанализируем полученный ряд динамики, используя следующие показатели:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.217.176 (0.011 с.) |



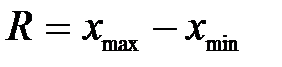 = лет
= лет =
= =
= =
=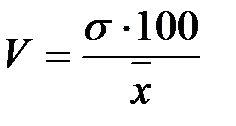 = %
= %






 =(63+93+102)/3 = 168/3 = 56 млн. руб.
=(63+93+102)/3 = 168/3 = 56 млн. руб.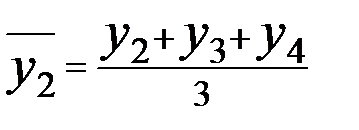 = (93+102+117)/3 = 312/3 = 104 млн. руб.
= (93+102+117)/3 = 312/3 = 104 млн. руб.
 =(
=( )/ n
)/ n



