
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 9: выборочный метод. (2 ч)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 1: Производится выборочная 5% разработка данных об успеваемости студентов дневного отделения вуза одного из факультетов по результатам зимней сессии. Результаты следующие.
Принимая во внимание, что отбор был собственно случайным и бесповторным, определите с вероятностью 0,954 по факультету в целом: 1. пределы, в которых находится средний балл успеваемости в целом по факультету. 2. пределы, в которых находится доля студентов сдавших экзамены на «хорошо» и «отлично». Решение: 1. Средняя успеваемость в генеральной совокупности (для факультета в целом) находится в доверительном интервале или в следующих пределах.
Где
Где t- это коэффициент доверия, который определяется по таблице интегральных функций Лапласа (при р = 0,954; t = 2; при р = 0,997; t = 3)
С вероятностью 0,954 можно утверждать, что средний балл успеваемости в целом по факультету составляет……………….. 2. Доверительные интервалы или пределы, в которых находятся студенты, получившие на сессии хорошо и отлично, представляют собой:
Т.е., с вероятностью 0,954 можно гарантировать, что доля студентов сдавших экзамены на «хорошо» и «отлично» составляет в целом по факультету …… Задача 2: В области, состоящей из 20 районов, проводилось выборочное обследование урожайности зерновых на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16; 15,5; 15 и 14 ц/га. С вероятностью 0,954 найдите пределы урожайности во всей области. Решение. Рассчитаем общую среднюю:
Межгрупповая (межсерийная) дисперсия составит:
Определим предельную ошибку серийной бесповторной выборки (t=2, при p=0,954): D= t* Следовательно, урожайность в области с вероятностью 0,954 будет находиться в пределах:
Таким образом, средняя урожайность в районе находится в пределах от ….. Задача 3: Для определения среднего возраста женщин, вступающих в брак, в городе была произведена 5% типическая пропорциональная выборка. Результаты обследования представлены в следующей таблице.
С вероятностью 0,997 установите границы доли женщин, вступающих второй раз в брак в городе.
Решение: Доля женщин, вступающих во второй брак, будет находиться в пределах: ω- ∆≤ p ≤ ω+ ∆. Выборочную долю определим по формуле:
Выборочную дисперсию альтернативного признака определим по формуле:
Предельную ошибку определим по формуле:
С вероятностью 0,997 можно утверждать, что доли женщин, вступающих во второй брак, будет находиться в пределах:
Задача 4: В городе Н проживает 100 тыс.чел.. с помощью механической выборки определите долю населения со среднедушевыми денежными доходами до 5000 руб. в месяц. Какова должна быть численность выборки, чтобы с вероятностью 0,997 ошибка выборки не превышала 2%, если на основе предыдущих обследований известно, что дисперсия равна 0,24? Решение:
Определим необходимую численность выборки по формуле для бесповторного отбора:
=
Учебно-методическое и информационное обеспечение дисциплины (модуля) Основная литература 1. Общая теория статистики: Учебник / под ред. М.Г. Назарова - M.: Омега - Л, 2010.- 410с. 2. Статистика [Электронный ресурс]: учебник / под ред. Елисеевой И.И.– 4-е изд., пер. и доп. – М.: Издательство Юрайт, 2014 – 674 с. Режим доступа http://www.biblio-online.ru 3. Статистика [Электронный ресурс]: учебник / под ред. В.С. Мхитаряна – М.: Издательство Юрайт, 2015 – 590 с. Режим доступа http://www.biblio-online.ru 4. Статистика: Учебник / под ред. С.А. Орехова - M.: ЭКСМО, 2010.- 448с. 5. Теория статистики [Электронный ресурс]: учебное пособие / под ред. В.В. Ковалева – М.: Издательство Юрайт, 2015 – 454 с. Режим доступа http://www.biblio-online.ru
Дополнительная литература. 1. Булетова, Н.Е. Статистика. Часть 1. Теория статистики.: Учебно-методическое пособие / Н.Е. Булетова - Волгоград: Изд-во ВАГС, 2005.- 76с. 2. Годин, А.М. Статистика: Учебник / А.М. Годин - M.: Дашков и К, 2003.- 472с. 3. Ефимова, М.Р. Общая теория статистики: Учебник / М.Р. Ефимова, Е.В. Петрова, В.Н. Румянцев - M.: ИНФРА-М, 2009.- 416с. 4. Краснобокая, И.А. Статистика: лабораторный практикум: учеб.-метод. пособие / И.А. Краснобокая, А.В. Чернова. - Орел: Изд-во ОРАГС, 2004. - 108 с. 5. Лялин, В.С. Статистика: теория и практика в Excel [Электронный ресурс]: учебное пособие / В.С. Лялин, И.Г. Зверева, Н.Г. Никифорова – М.: Финансы и статистика, 2010 – 448 с. Режим доступа http://e.lanbook.com
6. Лясковская, О.В. Ряды динамики: методические указания по выполнению типового расчета по курсу «Статистика»: Методические рекомендации / О.В.Лясковская, Е.В.Чаева - Орел: Изд-во ОРАГС, 2009.- 29с 7. Морозова, А.В. Статистика: опорный конспект лекционного курса: Учебное пособие / Под ред. В.Г. Шуметова - Орел: Изд-во ОРАГС, 2006.- 124с. 8. Статистика: Учебник / Под ред. И.И. Елисеевой - M.: ТК Велби, 2006.- 448с. 9. Статистика: Электронный учебник: Учебник / Под ред. М.Г. Назарова - M.: КНОРУС, 2009. 10. Теория статистики: [Электронный ресурс]: учебник / Р.А. Шмойлова, В.Г. Минашкин, Н.А. Садовникова, Е.Б. Шувалова; под ред. Р.А. Шмойловой – 5-е изд. – М.: Финансы и статистика, 2014 – 656 с. Режим доступа http://e.lanbook.com 11. Тимофеева С.А. Статистика: учебник./ И.И.Сергеева, С.А.Тимофеева, Т.А. Чекулина – 2-е изд. испр. и доп. - М.: ИД «ФОРУМ»: ИНФРА-М, 2011. – 304с. 12. Теория статистики с элементами эконометрики. Практикум [Электронный ресурс]: учебное пособие / под ред. Ковалева В.В.– М.: Издательство Юрайт, 2015 – 386 с. Режим доступа http://www.biblio-online.ru
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.167.15 (0.006 с.) |

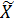 -
- 
 +
+  = t
= t 
 =
=  =
=
 = t
= t  =
= =
= *t
*t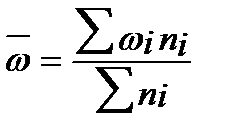 =
=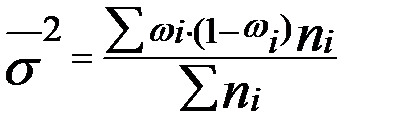 =
= =
=



