
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4: абсолютные, относительные и средние величины (2 Ч).Содержание книги
Поиск на нашем сайте
Задача 1: Среднегодовая численность населения области в 2015 г. была 3540,7 тыс. человек. Из них занято в экономике 1926,2 тыс. чел. (в 2014 г. было занято 1957,1 тыс. чел. при общей численности населения 3418,1 тыс. чел.), безработные составили 55,4 тыс. чел. Среди безработных лица с высшим образованием – 3 тыс. чел., молодежь в возрасте от 16 до 29 лет – 7,8 тыс. чел., женщины – 38,4 тыс. чел. Определите относительные величины динамики, структуры, координации и интенсивности. Сделайте выводы.
Решение: 1. ОПД = ОПД =
Т.о., за год численность населения……
2. ОПС =
ОПСвыс =
ОПСмол =
ОПСж =
Таким образом, …..
3. ОПК = часть 1/ часть 2
ОПК =
Т.е.,
4. ОПИ = Задача 2: По данным фирмы имеются следующие данные, в млн. руб.
Определите в целом по фирме: 1) размер планового задания по росту объёма реализованной продукции в отчётном году; 2) процент выполнения плана; 3) показатель динамики реализованной продукции. Решение: 1. ПЗ =.
ОППЗ =
ОППЗ =
2. ОПВП =
ОПВП =
3. ОПД =
Таким образом, фирма в целом……. Задача 3: Предприятием были выделены одинаковые денежные суммы на приобретение акций 2-х видов, при этом цена вида акций А - 1000 руб., а вида В - 1800 руб. Рассчитайте среднюю цену акции. Решение: Так как, в исходных данных совокупные показатели денежной суммы не известны, но сказано, что они одинаковы, а известны только индивидуальные значения признака, то для расчета воспользуемся средней гармонической простой:
Задача 4. Списочная численность работников фирмы в 2015 г. составила: на 1 января – 530 человек, на 1 марта – 570, на 1 июня – 520, на 1 сентября – 430, а на 1 января 2016 г. – 550 человек. Определите среднегодовую численность работников фирмы за 2015 г. Решение: Так как, в качестве исходных данных используются моментные показатели списочной численности работников фирмы за целый год по месяцам, то для расчета среднегодовой численности работников фирмы за 2015 год воспользуемся формулой средней хронологической простой:
Задача 5: Имеются следующие данные о коэффициентах роста среднедушевых доходов населения:
Определите средний коэффициент роста доходов населения. Решение: Так как, в исходных данных представлены относительные величины в виде перечня показателей, то воспользуемся формулой средней геометрической простой:
Задача 6. Имеются данные о финансовых показателях фирм за два периода:
Определите среднюю прибыль на одну акцию по двум фирмам в каждом периоде. Решение:
Задача 7: Ниже приведены следующие данные о распределении безработных мужчин и женщин, имеющих опыт работы, по продолжительности поиска работы в 2015 г.:
Определите: 1) численность безработных мужчин и женщин в тыс.чел. 2) среднюю продолжительность поиска работы: а) для женщин; б) для мужчин; в) для всех безработных в целом; 3) моду и медиану в каждой группе. Решение: Построим вспомогательную таблицу:
Определим: 1) среднюю продолжительность поиска работы по формуле средней арифметической взвешенной по удельным весам:
а) для женщин
б) для мужчин
в) для всех безработных в целом
2) моду и медиану в каждой группе Мода (Мо) – это наиболее часто встречающаяся в ряду варианта. В интервальном вариационном ряду определяется модальный интервал. Конкретное значение моды для интервального ряда определяется формулой:
где
Медиана (Ме) – это срединное значение варьирующего признака в упорядоченном (ранжированном) ряду. Применяется в случаях, когда совокупность статистических данных неоднородна (асимметрична), поскольку Ме менее чувствительна к средним значениям ряда, чем средняя арифметическая. Формула медианы в интервальном ряду распределения будет иметь следующий вид:
где
Модальный интервал равен более 12 месяцев, так как частота его максимальная как для мужчин (37%), так и для женщин (41,1%). Медианный интервал равен 6-9 месяцев, так как находится в середине совокупности или интервального ряда распределения, в котором содержится нечетное количество групп.
Для женщин
Мо =
Ме =
Для мужчин Мо =
Ме =
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.107 (0.011 с.) |

 =
= %
%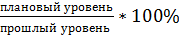

 .гарм. =
.гарм. =  =
= = человек
= человек =
= =
=

 =
= =
= =
=
 - нижняя граница модального интервала;
- нижняя граница модального интервала; - величина модального интервала;
- величина модального интервала; - частота, соответствующая модальному интервалу;
- частота, соответствующая модальному интервалу; - частота, предшествующая модальному интервалу;
- частота, предшествующая модальному интервалу; - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
 - нижняя граница медианного интервала;
- нижняя граница медианного интервала; - величина медианного интервала;
- величина медианного интервала; - полусумма частот ряда;
- полусумма частот ряда; - сумма накопленных частот, предшествующих медианному интервалу;
- сумма накопленных частот, предшествующих медианному интервалу; - частота медианного интервала.
- частота медианного интервала.


