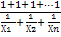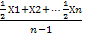Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значение стоимостных показателей в оценке результатов экономической деятельности.Содержание книги
Поиск на нашем сайте
СТОИМОСТНЫЕ ПОКАЗАТЕЛИ — показатели, характеризующие экономические явления в стоимостном (денежном) выражении и определяемые с помощью цен. Средние величины. Средней величиной в статистике называется обобщающий показатель, котором характеризует типичный уровень варьирующегося признака в расчете на единицу совокупности в конкретных условиях места и времени. В статистике применяются различные виды средних величин: средняя арифметическая простая и взвешенная; средняя гармоническая, средняя хронологическая, средняя геометрическая и др. Однако, средние величины не всегда дают исчерпывающую характеристику статистической совокупности. Средняя не позволяет объективно оценить явления вследствие сильного влияния аномальных максимальных или минимальных значений. Виды средних величин: 1. Средняя арифметическая простая, она равна частному от деления суммы индивидуальных значений признака на их количество: х – значение признака; х – среднее значение n – количество признаков.
х =
2. Средняя арифметическая взвешенная равна сумме произведений признака (х) на частоту (f), или вес поделенной на сумму частот или весов.
х =
х =
3. Средняя гармоническая простая используется, когда произведения признака на частоту одинаковы или равны единице.
Хгарм. =
4. Средняя гармоническая взвешенная используется в случаях, когда известно значение произведения признака на частоту (хf), и значение признака (х), а частота не известна.
Х =
5. Средняя хронологическая равна сумме показателей ряда динамики, деленной на число показателей без одного, причем начальный и конечный уровни должны быть взяты в половинном размере.
Ххрон. = Мода и медиана Мода - это значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой - называется значение признаков, приходящихся на середину упорядоченной совокупности, т.е. в дискретном ряду необходимо просто найти эти величины без дополнительных расчетов.Мода и медиана дополняют расчеты средних величин и характеризуют структурное содержание дискретных и интервальных вариационных рядов, однако, как и средняя величина, мода и медиана не дают полного представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее.
Ряды распределения Ряд распределения - это упорядоченные по определенному варьирующемуся признаку однородные группы единиц совокупности. В зависимости от признака, положенного в основание построения ряда распределения, различают атрибутивные и вариационные ряды распределения. Атрибутивный ряд распределения - это ряд распределения, построенный по качественным признакам, не имеющим числового выражения и характеризующим свойство, качество изучаемого социально-экономического явления. Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволяют исследовать изменения структуры. Число групп атрибутивного ряда распределения адекватно числу градаций, разновидностей атрибутивного признака. Например, успевает или не успевает студент. Вариационный ряд распределения строится по количественному признаку. Любой такой ряд состоит из вариантов численных значений количественного признака, т.е. частоты (численности) отдельных вариантов или каждой группы вариационного ряда. Эти числа показывают, как часто встречаются те или иные варианты (значения признака) в ряду распределения. Сумма всех частот определяет численность всей совокупности. Дискретный вариационный ряд распределения - это ряд, в котором группы составлены по признаку, изменяющемуся дискретно и принимающему только целые значения. Интервальный вариационный ряд распределения - это ряд, в котором группировочный признак, составляющий основание группировки, может принимать в определенном интервале любые значения. Интервальный ряд распределения целесообразно строить, прежде всего, при непрерывной вариации признака, а также если дискретная вариация проявляется в широких пределах, т.е. число вариантов дискретного признака достаточно велико. Правила и принципы построения интервальных рядов распределения аналогичны правилам и принципам построения статистических группировок. Показатели вариации Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака, которые обусловлены перекрещивающимся влиянием действия различных факторов. Для характеристики размера вариации в статистике применяются абсолютные показатели вариации: размах вариации (с этим показателем вы частично познакомились ранее), который зависит только от величины крайних значений признака; среднее линейное отклонение; дисперсия и среднее квадратическое отклонение. Чтобы дать обобщающую характеристику распределения отклонений, рассчитывают, в первую очередь, среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности от среднеарифметической. Среднее линейное отклонение определяется как среднеарифметическое из отклонений индивидуальных значений от средней, без учета знака этих отклонений. Среднее линейное отклонение, как мера вариаций, признано применяемым в статистической практике крайне редко. Во многих случаях этот показатель не устанавливает степень рассеивания. На практике меру вариаций более обоснованно отражает показатель дисперсии (б2 - средний квадрат отклонений), рассчитанный Как средняя из отклонений, возведенный в квадрат: Дисперсия, как и среднее квадратическое отклонение б показывает на сколько в среднем отклоняются варианты от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения, б2 и б являются общепринятыми мерилами вариации признака. б-сигма
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

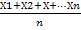
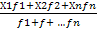
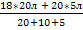
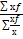 =
=