Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет скорости звука в газовой средеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для точного определения уровня жидкости в затрубном пространстве скважин и правильной интерпретации волнограмм (эхограмм) необходимо знать скорость распространения звуковой волны. Если принять во внимание, что скорость звуковой волны в газовой среде в реальных условиях скважины может изменяться от 250 м/сек до 420 м/сек, то очевидно, что ошибка в определении скорости звука может привести, и зачастую, к ошибкам в определении уровня жидкости до 40% от его фактического значения. Действительно, на практике нередки случаи, когда замеренный и рассчитанный, по принятой на месторождении зависимости скорости звука от давления, уровень оказывался ниже глубины спуска насоса. В других случаях за динамический уровень ошибочно принималось насосное оборудование скважины при отсутствии реального уровня жидкости (скважина работала газом). Таким образом, для правильного определения уровня жидкости в затрубном пространстве скважин необходимо точно знать скорость распространения импульса упругой волны или, что то же самое, скорость распространения звука
В настоящее время практически на всех месторождениях Западной Сибири для определения скорости звука применяют различные графические зависимости скорости звука Скорость распространения звуковой волны является функцией давления, температуры и состава газа. Состав газа в затрубном пространстве определяется термобарическими условиями на приеме насоса. Таким образом, даже на одной и той же скважине при различных режимах ее работы скорость распространения звуковой волны будет различной. Изучение распространения звука показало, что как гидродинамическое рассмотрение, так и учет релаксационных процессов приводят к следующему выражению для скорости звука в низкочастотном диапазоне [8]:
где
Скорость звука, определяемая по вышеприведенной формуле, является чисто термодинамической величиной, а распространение звука представляет собой адиабатический процесс. В результате проведенных преобразований данного выражения, проведенного в работе [14] получена формула для определения скорости звука в широком диапазоне давлений (от 0,1 до 40,0 МПа) и температур (от –50 до 2000С).
где
Для расчета основных термодинамических величин применяется уравнение состояние реальных газов Пенга-Робинсона [6].
Для расчета сжимаемости
где
Показатель адиабаты Изобарная теплоемкость определяется следующим образом:
где
Решая численно уравнение (8.9) методом конечных разностей и складывая полученный результат с уравнением (8.8) получаем изобарную емкость Изохорная теплоемкость определяется следующим образом [7]:
Частные производные По полученным зависимостям рассчитывается скорость звука для различной относительной плотности газа, приведенных давлений и температур. Для газовых смесей, незначительно отличающихся друг от друга по компонентному составу, можно определять скорость звука в непосредственных значениях давления и температуры. Проведенные расчеты по вышеизложенной методике показали, что для углеводородных газов с различным компонентным составом и незначительным содержанием азота N2 и окиси углерода СО2 скорость звука хорошо коррелируется с относительной плотностью газа
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.156.201 (0.009 с.) |

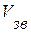 в газовой среде затрубного пространства скважин.
в газовой среде затрубного пространства скважин.
 , полученные экспериментальным путем, либо опубликованные в литературных источниках. Анализ различных методик по определению скорости звука привел к выводу, что точный расчет ее возможен только на основе решения основных термодинамических уравнений состояния реального газа.
, полученные экспериментальным путем, либо опубликованные в литературных источниках. Анализ различных методик по определению скорости звука привел к выводу, что точный расчет ее возможен только на основе решения основных термодинамических уравнений состояния реального газа.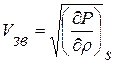 (8.3)
(8.3) - давление;
- давление;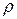 - плотность;
- плотность;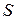 - энтропия.
- энтропия. (8.4)
(8.4)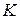 – показатель адиабаты;
– показатель адиабаты; – давление;
– давление; – сжимаемость газа;
– сжимаемость газа; – удельная газовая постоянная;
– удельная газовая постоянная;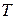 – абсолютная температура.
– абсолютная температура.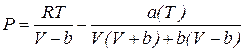 . (8.5)
. (8.5)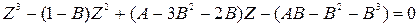 (8.6)
(8.6)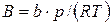 - коэффициент в уравнении (8.6);
- коэффициент в уравнении (8.6); ;
;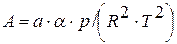 ;
; ;
;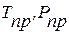 - приведенные значения температуры и давления;
- приведенные значения температуры и давления;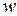 - ацентрический коэффициент.
- ацентрический коэффициент.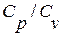 , где
, где 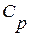 - изобарная теплоемкость,
- изобарная теплоемкость, 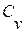 - изохорная теплоемкость.
- изохорная теплоемкость.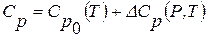 , (8.7)
, (8.7) - изобарная молярная теплоемкость идеальных газов, которая для смеси определяется как [9]:
- изобарная молярная теплоемкость идеальных газов, которая для смеси определяется как [9]: , (8.8)
, (8.8) - изотермическая поправка теплоемкости на давление, которая определяется как частная производная от приращения энтальпии по температуре при постоянном давлении:
- изотермическая поправка теплоемкости на давление, которая определяется как частная производная от приращения энтальпии по температуре при постоянном давлении: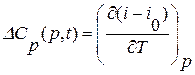 . (8.9)
. (8.9)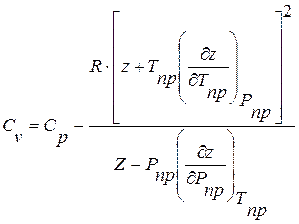 . (8.10)
. (8.10)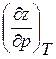 и
и  решаются численно методом конечных разностей.
решаются численно методом конечных разностей. ). На рис. 8.2, 8.3 представлены зависимости скорости звука от давления и температуры для относительной плотности газа 0,6 и 0,8 для смесей углеводородных газов.
). На рис. 8.2, 8.3 представлены зависимости скорости звука от давления и температуры для относительной плотности газа 0,6 и 0,8 для смесей углеводородных газов.