
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изохронный метод снятия индикаторных диаграммСодержание книги
Поиск на нашем сайте
(схема третья) Метод исследования скважин в течение равных интервалов времени – метод изохрон был впервые предложен в работе для исследования газовых скважин, эксплуатирующих пласты с низкой проницаемостью. Метод заключается в следующем. Скважина из установившегося состояния пускается в работу на время Т с дебитом q1, затем останавливается, и в момент 2Т пускается в работу с дебитом q2, далее в момент t=3Т останавливается и т.д. (см. рис. 5.1 (в)). При этом каждое новое значение давления, определенное в закрытой скважине, используется в расчете следующего испытания в качестве пластового давления. Основной принцип изохронного исследования заключается в том, что в процессе отдельных исследований на приток, проведенных в течение какого-то отрезка времени, будет дренироваться зона одного и того же радиуса Rк. Таким образом, здесь выполняется одно из основных условий исследования на установившихся режимах фильтрации – неизменность радиуса дренирования. Изменение депрессии в четные и нечетные промежутки времени в соответствующие моменты пуска и остановки по методу суперпозиции будет равно:
Согласно условиям изохронности обозначим:
Произведя соответствующие преобразования, получим:
где e – гидропроводность пласта; f0=æ×T/rc2 – параметр Фурье; qn – дебит циклов Здесь добавки к первым слагаемым в виде суммы
На основании этих значений строится зависимость Таким образом, коэффициент продуктивности по изохронному методу будет определен с некоторой погрешностью d, зависящей от соотношения дебитов
где hуст – коэффициент продуктивности на установившемся режиме hизохр – на изохронном режиме. Учитывая, что
где Т1 – время стабилизации режима, ч, Т – время исследования на изохронном режиме, ч. Время стабилизации Т1 можно определить по формуле 5.1 или принять Т1»0,5×Rк2/æ. Таким образом, строя индикаторную кривую Пример 1. По данным исследования скважина № 398 (месторождение Оленье) методом снятия КВД определены следующие параметры:
Задание: определить время стабилизации режима Решение: время стабилизации режима определим по формуле 5.1.
Пример 2. По данным исследования скважины № 24 Салымского месторождения на установившихся режимах фильтрации, табл. 5.2, построить ИЛ в координатах
Таблица 5.2 Результаты исследования скважины № 24 Салымского месторождения
Решение: 1. По данным, табл. 5.2, графы 2, 6, 7, 8, строим ИЛ в координатах 2. Учитывая все режимы (см. рис. 5.4 (а)), включая и режим с нулевым дебитом, проводим осредненную линию. В этом случае ИЛ представляет собой прямую линию, следовательно, в пласте реализуется линейный закон фильтрации.
3. Определим значение коэффициента продуктивности по тангенсу угла наклона ИЛ к оси дебитов: Учитывая разброс точек на графиках ИЛ, параметры уравнений 5.4 и 5.7 определим методом наименьших квадратов.
Для облегчения расчетов составим табл. 5.3. Таблица 5.3 Данные исследования скважины № 24 на режимах
Параметры уравнения 5.4 ИЛ в координатах
Коэффициент продуктивности есть обратное значение от величин
Уравнение фильтрации по линейному закону есть выражение:
Вычислим параметр
Коэффициент продуктивности
Уравнение фильтрации по линейному закону при известном пластовом давлении запишем в виде:
Пример 3. Используя результаты исследования скважины № 27 Салымского месторождения (см. табл. 5.4), построить ИЛ. Рассчитать коэффициенты Таблица 5.4 Результаты исследования скважины № 27 Салымского месторождения на режимах
Решение: 1. На основании данных граф 3, 9 таблицы 5.4, строим ИЛ в координатах
Для графического определения параметров Для ИЛ, рис 5.6 (а) – 1976 г., конечный участок чуть искривлен и, вообще говоря, можно было бы считать ее почти прямолинейной. Но при расчете параметра деформации Для расчета a по ИЛ рис. 5.6(б) – 1981 г., использованы следующие точки ИЛ:
Следующая перестроенная ИЛ рис. 5.6 (б) в координатах Для расчета коэффициента
Перестроенная ИЛ в координатах
Характер ИЛ (см. рис. 5.6 (б)), перестроенной в координатах 4. Кроме графического метода, параметры 5. Выбор параметров
Расчетные депрессии для каждого режима вычисляются по формулам: – для квадратичного закона имеем выражение
– для квадратичного закона с учетом параметра деформации в виде
6. Результаты вычислений параметров Как видно (см. табл. 5.5), параметрам I. д ля ИЛ на рис. 5.6 (а), II. для ИЛ на рис. 5.6 (б), III. д ля ИЛ на рис. 5.6 (в), Уравнениями притока жидкости для ИЛ на рис.5.6 (а, б), в являются: I. II. III. 7. Расчет коэффициента продуктивности
Рассчитанные коэффициенты продуктивности по трем ИЛ показывают, что наибольший из них получен при отсутствии деформации в призабойной зоне пласта. I – квадратичный закон фильтрации.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.55.25 (0.006 с.) |

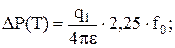
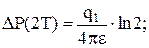
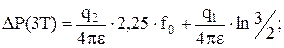 (5.37)
(5.37)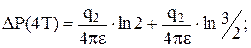
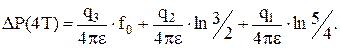
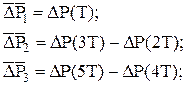 (5.38)
(5.38)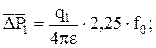
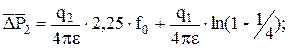
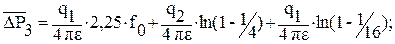 (5.39)
(5.39)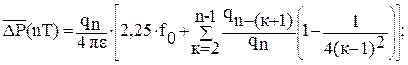
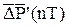 при
при 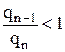 через 2-3 цикла быстро сходятся. Отбросив их, и обозначив
через 2-3 цикла быстро сходятся. Отбросив их, и обозначив 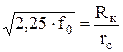 , получим:
, получим: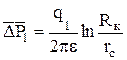 ;
; 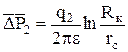 ;
; 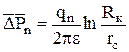 .
.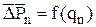 – индикаторная диаграмма.
– индикаторная диаграмма.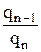 , количества циклов n и параметра Фурье f0=æ×T/rc2:
, количества циклов n и параметра Фурье f0=æ×T/rc2: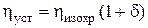 (5.40)
(5.40)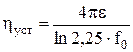 ;
;  , находим выражение для поправочного коэффициента:
, находим выражение для поправочного коэффициента: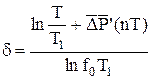 , (5.45)
, (5.45)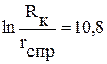 ;
; 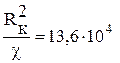 .
.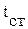 .
.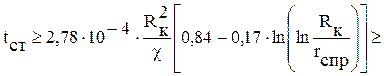
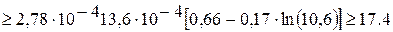 ч.
ч. 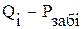 и
и 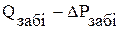 ,определить закон фильтрации и коэффициент продуктивности скважины.
,определить закон фильтрации и коэффициент продуктивности скважины.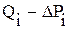 (см. рис. 5.4 (б)).
(см. рис. 5.4 (б)).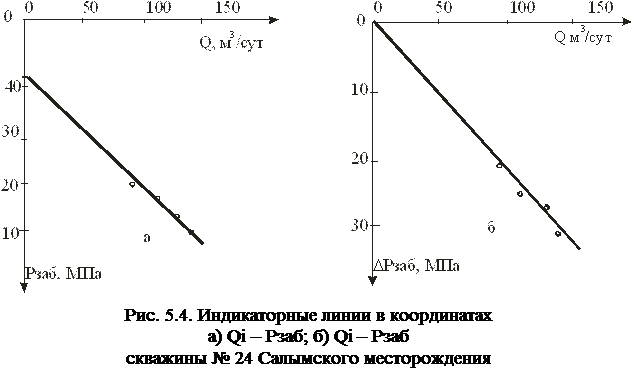
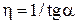 = 4,5 м3/сут×МПа.
= 4,5 м3/сут×МПа.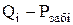 вычислим по формулам 5.5 и 5.6:
вычислим по формулам 5.5 и 5.6: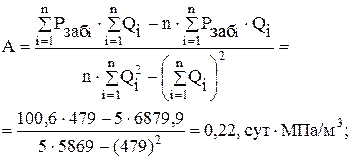
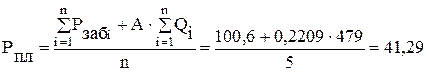 МПа.
МПа.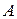 .
.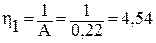 м3/сут×МПа.
м3/сут×МПа.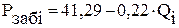 .
.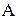 уравнения 5.7 по формуле 5.8:
уравнения 5.7 по формуле 5.8: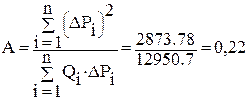 сут×МПа/м3.
сут×МПа/м3.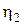 равен:
равен: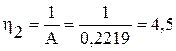 м3/сут×МПа.
м3/сут×МПа.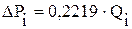 .
.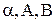 , записать уравнение притока жидкости в скважину.
, записать уравнение притока жидкости в скважину.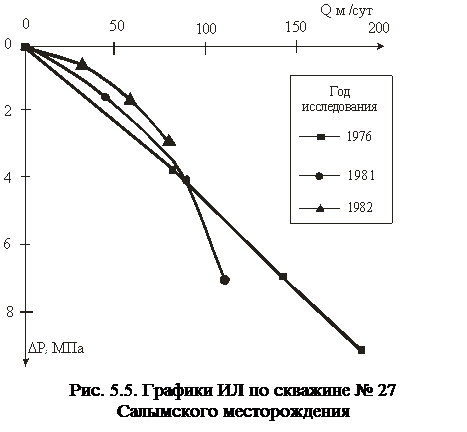
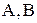 уравнений 5.9 и 5.12 ИЛ строятся в координатах
уравнений 5.9 и 5.12 ИЛ строятся в координатах 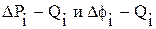 . Отметим, что ИЛ перестроенные в координатах
. Отметим, что ИЛ перестроенные в координатах 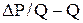 (см. рис. 5.6), имеют различный характер поведения.
(см. рис. 5.6), имеют различный характер поведения.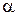 он получился равным
он получился равным 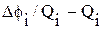 оказалась почти горизонтальной, что указывает на отсутствие или крайне незначительное влияние на фильтрацию жидкости инерционных сопротивлений.
оказалась почти горизонтальной, что указывает на отсутствие или крайне незначительное влияние на фильтрацию жидкости инерционных сопротивлений.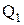 = 77 м3/сут,
= 77 м3/сут, 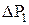 = 3,5 МПа;
= 3,5 МПа;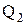 = 136 м3/сут,
= 136 м3/сут, 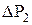 = 6,4 МПа;
= 6,4 МПа; = 187 м3/сут,
= 187 м3/сут, 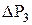 = 9,2 МПа.
= 9,2 МПа.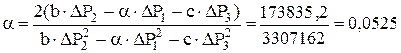 1/МПа;
1/МПа;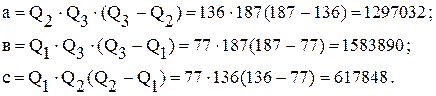
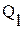 = 48 м3/сут,
= 48 м3/сут, 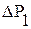 = 2,2 МПа;
= 2,2 МПа;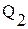 = 88,5 м3/сут,
= 88,5 м3/сут, 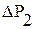 = 3,98 МПа;
= 3,98 МПа;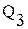 = 140 м3/сут,
= 140 м3/сут, 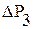 = 7,06 МПа.
= 7,06 МПа.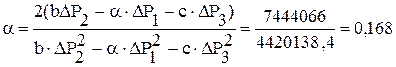 1/МПа
1/МПа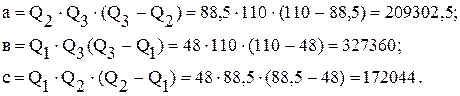
 практически прямолинейна (см. рис. 5.6 (б)).
практически прямолинейна (см. рис. 5.6 (б)).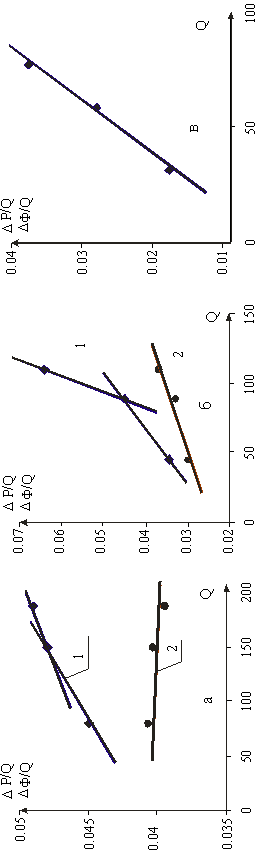
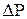 на
на 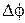 .
. между расчетной и фактической депрессиями:
между расчетной и фактической депрессиями: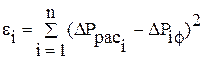 . (5.27)
. (5.27)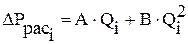 ; (5.28)
; (5.28)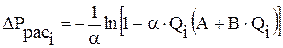 .
.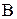 = 5×10-6;
= 5×10-6;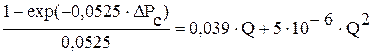 ;
;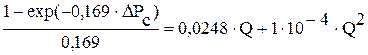 ;
;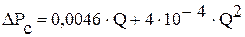 .
.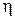 выполним для первого режима исследований.
выполним для первого режима исследований.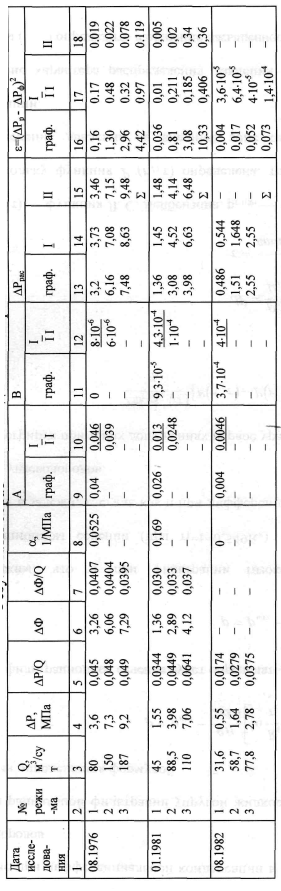
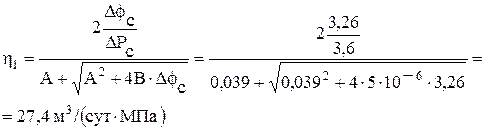
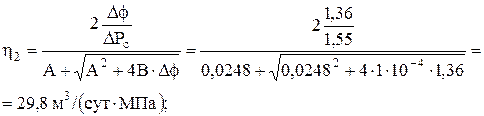
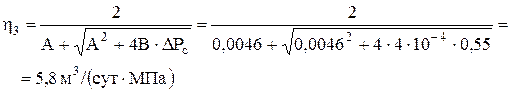 .
.


