Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка КВД горизонтальных скважинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для обработки КВД горизонтальных скважин предлагаются два метода: упрощенный метод Евченко и уточненный метод Бадри. По первому методу в основу обработки КВД положено приближенное уравнение притока:
которое при
где St вычисляется по формулам 13.2, 13.3. Последовательность расчета. 1. Проверяется условие 2. Если 3. По углу наклона асимптоты i вычисляют гидропроводность пласта k×h/m, а по точке пересечения асимптоты с осью абсцисс находят St. 4. Если При этом гидродинамические параметры k×h/m и St вычисляются аналогично вертикальным скважинам. Обработка кривых восстановления давления по уточненному методу Бадри [10]. Метод предусматривает идентифицировать режимы течения по форме графика КВД в координатах [ln(dDP(t)/dt) – lnt], обеспечивающие возможность предварительного определения гидродинамических параметров, характеризующих свойства продуктивного пласта. Анализ процессов идентификации режимов течения и оценка параметров требует необходимости определения профиля притока в скважину. Время начала и конца каждого режима течения зависит от проницаемости Кг и анизотропии c* пласта, эффективной длины горизонтального ствола и расстояний до кровли и подошвы пласта Z0. Согласно Бадри модель скважины с горизонтальным стволом и соответствующие режимы течения включают первый, второй и третий периоды радиального течения, а также промежуточные периоды линейных течений (см. рис.13.1). Последовательность расчета. 1. По результатам исследования строятся кривые зависимости в логарифмическом масштабе:
и производная изменения DР:
где t - время, обусловленное суперпозицией потоков до и после остановки скважины; Рс(ti) – восстановленное забойное давление после закрытия скважины;
Рс(tр) – давление на забой перед остановкой скважины; ti – время восстановления на забое; i - интервал отсчета. Первый период радиального течения идентифицируется по первому горизонтальному участку кривой [ln(dDP(t)/dt) – lnt] (см. рис.13.1). Определив угловой коэффициент i1 для прямолинейного участка кривой [ln(dDP(t)/dt) – lnt] (см. рис.13.2), рассчитывают гидропроводность пласта:
где Ку и Кz – проницаемости по оси Y и Z, мкм2; Lэф – эффективная (работающая) длина горизонтального ствола,м; q – дебит скважины перед закрытием ее на исследование, м3/сут; m - вязкость нефти, мПа×с. Второй период радиального течения наступает после окончания влияния кровли или подошвы пласта и может быть идентифицирован по второму горизонтальному участку кривой (см. рис.13.1). Угловой коэффициент i2 соответствующего прямолинейного участка кривой (рис.13.2) в два раза больше первого радиального течения. Тогда формула 13.12 запишется в виде:
Если длина горизонтального ствола намного превосходит толщину пласта (L >> h), то после окончания эффектов, связанных с кровлей и подошвой, может наступить промежуточный период линейного течения (см. рис.13.1). Этот период идентифицируется прямой с угловым коэффициентом i=0.5. Тогда
После второго линейного режима течения в плоскости горизонтального ствола развивается третий период радиального течения (см. рис.13.1). На графике в полулогарифмическом масштабе (см. рис.13.2) соответствующая прямая линия имеет угловой коэффициент i3. Тогда:
Идентификация режимов течения необходима для предварительной оценки параметров продуктивного пласта, которые впоследствии уточняются при сравнении фактических данных с расчетными. Если расстояние Zo от горизонтального ствола до границы известно, то можно определить проницаемость по напластованию (Кх×Ку) и перпендикулярное ему Кx. Формулы 13.12 и 13.13 позволяют определить параметр (Кх×Ку)×Lэф. Определив по формулам 13.12 и 13.13 вертикальные проницаемости Кz и принимая Кх = Ку, при известной длине горизонтального ствола по формулам 13.14 и 13.15 можно определить проницаемость вдоль напластования.
Принимая К=Кх=Ку, из формулы 13.12 нетрудно определить эффективную длину Lэф.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.5.216 (0.011 с.) |

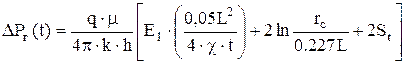 , (13.7)
, (13.7)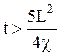 допускает логарифмическую аппроксимацию:
допускает логарифмическую аппроксимацию: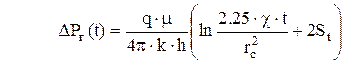 (13.8)
(13.8) .
.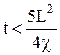 , то по данным исследования скважин строят график в координатах [DР(t) – E1(x)], где х = 0,05L2/ (4×c×t.)
, то по данным исследования скважин строят график в координатах [DР(t) – E1(x)], где х = 0,05L2/ (4×c×t.)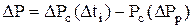 (13.9)
(13.9)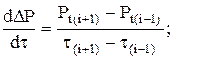 (13.10)
(13.10)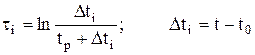 (13.11)
(13.11) tp – время работы скважины перед ее остановкой;
tp – время работы скважины перед ее остановкой; (13.12)
(13.12)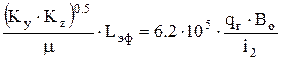 (13.13)
(13.13)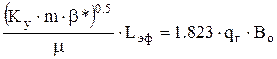 (13.14)
(13.14)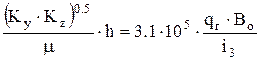 (13.15)
(13.15)